이 기사는 물리적 에너지의 교환을 나타내는 그래프에 관한 것이다. 2-버텍스 다중 그래프는 쌍극 그래프 를 참조하십시오. 본드 그래프 는 물리적 동적 시스템 을 그래픽 으로 표현한 것이다. 그것은 시스템을 주-공간 표현 으로 변환할 수 있게 한다. 이것은 블록 다이어그램 이나 신호 흐름 그래프 와 유사하며, 본드 그래프의 호는 물리적 에너지 의 양방향 교환을 나타내는 반면, 블록 다이어그램과 신호 흐름 그래프의 호는 단방향 정보 흐름을 나타낸다는 주요한 차이점이 있다. 본드 그래프는 다중 에너지 영역(예: 기계, 전기, 유압 등)과 도메인 중립이다. 이것은 결합 그래프가 여러 도메인을 원활하게 통합할 수 있다는 것을 의미한다.
본드 그래프는 "단일 포트", "이중 포트" 및 "다중 포트" 요소를 함께 연결하는 "본드"로 구성된다(자세한 내용은 아래 참조). 각 결합은 에너지의 순간 흐름 (dE /dt) 또는 동력 을 나타낸다. 각 결합의 흐름은 결합 변수 와 유사한 힘 변수라고 불리는 한 쌍의 변수에 의해 나타나는데, 그 변수의 생산물은 결합의 순간적인 힘이다. 권력 변수는 흐름과 노력의 두 부분으로 나뉜다. 예를 들어, 전기 시스템의 결합의 경우, 흐름은 전류인 반면, 노력은 전압이다. 이 예에서 전류와 전압을 곱하면 본드의 순간 전력을 얻을 수 있다.
본드에는 여기에서 간략하게 설명한 두 가지 다른 특징이 있으며, 아래에서 더 자세히 논의한다. 하나는 "반 화살" 사인 규약이다. 이것은 긍정적인 에너지 흐름의 가정된 방향을 정의한다. 전기 회로 다이어그램 및 자유체 다이어그램과 마찬가지로, 분석가가 선택한 정의와 일관성을 유지해야 한다는 주의와 함께 포지티브 방향의 선택은 임의적이다. 또 다른 특징은 "사유성"이다. 이것은 본드의 한쪽 끝에만 놓여 있는 수직 막대 입니다. 임의적인 것은 아니다. 아래에 기술한 바와 같이, 주어진 포트에 적절한 인과관계를 할당하는 규칙과, 포트 간 우선 순위에 대한 규칙이 있다. 인과관계는 노력과 흐름의 수학적 관계를 설명한다. 인과관계의 위치는 전력 변수 중 어느 것이 종속적이고 어떤 것이 독립적인지를 보여준다.
모델링할 물리적 시스템의 역학이 매우 다양한 시간 척도로 작동하는 경우, 고속 연속 시간 동작은 하이브리드 결합 그래프를 사용하여 순간 현상으로 모델링할 수 있다. 본드 그래프는 헨리 페인터 에 의해 발명되었다.[1]
본드 그래프용 시스템 많은 시스템은 본드 그래프에서 사용되는 용어로 표현될 수 있다. 이 용어들은 아래 표에 표현되어 있다.
아래 표에 대한 규칙:
P {\displaystyle P} 활성 전원 이며, X ^ {\ displaystyle {\hat{X}} x {\ displaystyle {\vec{x}} x † {\ displaystyle x^{\doger }}} 은둔자 임x 의 전치(transpose )의 복합 결합자임 . x 가 스칼라라면 은둔자는 복합 결합자와 같다. D t {\ displaystyle D_{t}^{n}}}} D t n f ( t ) = { ∫ − ∞ t f ( t ) d t , n < 0 f ( t ) , n = 0 ∂ n f ( t ) ∂ t n , n > 0 {\displaystyle D_{t}^{n}f(t)={\begin{cases}\displaystyle \int _{-\infty }^{t}f(t)\,dt,&n<0\\[2pt]f(t),&n=0\\[2pt]{\dfrac {\partial ^{n}f(t)}{\partial t^{n}}},&n>0\end{cases}}} { ⟨ x ⟩ α := x α sgn ( x ) ⟨ a ⟩ = k ⟨ b ⟩ β ⟹ ⟨ b ⟩ = ( 1 k ⟨ a ⟩ ) 1 / β {\displaystyle {\begin{cases}\langle x\rangle ^{\alpha }:= x ^{\alpha }\operatorname {sgn}(x)\\\langle {a}\rangle =k\langle b\rangle ^{\beta }\implies \langle b\rangle =\left({\frac {1}{k}}\langle a\rangle \right)^{1/\beta }\end{cases}}} Vergent-요인: ϕ L = { 프리즘의 : 길이 단면의 면적 실린더 : ln ( r a d i u s o u t r a d i u s i n ) 2 π ⋅ 길이 구 : 1 4 π ( r a d i u s i n ∥ − r a d i u s o u t ) {\displaystyle \phi _{L}={\begin{cases}{\textrm {Prismatic}}:\ {\dfrac {\textrm {length}}{{\textrm {cross-sectional}}\ {\textrm {area}}}}\\{\textrm {Cylinder}}:\ {\dfrac {\ln \left({\frac {\mathrm {radius_{out}} }{\mathrm {radius_{in}} }}\right)}{2\pi \cdot {\textrm {length}}}}\\{\textrm {Sphere}}:\ {\dfrac {1}{4\pi \left(\mathrm {radius_{in}} \par all \mathrm{-later_{out}}\right}}}\end{case}}} 일반화 흐름 일반화 변위 일반화 노력 일반화 운동량 일반화 전원(전력 시스템의 경우 와트 단위) 일반화된 에너지(전력 시스템의 경우 줄 단위 ) 이름 f → ( t ) {\displaystyle {\vec}{f}(t)} q → ( t ) {\displaystyle {\bec}{q}(t)} e → ( t ) {\displaystyle {\vec{e}(t)} p → ( t ) {\displaystyle {\vec}{p}(t)} P = f → ( t ) † e → ( t ) {\displaystyle P={\vec {f}(t)^{\daugger }{\vec {e}(t)} E = q → ( t ) † e → ( t ) {\displaystyle E={\vec{q}(t)^{\daugger }{\vec {e}(t)} 설명 변위시간파생성 정적 동작과 관련된 품질. 변위 단위당 에너지 노력의 시간적 요소 한 형태에서 다른 형태로 에너지의 변환 폐쇄형 시스템의 보존 수량 요소들 이름 하이퍼ance {\displaystyle H} 고압 H 1 {\ displaystyle H^{-1} 컴플라이언스 {\displaystyle C} 리지턴스 K C {\ displaystyle K=C^{-1} 저항 {\displaystyle R} 관성 I {\displaystyle I}( 또는 {\displaystyle }) Abrahance {\디스플레이 A} 돋보기 {\디스플레이 M} 특성. 전력 소산 요소 충전 저장 요소 (상태 변수: 변위)
(비용 변수: 노력)
전력 소산 요소 모멘텀 저장 요소 (상태 변수: 모멘텀)
(비용 변수: 흐름)
전력 소산 요소 전력 소산 요소 양적 행동 1차원 시스템(선형): P = H ⋅ ( D t 0 q ( t ) ) 2 {\displaystyle P=H\cdot \left(D_{t}^{0}q(t)\오른쪽)^{2}} 1차원 시스템의 경우:
e ( t ) = P γ [ D t − 1 q ( t ) ] [\displaystyle e(t)= P\gamma \left[D_{t}^{1}q(t)\right]}
임피던스:
Z ( s ) = 1 s 2 H = 1 s 2 P {\displaystyle Z={\frac {1}{s^{2} H}}={\frac{1}{s^{2}}P}
N-차원 시스템 을 위한 잠재적 에너지 : V = 1 2 q → ( t ) † e → ( t ) q → ( t ) = C ^ e → ( t ) {\displaystyle {\display{array}{lcl} V&=&#{\frac{1}{1}:{\vec{q}(t)^{\daugger }{\vec {e}(t)\\\vec{q}(t)&#{\c}{\vec}(t)&#{\c}{\vec}(t)\end{array}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 잠재적 에너지:
V = ∫ 0 q e ( q ) d q {\displaystyle V=\int _{0}^{q}e(q)\,dq}
잠재적 코에너지:
V ¯ = ∫ 0 e q ( e ) d e {\displaystyle {\overline{V}=\int_{0}^{e}q(e)de}
1차원 시스템의 경우:
f ( t ) = C ⋅ d e d t + e d C d t {\displaystyle f(t)=C\cdot {\frac {de}{dt}+e{\frac {dC}{dt}}}}
임피던스:
Z ( s ) = 1 s C = 1 s k {\displaystyle Z(s)={\frac {1}{sC}={\frac {1}{s}k} 속성: C {\displaystyle C} α {\displaystyle \alpha } 있는 , ( α displaystyle alpha )} , { e 2 = 1 2 e 2 D α C ( α ) f 2 = α ˙ {\displaystyle {\displaysty}e_{2}={\frac {1}{2}}e^{2} }D_{\alpha }C(\alpha )\\f_{2}={\dot{\alpha }}}}
1차원 시스템(선형): P = R ⋅ ( D t q ( t ) ) 2 {\displaystyle P=R\cdot \left(D_{t}q(t)\오른쪽)^{2}} 1차원 비선형 저항(e f {\displaystyle e(f)}
P = e ( f ) f (\displaystyle P=e(f)f}
Rayleigh Power:
R = 1 2 R ⋅ f ( t ) 2 {\displaystyle {\mathfrak {R}={\frac {1}{2}}R\cdot f(t)^{2}}
비선형 저항을 위한 Rayleigh Power:
R = ∫ 0 f e ( f ) d f {\displaystyle {\mathfrak{R}=\int _{0}^{f}e(f)\,df}
Rayleigh 노력:
e R = d R d f = e ( f ) {\displaystyle e_{\mathfrak{R}={\frac {d{\mathfrak{R}}{df}=e(f)}
N-차원 시스템의 경우:
P = f → ( t ) † e → ( t ) e → ( t ) = R ^ f → ( t ) {\displaystyle {\display{array}{lcr} P&={\vec {{f}(t)^{\dager}{\vec{e}(t)\\{\vec{e}(t)\{\vec{r}}{\vec{f}(t)\end{array}}}}}}}}}}
1차원 시스템의 경우:
e ( t ) = R ⋅ γ [ D t 1 q ( t ) ] [\displaystyle e(t)= R\cdot \gamma \left[D_{t}^{1}q(t)\right]}
임피던스:
Z ( s ) = R [\displaystyle Z(s)=] R}
N차원 시스템을 위한 운동 에너지 : T = 1 2 ρ → ( t ) † f → ( t ) ρ → ( t ) = L ^ f → ( t ) {\displaystyle {\display{array}{lcl} T={\frac{1}{2}}:{\vec{\rho }}^{\\dager }{\vec{f}}(t)\\\vec {f}(t)\\\\rho}={\hat {L}{\vec}(t)\c{f}}\array}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 운동 에너지:
T = ∫ 0 ρ f ( ρ ) d ρ {\displaystyle T=\int _{0}^{\rho }f(\rho )\,d\rho }
키네틱 코에너지:
T ¯ = ∫ 0 f ρ ( f ) d f {\displaystyle {\overline{T}=\int_{0}^{f}\rho(f)\,df}
1차원 시스템의 경우:
e ( t ) = L ⋅ d f d t + f ⋅ d L d t [\displaystyle e(t)= L\cdot {\frac {df}{dt}+f\cdot {\frac {dL}{dt}}}
임피던스:
Z ( s ) = s L [\displaystyle Z=sL} 속성: L {\displaystyle L} α {\displaystyle \alpha } 있는 , L ( displaystyle alpha )} { e 2 = 1 2 f 2 D α L ( α ) f 2 = α ˙ {\displaystyle {\displaysty}e_{2}={\frac {1}{2}}f^{2} }D_{\alpha }L(\alpha )\\f_{2}={\dot{\alpha }}}}
1차원 시스템(선형): P = A ⋅ ( D t 2 q ( t ) ) 2 {\displaystyle P=A\cdot \left(D_{t}^{2}q(t)\오른쪽)^{2}} 1차원 시스템의 경우:
e ( t ) = A ⋅ γ [ D t 3 q ( t ) ] [\displaystyle e(t)= A\cdot \gamma \left[D_{t}^{3}q(t)\right]}
임피던스
Z ( s ) = s 2 A {\displaystyle Z=s^{2} A}
1차원 시스템의 경우(선형) P = A ⋅ ( D t 3 q ( t ) ) 2 {\displaystyle P=A\cdot \left(D_{t}^{3}q(t)\오른쪽)^{2}} 1차원 시스템의 경우
e ( t ) = M ⋅ γ [ D t 5 q ( t ) ] [\displaystyle e(t)= M\cdot \gamma \left[D_{t}^{5}q(t)\right]}
임피던스
Z ( s ) = s 4 M {\displaystyle Z=s^{4} M}
자이터스 호환 Gyrator G 1초 1초 {\ displaystyle GY:{\frac }{s}k={\frac }{sc}}}} 저항성 G Y {\디스플레이 GY:r} Inertant Gyrator G Y s l {\displaystyle GY:sl} 양적 행동 방정식:
s c E 2 = F 1 ⟹ c D t e 2 + e 2 D t c = f 1 s c E 1 = F 2 ⟹ c D t e 1 + e 1 D t c = f 2 {\displaystyle {\begin{aigned}scE_{2}=F_{1}\implies cD_{t}e_{2}+e_{2} }D_{t}c=f_{1}\\scE_{1}=F_{2}\implies cD_{t}e_{1}+e_{1} }D_{T}c=f_{2}\end{aigned}}}}
흘러나오는 힘은 다음과 같이 흘러들어오는 힘과 같지 않다.
c e 1 D t e 2 + e 1 e 2 D t c = e 1 f 1 c e 2 D t e 1 + e 1 e 2 D t c = e 2 f 2 공통의 힘 = e 1 e 2 D t c {\displaystyle {\displaysty}ce_{1 }D_{t}e_{2}+e_{1}e_{1}e_{2}D_{t=e_{1}f_{1}f_{1}\cE_{2} }D_{t}e_{1}+e_{1}+e_{1}e_{2}d_{{t}c=e_{2}f_{2}\\{\textrm {Common}\{Common}\}\{\textrm {Power}=e_{1}D_{t}c\end{igned}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
속성 : c {\displaystyle c} ( 가 c ( displaystyle α {\ displaystyle (\alpha )}
{ e 3 = e 1 e 2 D α c ( α ) f 3 = α ˙ {\dot {\begin}e_{3}=e_{1}e_{1}e_{2}D_{\alpha }c(\alpha )\f_{3}={\dot{\alpha }}}}}}
방정식:
e 2 = r f 1 e 1 = r f 2 {\displaystyle {\signified}e_{2}=filename_{1}\e_{1}=filename_{2}\ended}}}}
흘러나오는 힘은 다음과 같다.
e 1 f 1 = e 2 f 2 {\displaystyle e_{1}f_{1}f_{1}=e_{2}f_{2}}:
방정식:
E 1 = s l F 2 ⟹ e 1 = l D t f 2 + f 2 D t l E 2 = s l F 1 ⟹ e 2 = l D t f 1 + f 1 D t l {\displaystyle {\reasoned} E_{1}=slF_{2}\implies e_{1}=lD_{t}f_{2}+f_{2} }D_{t}l\\ E_{2}=slF_{1}\implies e_{2}=lD_{t}f_{1}+f_{1} }D_{t}l\end{aigned}}}
흘러나오는 힘은 다음과 같이 흘러들어오는 힘과 같지 않다.
e 1 f 1 = l f 1 D t f 2 + f 1 f 2 D t l e 2 f 2 = l f 2 D t f 1 + f 1 f 2 D t l 공통의 힘 = f 1 f 2 D t l {\displaystyle {\displaysty}e_{1}f_{1}=lf_{1} }D_{t}f_{2}+f_{1}f_{1}f_{2}D_{t}l\\e_{2}f_{2}=lf_{2} }D_{t}f_{1}+f_{1}+f_{1}f_{2}D_{{t}l\\\\textrm {Common}\{Common}\{power}\ =f_{1}f_{2}l\end}}}}}}}}}}}
속성: l {\displaystyle l} α {\displaystyle \alpha } 있는 α {\displaystyle (\alpha )} ,
{ e 3 = f 1 f 2 D α l ( α ) f 3 = α ˙ {\dot {\begin}e_{3}=f_{1}f_{1}F_{2}D_{\alpha }l(\alpha )\f_{3}={\dot {\alpha }}}}}}
이는 유도 기계 에서 확인된다.
일반화 행동 활성 에너지 공급원의 에너지: W = ∫ 0 q source d q {\displaystyle W=\int _{0}^{q}{e_{\text{source}}\,dq} 라그랑지안 : L T ( V W {\displaystyle {\mathfrak{L}=T-(V-W)}
해밀턴어 : H = T V W {\displaystyle {\mathfrak {H}=T+(V-W)}
해밀턴의 노력: e H d hd q {\ dplaystyle e_{\mathfrak{H}}={\frac{d{\mathfrak{H}}{dq}}}}}}
라그랑비아의 노력: e L d l q {\ dplaystyle e_{\mathfrak{L}={\frac{d{\mathfrak{L}}{dq}}}}}}
수동적 노력: e L H d d d d f {\ dplaystyle e_{\mathfak{ }}={\frac {d}{d d}}}{df}}}}
전력 방정식: d L d d H t 0 {\dplaystyle {\d{ mathfrak{L}}{dt}+{d}+{d{\mathfrak{H}}{dt}}}=0}
노력 방정식: e L e H 0 {\displaystyle e_{\mathfrak {L}+e_{\mathfrak {H}=0}
라그랑기 방정식: e R e L e L {\ displaystyle e_{\mathfrak {R}+e_{\mathfrak }=e_{\mathfrak {L}}}}
해밀턴 방정식: e R e L H e H {\ displaystyle e_{\mathfrak {R}+e_{\mathfrak{ }=-e_{\mathfrak {H}}}
W {\ displaystyle {\overline {W} W {\displaystyle W} {\displaystyle S} S {\ displaystyle {\overline {S}}
W ¯ + W = S ⋅ S ¯ W ¯ = ∫ 0 S ¯ S ( S ¯ ) d S ¯ W = ∫ 0 S S ¯ ( S ) d S {\displaystyle{\begin{ligned}{\w}+S\cdot {\overline{S}\\\\overline{W}\\\overline{0}^{S}}}}\,d{\overline {S}\cdownline {S}\\\\\\} W=\int _{0}^{S}{\overline {S}(S)dS\end{arged}}}
선형 요소의 경우: W ' = W 1 2S ⋅ S '{\ displaystyle{\overline{W}=W={\frac{1}{2}}S\cdot{\overline{S}}}}
종방향 기계식 동력계통[2] 흐름 관련 변수 D 6 x {\displaystyle D_{t}^{6}x} m s 6 ] {\ displaystyle \mathrm {[m/s^{6}]}}} D 5 x {\displaystyle D_{t}^{5}x} m s 5 ] {\ displaystyle \mathrm {[m/s^{5}]}}} D 4 x {\displaystyle D_{t}^{4}x} s 4 ] {\ displaystyle \mathrm {[m/s^{4}]}}} D t 3 x {\displaystyle D_{t}^{3}x} Bull m / s3 ] {\ displaystyle \mathrm {[m/s^{3}]} } D t 2 x {\displaystyle D_{t}^{2}x} 가속 x 2 m s 2 ] {\ displaystyle (x_{2t})\\mathrm {[m/s^{2}]}}}}} D t 1 {\displaystyle D_{t}^{1}x} Velocity x t s ] {\ displaystyle (x_{t}}\mathrm {[m/s Flow) D t 0 x {\displaystyle D_{t}^{0}x} (x m ] {\ displaystyle (x)\\mathrm {[m 변위) D x {\displaystyle D_{t}^{-1}x} m ⋅ s ] {\ displaystyle \mathrm {[m\cdot ]} } D t x {\displaystyle D_{t}^{-2}x} m ⋅ s 2 ] {\ displaystyle \mathrm {[m\cdot ^{2}]} }} D t 3 displaystyle D_{t}^{-3}x m s s displaystyle \mathrm {[m\cdot ^{3}]}} } D x {\displaystyle D_{t}^{-4}x} [m ⋅ s 4 ] {\ displaystyle \mathrm {[m\cdot ^{4}]} }} 노력 관련 변수 D t 1 F {\displaystyle D_{t}^{1 }F} Yank [ ] {\ displaystyle \mathrm {[N/s]} } D t 0 F {\displaystyle D_{t}^{0 {} F } P x t N ] {\ displaystyle (P_{x}^{t})\\mathrm {[N]}}} Effort) D 1 F {\displaystyle D_{t}^{-1} F } 선형 운동량 (P x 2 k g ⋅ m / s] {\ displaystyle(P_{x}^{2t})\\\mathrm {[kg\cdot /s 모멘텀) 패시브 요소 준수(C) 저항(R) 관성(I) 아브라함스 (A) 돋보기(M) 봄 ⟨ P x t ⟩ = k ⟨ x ⟩ {\displaystyle \langle P_{x}^{t}\angle =k\langle x\angle } 여기서 k {\displaystyle k} 스프링 강성 이다. 댐퍼 ⟨ P x t ⟩ = b ⟨ x t ⟩ {\displaystyle \langle P_{x}^{t}\rangele =b\langle x_{t}\rangele } 여기서 b {\displaystyle b} 미사 ⟨ P x t ⟩ = m ⟨ x 2 t ⟩ {\displaystyle \langle P_{x}^{t}\rangele =m\langle x_{2t}\rangele } 여기 {\displaystyle m} 아브라함-로렌츠 힘
⟨ P x t ⟩ = μ 0 q 2 6 π c ⟨ x 3 t ⟩ {\displaystyle \langle P_{x}^{t}\angle ={\frac {\mu_{0}q^{0}}2}}:{6\pi c}}\langle x_{3t}\angle }}}}} 어디에,
μ 0 {\ displaystyle \mu _{0}} 투과성임 q [\displaystyle q} 충전기 c [\displaystyle c} 빛의 속도 다.자기복사반응력
⟨ P q t ⟩ = μ 0 q 2 R 24 π c 3 ⟨ x 5 t ⟩ {\displaystyle \langle P_{q}^{t}\angle ={\frac {\\mu_{0}q^{0}R}{24\pi c^{3}}\langle x_{5t}\angle }}}}} 어디에,
μ 0 {\ displaystyle \mu _{0}} 투과성임 q [\displaystyle q} 충전기 c [\displaystyle c} 빛의 속도 다. R {\displaystyle R} 자기 모멘트 의 반지름이다. 칸틸레버 ⟨ P x t ⟩ = 3 E I L 3 ⟨ x ⟩ {\displaystyle \langle P_{x}^{t}\rangele = {\frac {3 EI}{L^{3}}}\langle x\angle } L {\displaystyle L} E {\displaystyle E} 영의 계수 I {\displaystyle I} 번째 영역 모멘트 사이클로트론 방사선 저항
⟨ P x t ⟩ = σ t B 2 c μ 0 ⟨ x t ⟩ {\displaystyle \langle P_{x}^{t}\angle ={\frac {\\\sigma_{t}B^{2}}:{c\mu_{0}\langle x_{t}\angle }}}}}} 어디에,
σ t {\ displaystyle \sigma _{t} 톰프슨 단면 c [\displaystyle c} 빛의 속도 μ 0 {\ displaystyle \mu _{0} 투과성 B {\displaystyle B} 자기장 밀도 넓은 수역의 프리즘 플로터
⟨ P x t ⟩ = ρ L g A ⟨ x ⟩ {\displaystyle \langle P_{x}^{t}\rangle =\rho_{L}gA\langle x\rangle } 어디에,
ρ L {\ displaystyle \rho _{L} A {\displaystyle A} g {\displaystyle g} 비스코스 마찰 ⟨ P x t ⟩ = b ⟨ x t ⟩ {\displaystyle \langle P_{x}^{t}\rangele =b\langle x_{t}\rangele } 여기서 b {\displaystyle b} 탄성 로드 ⟨ P x t ⟩ = E A L ⟨ x ⟩ {\displaystyle \langle P_{x}^{t}\angle ={\frac {EA}{L}}\langle x\angle }} 어디에,
E {\displaystyle E} 영의 계수 A {\displaystyle A} L {\displaystyle L} 키네틱 모빌리티의 역행 ⟨ P x t ⟩ = 1 μ ⟨ x t ⟩ {\displaystyle \langle P_{x}^{t}\angle ={\frac {1}{\mu }}\langle x_{t}\angle }}} 여기서 μ[\displaystyle \mu } 뉴턴의 중력 법칙
⟨ P x t ⟩ = G M m ⟨ x ⟩ − 2 {\displaystyle \langle P_{x}^{t}\angle =GM\langle x\angle ^{-2}} 어디에,
G {\displaystyle G} 중력 상수 M {\displaystyle M} m {\displaystyle m} 공기와 상호 작용하는 지오메트리(예 : 드래그)
⟨ P x t ⟩ = 1 2 c ρ A ⟨ x t ⟩ 2 {\displaystyle \langle P_{x}^{t}\rangle ={\frac {1}{1}{2}}:c\rho A\langle x_{t}\rangle ^{2}}: 어디에,
A {\displaystyle A} c {\displaystyle c} ρ {\displaystyle \rho } 쿨롱의 법칙
⟨ P x t ⟩ = Q q 4 π ε 0 ⟨ x ⟩ − 2 {\displaystyle \langle P_{x}^{t}\angle ={\frac {Qq}{4\pi \varepsilon _{0}}\langle x\angle ^{-2}} 어디에,
ε 0 {\ displaystyle \varepsilon _{0} 허용률 Q {\displaystyle Q} q {\displaystyle q} 압스퀘어 댐퍼 ⟨ P x t ⟩ = B ⟨ x t ⟩ 2 {\displaystyle \langle P_{x}^{t}\rangele =B\langle x_{t}\rangele ^{2}} 여기서 B {\displaystyle B} 카시미르 포스
⟨ P x t ⟩ = A ℏ c π 2 240 ⟨ x ⟩ − 4 {\displaystyle \langle P_{x}^{t}\angle ={\frac {A\hbar c\pi ^{2}}:{240}\langle x\angle ^{-4}}} 어디에,
A {\displaystyle A} ℏ {\displaystyle \hbar } 플랑크의 축소 상수 c [\displaystyle c} 빛의 속도 드라이 마찰
⟨ P x t ⟩ = μ F n ⟨ x t ⟩ 0 {\displaystyle \langle P_{x}^{t}\angle =\mu F_{n}\langle x_{t}\angle ^{0}}}} 어디에,
μ [\displaystyle \mu } F n {\ displaystyle F_{n} 비오 사바트 법
⟨ P x t ⟩ = μ 0 I 1 I 2 l 2 π ⟨ x ⟩ − 1 {\displaystyle \langle P_{x}^{t}\angle ={\frac {\mu _{0} I_{1}I_{2}l}{2\pi }}}\langle x\angle ^{-1} 어디에,
μ 0 {\ displaystyle \mu _{0} 투과성 I 1 {\ displaystyle I_{1 I 2 {\ displaystyle I_{2 l {\displaystyle l} 피스톤이 단열실 내부의 오일을 누름
P x t = A P 0 ( 1 + x x 0 ) − γ {\displaystyle P_{x}^{t}= AP_{0}\좌측(1+{\frac {x}{x_{0}}\우측)^{-\gamma }}}} 어디에,
A {\displaystyle A} P 0 {\ displaystyle P_{0} x 0 {\ displaystyle x_{0} γ {\displaystyle \gamma }
전력계통 흐름 관련 변수 D t 2q {\displaystyle D_{t}^{2}q} / s] {\ displaystyle \mathrm {[A/s]}}} D t 1 q {\displaystyle D_{t}^{1 } 전류 q A displaystyle (q_{t}\\mathrm {[A 흐름) D t 0 q {\displaystyle D_{t}^{0}q} 전하 (q C ] {\ displaystyle (q)\\\mathrm {[C 교체) 노력 관련 변수 D 1 V {\displaystyle D_{t}^{1}V} V / s] {\ displaystyle \mathrm {[V/s]} } D t 0 V {\displaystyle D_{t}^{0}V} 전압 (Pq V ] {\ displaystyle (P_{q}^{t})\\\mathrm {[V Effort) D t − 1 V {\displaystyle D_{t}^{-1}V} Flux Linkage ( P q 2 t ) [ V ⋅ s ] or [ W b ⋅ t u r n ] {\displaystyle (P_{q}^{2t})\ \ \mathrm {[V\cdot s]} {\text{ or }}\mathrm {[Wb\cdot turn]} } (Momentum) 요소들 하이퍼랜스(H) 준수(C) 저항(R) 관성(I) 아브라함스 (A) 주파수 종속 음극 저항기(FDNR)
⟨ P q t ⟩ = 1 H ⟨ q t ⟩ {\displaystyle \langle P_{q}^{t}\rangle ={\frac {1}{{\frac H}}\langle q^{t}\angle }
선형 콘덴서
⟨ P q t ⟩ = 1 ε ϕ L ⟨ q ⟩ {\displaystyle \langle P_{q}^{t}\rangle ={\frac {1}{{\barepsilon }}\pi _{L}\langle q\rangle }}} 어디에,
ε {\displaystyle \varepsilon } 허용률 ϕ L {\ displaystyle \pi _{L} 선형 저항기
⟨ P q t ⟩ = ρ ϕ L ( 1 + α ( T − T 0 ) ) ⟨ q t ⟩ {\displaystyle \langle P_{q}^{t}\rangle =\rho \phi _{L}(1+\alpha(T-T_{0})\langle q_{t}\rangle }} 어디에,
ρ {\displaystyle \rho } ϕ L {\ displaystyle \pi _{L} α {\displaystyle \alpha } T {\displaystyle T} T 0 {\ displaystyle T_{0} 선형 인덕터 (솔레노이드)
⟨ P q t ⟩ = μ 0 N 2 A L ⟨ q 2 t ⟩ {\displaystyle \langle P_{q}^{t}\angle ={\frac {\mu _{0}N^{2} A}{{L}}\langle q_{2t}\angle } 어디에,
μ 0 {\ displaystyle \mu _{0} N {\displaystyle N} A {\displaystyle A} L {\displaystyle L} 주파수 종속 음전도(FDNC) 유형
γ 1 ⟺ V = R D t 2 i [ H ⋅ s ] {\displaystyle \gamma ^{1}\iff V=RD_{t}^{2}i\quad [H\cdot s]}
다이오드
P q t = n V T ln ( 1 + q t I s ) {\displaystyle P_{q}^{t}=nV_{{} T}\ln \left(1+{\frac {q_{t}}}}{{{t}}}}{{{n1}}}{ I_{s}}\오른쪽)} 어디에,
n {\displaystyle n} V {\ displaystyle V_{T} I s {\ displaystyle I_{s} 토로이드
⟨ P q t ⟩ = μ N 2 A 2 π r ⟨ q 2 t ⟩ {\displaystyle \langle P_{q}^{t}\angle ={\frac {\mu N^{2} A}{2\pi r}\langle q_{2t}\angle } 어디에,
μ [\displaystyle \mu } N {\displaystyle N} A {\displaystyle A} r {\displaystyle r} 인트라-가이레이터 인터지레이터 규준형 Gyrator 저항성 집광기 관성형 집광기 홀 효과 장치
e x = R H B z t z i y e y = R H B z t z i x {\displaystyle {\begin}e_{x}=R_{ H}{\frac{B_{z}}{t_{z}}i_{y}\e_{y}=R_{{}}{{z}}}i_{y}}}\e_{y}}=R_{{}}}{}}} H}{\frac{B_{z}}{t_{z}}i_{x}\end{arged}}}}} 어디에,
R H {\ displaystyle R_{ H}} B z {\ displaystyle B_{z} t z {\ displaystyle t_{z} 유도 모터
e r 1 = M cas ( θ ) D t f s 1 + f s 1 D t [ M cas ( θ ) ] e s 1 = M cas ( θ ) D t f r 1 + f r 1 D t [ M cas ( θ ) ] {\displaystyle {\begin{aligned}e_{r}^{1}=M\cos(\theta )D_{t}f_{s}^{1}+f_{s}^{1}D_{t}\left[M\cos(\theta )\right]\\e_{s}^{1}=M\cos(\theta )D_{t}f_{r}^{1}+f_{r}^{1}D_{t}\left[M\cos(\theta )\right]\end{aligned}}} 어디에,
θ {\displaystyle \theta} e r 1 {\ displaystyle e_{r}^{1}:{ e 1 {\ displaystyle e_{s}^{1}:{ f 1 {\ displaystyle f_{s}^{1}:{ f r 1 {\ displaystyle f_{r}^{1}:{ DC 모터
τ e = k a ϕ a ( i e ) i a ω e = 1 k a ϕ a ( i e ) e a {\displaystyle {\pregated}\tau _{e}}\phi _{a}i_{a}\\\omega _{e}={\frac {1}{k_{a}\pi _{a}(i_{e}) }}}{a}\end{aigned}}} 어디에,
τ e {\ displaystyle \tau _{e} Ω e {\ displaystyle \omega _{e} i e {\ displaystyle i_{e} i {\ displaystyle i_{a} 패러데이 집레이터
F = B l i V = 1 B l v {\displaystyle {\reasoned} F&=Bli\\ V&={\frac {1}{Bl}v\end{arged}} 어디에,
F {\displaystyle F} v {\displaystyle v} V {\displaystyle V} B {\displaystyle B} l {\displaystyle l} 패러데이 디스크
V = 1 2 B r 2 ω τ = 1 2 B r 2 i {\displaystyle {\reasoned} V&={\frac{1}{2}}:Br^{2}\omega \\tau &={\frac {1}{1}{2}}:Br^{2}i\ended}}}}}} 어디에,
B {\displaystyle B} r {\displaystyle r} 인트라포머 인터트랜스포머 전기 변압기(AC 신호 전용 )
V 2 = N 2 N 1 V 1 f 2 = N 1 N 2 f 1 {\displaystyle {\reasoned} V_{2}&={\frac {N_{1}:{1}V_{1}:{1}\\f_{2}&={\frac{{N_{1}:{1}}{{N_}}{1}:{1}}}{{1}}f_{1}}\ended}}}}}}}}}}}
유압/공압 전원 시스템 흐름 관련 변수 D t 1 V {\displaystyle D_{t}^{1}V} 체적 유량 (V t m 3 s ] {\ displaystyle(V_{t})\\mathrm {[m^{3}/s 흐름) D t 0 V {\displaystyle D_{t}^{0}V} 볼륨 (V m 3 ] {\ displaystyle(V)\\\mathrm {[m^{3 교체) 노력 관련 변수 D t P {\displaystyle D_{t}^{0}P} 압력 (PV a ] {\ displaystyle(P_{V}^{t}\\\mathrm {[Pa 에포트) D 1 P {\displaystyle D_{t}^{-1} P } P 2 t P a s ] {\ displaystyle (P_{V}^{2t})\\\mathrm {[Pa\cdodot ]}}}}}}}}}( Momentum) 요소들 준수(C) 저항(R) 관성(I) 파이프 탄력성
⟨ P V t ⟩ = ( t W E 2 r 0 V 0 ) ⟨ V ⟩ {\displaystyle \langle P_{V}^{t}\rangle =\왼쪽({\frac {t_{W}E}{2r_{0}V_{0}}\오른쪽)\langle V\rangle } 어디에,
r 0 {\ displaystyle r_{0} V 0 {\ displaystyle V_{0} T W {\ displaystyle t_{ W} E {\displaystyle E} 다아시 스펀지
⟨ P V t ⟩ = ( μ k ϕ L ) ⟨ V t ⟩ {\displaystyle \langle P_{V}^{t}\rangle =\좌측({\frac {}}{k}}\phi _{L}\오른쪽)\langle V_{t}\rangle }}} 어디에,
μ [\displaystyle \mu } k {\displaystyle k} 투과성 ϕ L {\ displaystyle \pi _{L} 파이프 내 유체 관성
⟨ P V t ⟩ = ( ρ ϕ L ) ⟨ V 2 t ⟩ {\displaystyle \langle P_{V}^{t}\angle =\왼쪽(\rho \phi_{L}\오른쪽)\langle V_{2t}\angle }} 어디에,
ρ {\displaystyle \rho } ϕ L {\ displaystyle \pi _{L} 압축 가능한 유체(대략)
⟨ P V t ⟩ = ( B V 0 ) ⟨ V ⟩ = ( ρ 0 c 2 V 0 ) ⏟ 어쿠스틱 근사치 ⟨ V ⟩ {\displaystyle \langle P_{V}^{t}\rangle =\left({\frac {B}{V_{0}}}\right)\langle V\rangle =\underbrace {\left({\frac {\rho _{0}c^{2}}{V_{0}}}\right)} _{\begin{array}{c}{\text{Acoustic}}\\{\text{Approximation}}\end{array}}\langle V\rangle } 어디에,
V 0 {\ displaystyle V_{0} B {\displaystyle B} ρ 0 {\ displaystyle \rho _{0 c {\displaystyle c} 밸브
⟨ P V t ⟩ = ( ρ 2 C d 2 A 0 2 ) ⟨ V t ⟩ 2 {\displaystyle \langle P_{V}^{t}\angle =\좌측({\frac {\rho }{2C_{d}^{2} A_{0}^{2}}}\오른쪽)\langle V_{t}\랑글 ^{2}}
C d {\ 디스플레이 C_{d} ρ {\displaystyle \rho } A {\ displaystyle A_{0} 영역 A 1 ] n 1 h 0 n 1 {\ textstyle A{{\frac 1}{[m]^{n-1}}\왼쪽(h+h_{0}\오른쪽 n-1}
P V t = ρ g h 0 [ ( 1 + n V A 1 [ m ] n − 1 h 0 n ) 1 / n − 1 ] {\displaystyle P_{V}^{t}=\rhogh_{0}\좌측[1+{\frac{nV}{A{\frac{1}{{1}{m]^{n-1}{0}^{n}}}}}\우측]^{1/n}-1\우측} 어디에,
h [\displaystyle h} h 0 {\ displaystyle h_{0} ρ {\displaystyle \rho } A {\displaystyle A} [ m ] n 1 {\ displaystyle [m]^{n-1} n {\displaystyle n} g {\displaystyle g} 사례 n 1 {\displaystyle n=1}( P V t = ρ g A V {\displaystyle P_{V}^{t}={\frac {\rho g}{{}}}{ A}V} 사례 n 0 {\displaystyle n=0}( P V t = ρ g h 0 ( e V A [ m ] − 1 ) {\displaystyle P_{V}^{t}=\rho gh_{0}\왼쪽(e^{\frac {V}{{V}}{ A[m]}-1\오른쪽)} 실린더의 포아세유 저항
⟨ P V t ⟩ = ( 8 μ L π R 4 ) ⟨ V t ⟩ {\displaystyle \langle P_{V}^{t}\rangle =\왼쪽({\frac {8\mu L}{\pi R^{4}}\오른쪽)\langle V_{t}\rangle }} 어디에,
μ [\displaystyle \mu } L {\displaystyle L} R {\displaystyle R} 등온실
⟨ P V t ⟩ = k ⟨ V t ⟩ − 1 {\displaystyle \langle P_{V}^{t}\angle =k\langle V_{t}\angle ^{-1} 여기서 k {\displaystyle k}
난류 저항
⟨ P V t ⟩ = a t ⟨ V t ⟩ 7 4 {\displaystyle \langle P_{V}^{t}\langle V_{t}\langle V_{t}\langle ^{\frac{7}{4}}}}}} 여기 {\ displaystyle a_{t}
압축성 유체
P V t = − B ln V {\displaystyle P_{V}^{t}=-B\ln V} 여기서 B {\displaystyle B}
노즐
⟨ P V t ⟩ = ρ 2 ( A 밖으로 2 ∥ − A 에 2 ) ⟨ V t ⟩ 2 {\displaystyle \langle P_{V}^{t}\\rho }{{\rho }{{\text{out}}^{2}\parallel -A_{\in}^{nect}\right)}}}\langle V_{{t}\rangele ^{2}}: 어디에,
ρ {\displaystyle \rho } A 아웃 {\ displaystyle A_{\text{out}} A in {\ displaystyle A_{\text{in}} 단방광
P V t = P V , 0 t ( 1 − V V 0 ) − γ {\displaystyle P_{V}^{t}=P_{V,0}^{t}\좌측(1-{\prac {V}{V_{0}}\우측)^{-\gamma }}}}}}}}}{-\gamma }}}}}}}} 어디에,
P V 0 t {\ displaystyle P_{V,0}^{t}} V 0 {\ displaystyle V_{0} γ {\displaystyle \gamma 체크 밸브
P V t = k ln ( 1 + V t V t , 0 ) {\displaystyle P_{V}^{t}=k\ln \left(1+{\frac{V_{t}}{V_{t}}}{V_{t}}}}\오른쪽)} 어디에,
k {\displaystyle k} V t 0 {\ displaystyle V_{t,0}
기타 시스템:
열역학 전력 시스템(흐름의 엔트로피 속도 및 노력은 온도) 전기화학 전원 시스템(흐름이란 화학적 활동이며 노력은 화학적 잠재력) 열화학 전력 시스템(흐름의 질량 속도 및 노력은 질량별 엔탈피) 거시경제적 환율제도(대체는 상품이고 노력은 상품당 가격) 미시경제 환율제(대체는 인구, 노력은 1인당 GDP) 사면체 주의 사면체는 노력과 흐름 사이의 전환을 그래픽으로 보여주는 사면체다. 인접한 이미지는 일반화된 형태로 4면체를 보여준다. 사면체는 에너지 영역에 따라 수정할 수 있다.
사면체 상태의 사면을 사용하면 사면체 상의 어떤 변수들 간에 수학적 관계를 찾을 수 있다. 이 작업은 다이어그램 주위의 화살표를 따르고 도중에 모든 상수를 곱하는 방식으로 수행된다. 예를 들어 일반화된 흐름과 일반화된 변위 사이의 관계를 찾으려면 f (t )q (t ) 방정식의 더 많은 예를 아래에서 볼 수 있다.
일반화된 변위와 일반화된 흐름 사이의 관계.
q ( t ) = ∫ f ( t ) d t q(t)=\int f(t)\,dt}
일반화된 흐름과 일반화된 노력 사이의 관계.
f ( t ) = 1 R ⋅ e ( t ) {\displaystyle f(t)={\frac {1}{R}\cdot e(t)}
일반화된 흐름과 일반화된 모멘텀 사이의 관계.
f ( t ) = 1 I ⋅ p ( t ) {\displaystyle f(t)={\frac {1}{ I}\cdot p(t)}
일반화된 운동량과 일반화된 노력 사이의 관계.
p ( t ) = ∫ e ( t ) d t [\displaystyle p(t)=\int e(t)\,dt}
일반화된 흐름과 일반화된 노력 사이의 관계, 상수 C를 포함한다.
e ( t ) = 1 C ∫ f ( t ) d t {\displaystyle e(t)={\frac {1}{C}\int f(t)\,dt}
에너지 영역을 전환할 때 모든 수학적 관계는 동일하게 유지되며, 기호만 변경된다. 이를 다음과 같은 예시로 알 수 있다.
변위와 속도 사이의 관계.
x ( t ) = ∫ v ( t ) d t [\displaystyle x(t)=\int v(t)\,dt}
전류와 전압의 관계, 이것을 옴의 법칙이라고 도 한다.
i ( t ) = 1 R V ( t ) {\displaystyle i(t)={\frac {1}{R}V(t)}
힘과 변위의 관계, 후크의 법칙이라고 도 한다. 이 방정식에서 음의 부호는 화살표가 본드 그래프를 가리키는 방식에 포함되기 때문에 삭제된다.
F ( t ) = k x ( t ) {\displaystyle F(t)=kx(t)}
전력계통의 경우 공명의 주파수에 대한 공식은 다음과 같다.
ω = 1 L C {\displaystyle \omega ={\sqrt {\frac {1}{ LC}}
전력밀도계통의 경우 공명파 속도의 공식은 다음과 같다.
c = 1 L C {\displaystyle c={\sqrt {\frac {1}{ LC}}
구성 요소들 엔진이 샤프트를 통해 바퀴에 연결되면 회전하는 기계영역에서 동력이 전달되고 있는데, 이는 노력과 흐름이 각각 토크(τ)와 각속도(Ω)라는 뜻이다. 단어 본드 그래프는 단어가 성분을 정의하는 본드 그래프를 향한 첫 번째 단계다. 단어 본드 그래프로, 이 시스템은 다음과 같이 보일 것이다.
엔진 − − − − − ω τ 바퀴를 돌리다 {\displaystyle{\text}\{\textstyle \tau}{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\texture{theel}}}}}}}}}} 반 화살표는 사인 규약을 제공하는 데 사용되므로 so 과 Ω 이 양수일 때 엔진이 작동하고 있는 경우 도표를 그린다. 엔진 − − − ⇁ ω τ 바퀴를 돌리다 {\displaystyle {\text{엔진}\;{\copset {\textstyle \tau}{\\\\\\\\\\\\\\\\\\\!\\\\\!\\\\!\\\!\\\\\!\!\!\!\!\!\!\!\!\!\!\!\! \!\ristarpoondown }}\;{\text{wheel}}} 이 시스템은 보다 일반적인 방법으로도 표현될 수 있다. 여기에는 단어 사용에서 같은 항목을 나타내는 기호로 바꾸는 것이 포함된다. 이 기호들은 위에서 설명한 대로 일반화된 형태에 기초한다. 엔진이 휠에 토크를 가함에 따라, 그것은 시스템의 노력의 원천으로 표현될 것이다. 휠은 시스템의 임피던스로 표시할 수 있다. 또한 토크와 각속도 기호는 떨어뜨려 일반화된 기호로 대체하여 노력과 흐름을 보장한다. 예에서는 필요하지 않지만, 공채에 번호를 매기는 것이 일반적이다. 단순화된 도표는 아래에서 볼 수 있다.
S e − − − ⇁ f 1 e 1 I {\displaystyle {S_{e}\;{\copset {\textstyle e_{1}{1}{\nderset {\textstyle f_{1}{1}{-\\\\\\\\\!\\\\\!\\\!\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rightharpoondown }}\;{\text{ I}}
노력이 항상 결합의 흐름 위에 있다는 것을 감안할 때, 관련 정보를 잃지 않고 노력과 흐름 기호를 완전히 떨어뜨리는 것도 가능하다. 다만 채권번호를 떨어뜨려서는 안 된다. 그 예는 아래에서 볼 수 있다.
S e − − − ⇁ 1 I {\displaystyle {S_{e}\;{\copset {\textstyle _{1}{1}{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\\\!\!\!\\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rightharpoondown }}\;{\text{ I}}
본드 번호는 나중에 본드 그래프에서 주-공간 방정식으로 변환할 때 중요할 것이다.
원소 연관성 직렬 연결 요소가 다음과 같은 동작을 갖는다고 가정해 보십시오.
e ( t ) = α g ( q ( t ) ) [\displaystyle e(t)=\display g(q(t)] } 여기 g {\displaystyle g(x)} α {\displaystyle } . 그렇다면 1-제곱에 이러한 유형의 요소가 많다고 가정해 보십시오. 그러면 접합부의 총 전압은 다음과 같다. e ( t ) = ( ∑ i α i ) g ( q ( t ) ) ⟹ α eq = ∑ i = 1 N α i {\displaystyle e(t)=\좌(\sum _{i}\alpha _{i}\{i}\오른쪽)g(q(t)\implies {\begin{array}{c}\hline \line \alpha \{\n}}}}
병렬연관 요소가 다음과 같은 동작을 갖는다고 가정해 보십시오.
e ( t ) = g ( α q ( t ) ) [\displaystyle e(t)=g(\displayq(t)] } 여기 g {\displaystyle g(x)} α {\displaystyle } . 그런 다음 0-분할에 이러한 유형의 요소가 많다고 가정해 보십시오. 그러면 다음과 같이 유효하다.
g − 1 ( e ( t ) ) = α i q i ( t ) ⟹ 1 α i g − 1 ( e ( t ) ) = q i ( t ) ⟹ ( ∑ i 1 α i ) g − 1 ( e ( t ) ) = q ( t ) ⟹ g ( g − 1 ( e ( t ) ) ) = g ( 1 ∑ i 1 α i q ( t ) ) ⟹ α eq = ∥ i = 1 N α i {\displaystyle g^{-1}\left(e(t)\right)=\alpha _{i}q_{i}(t)\implies {\frac {1}{\alpha _{i}}}g^{-1}(e(t))=q_{i}(t)\implies \left(\sum _{i}{\frac {1}{\alpha _{i}}}\right)g^{-1}(e(t))=q(t)\implies g(g^{-1}(e(t)))=g\left({\frac {1}{\sum _{i}{\frac {1}{\alpha _{i}}}}}q(t)\right)\implies {\begin{array}{ c }\hline \alpha _{\text{eq}}=\parallel _{i=1}^{N}\a lpha _{i}\\hline \end{array}}}
단일 좌현 요소 단일 포트 요소는 하나의 포트만 가질 수 있는 본드 그래프의 요소들이다.
소스 및 싱크 출처는 시스템 입력을 나타내는 요소다. 그것들은 노력을 투입하거나 시스템으로 흘러 들어갈 것이다. 그것들은 각각 노력이나 흐름을 위해 소문자 "e" 또는 "f"가 있는 대문자 "S"로 표시된다. 소스는 항상 화살이 원소를 향하도록 할 것이다. 선원의 예로는 모터(노력의 원천, 토크), 전압 소스(노력의 원천), 전류 소스(흐름의 원천)가 있다.
S e − − − ⇀ J 그리고 S f − − − ⇀ J {\displaystyle S_{e}\;{\overset {\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!}! \!\rstarpoonup \!\! \!}\\\J\qquad {\text{and}\qquad S_{f}\;{\copset {\textstyle }{\\textstyle {}{-\\\\\\\\\\textstyle}{-\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rstarpoonup \!\! \!}\\\J} 여기서 J 는 분기점을 나타낸다.
싱크대는 시스템의 출력을 나타내는 요소다. 그것들은 출처와 같은 방식으로 표현되지만, 화살표가 원소로부터 떨어져 있는 대신 원소를 가리키도록 한다.
J − − − ⇀ S e 그리고 J − − − ⇀ S f {\displaystyle J\;{\copset {\textstyle }{\underset {\\\\\\\\\\\\\\\\\\\\\\\\\! \!\rstarpoonup \!\! \!}\\S_{e}\qquad {\text{and}\qquad J\;{\copset {\textstyle }{\nderset{-\\\\\\textstyle }{-\\\\\\\\\\\\\!\!\\!\!\!\!\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rstarpoonup \!\! \!}\;\ S_{f}}
관성 관성 원소는 대문자 "나"로 표시되며, 그 안에 항상 힘이 흐른다. 관성 원소는 에너지를 저장하는 원소다. 가장 일반적으로 이 질량은 기계 시스템을 위한 질량이고 전기 시스템을 위한 인덕터다.
J − − − ⇀ I {\displaystyle J\;{\copset {\textstyle }{\underset {\\\\\\\\\\\\\\\\\\\\\\\\\! \!\rstarpoonup \!\! \!}\\;\ I}
저항 저항 요소는 수도 "R"에 의해 표시되며, 항상 그 안으로 힘이 흐른다. 저항 원소는 에너지를 발산하는 원소다. 가장 일반적으로 이러한 것들은 기계 시스템용 댐퍼와 전기 시스템용 저항기들이다.
J − − − ⇀ R {\displaystyle J\;{\copset {\textstyle }{\underset {\\\\\\\\\\\\\\\\\\\\\\\\\! \!\rstarpoonup \!\! \!}\\;\ R}
준수 준수 요소는 대문자 "C"로 표시되며, 항상 그 안에 힘이 흐른다. 준수 요소는 잠재적 에너지를 저장하는 요소들이다. 가장 일반적으로 이러한 것들은 기계 시스템을 위한 스프링과 전기 시스템을 위한 콘덴서들이다.
J − − − ⇀ C {\displaystyle J\;{\copset {\textstyle }{\underset {\\\\\\\\\\\\\\\\\\\\\\\\\! \!\rstarpoonup \!\! \!}\\;\ C}
2포트 요소 이 원소에는 두 개의 포트가 있다. 그것들은 시스템 사이 또는 시스템 내에서 동력을 변화시키기 위해 사용된다. 하나에서 다른 하나로 변환할 때, 전송하는 동안 전원이 손실되지 않는다. 원소에는 그것과 함께 주어질 상수가 있다. 상수는 사용 중인 요소에 따라 변압기 상수 또는 집압기 상수라고 한다. 이러한 상수는 일반적으로 요소 아래의 비율로 표시된다.
변압기 변압기는 흐름의 흐름과 노력 사이의 관계를 적용한다. 예로는 이상적인 전기 변압기 나 레버 가 있다.
표시됨
− − − ⇀ 1 T R − − − ⇀ 2 r : 1 {\displaystyle {\displaystyle{\cHB}{\\textstyle _{1}{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\! \!\hightarpoonup }}\\\\TR\\\\\\\\\\{2}}:\nderset{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\\\\\\\\\\\!\!\!\!\!\\!\\\\\!\!\\\\\\\\\\\\\\!\! \!\rightharpoonup }}\\\\^{r:1}}\end{nd}}}} 여기 서 r은 변압기의 계수를 나타낸다. 이 말은 f 1 r = f 2 {\displaystyle f_{1}r=f_{2}} 그리고 e 2 r = e 1 {\displaystyle e_{2}r=e_{1}}
집레이터 집게이터 는 노력의 흐름과 흐름의 노력 사이에 관계를 적용한다. 집전기의 예로는 전압(전기적 힘)을 각도 속도(사각형 기계적 흐름)로 변환하는 DC 모터가 있다.
− − − ⇀ 1 G Y − − − ⇀ 2 g : 1 {\displaystyle {\displaystyle{\cHB}{\\textstyle _{1}{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\! \!\hightharpoonup }}\\\ GY\\\\\\\\\\\{2}}:\nderset {\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\\\\\\\!\!\\!\\!\!\!\!\\!\!\!\!\!\!\!\!\!\!\! \!\rightharpoonup }}\\\\^{g:1}}\end{nd}}} 라는 뜻 e 2 = g f 1 {\displaystyle e_{2}=gf_{1}} 그리고 e 1 = g f 2 . {\displaystyle e_{1}=gf_{2}. }
다중 포트 요소 다른 요소와 달리 결합은 내부 또는 외부로 임의의 수의 포트를 가질 수 있다. 접선은 그들의 항구에 전력을 분산시킨다. 노력과 흐름이 어떻게 전달되는가에 있어서만 다른 두 개의 뚜렷한 결합, 즉 0-접합과 1-접합이 있다. 직렬로 된 동일한 접합부는 결합할 수 있지만 직렬로 된 다른 접합부는 결합할 수 없다.
0-준수 0준수는 모든 노력 값(및 시간 적분/시간 적분)이 결합 전체에서 같도록 행동하지만, 흐름 값의 합은 흐름 값의 합계 또는 동등하게 모든 흐름의 합이 0이 되도록 작용한다. 전기 회로에서, 0 정합은 노드로서 해당 노드의 모든 구성 요소에 의해 공유되는 전압을 나타낸다. 기계적 회로에서, 0-접합은 구성 요소들 사이의 결합이며, 구성 요소에 연결된 모든 구성 요소가 공유하는 힘을 나타낸다.
전부 e 가 동일하다 {\displaystyle {\text{all}e{\text{s}s are equal}}} ∑ f 에 = ∑ f 밖으로 {\displaystyle \sum f_{\text{in}=\sum f_{\text{out}}}
예는 아래와 같다.
− − − ⇁ 1 0 ↾ 2 − − − ⇁ 3 {\displaystyle {\copset {\textstyle _{1}{\\\\\\\\\\\\\\\\! \!\rightharpoondown }}{\stackrel {\textstyle {\stackrel {\textstyle }{{2}}:{{\textstyle _{3}{\}{-\\\textstyleet {}{-\\\\\\\\!\\\\\\\\!\\\\!\\\\\\\\\\\\\\\\\\\\\\\!\\\\\\\\\!\\\\!\!\!\!\ \!\r8ardpoondown }}}}}
결과 방정식:
e 1 = e 2 = e 3 {\displaystyle e_{1}=e_{2}=e_{3}}} f 1 = f 2 + f 3 {\displaystyle f_{1}=f_{2}+f_{3} }}
6분의 1 1-제곱은 0-제곱과 반대로 작용한다. 1-제곱은 모든 흐름 값(및 시간 적분/제곱)이 결합 전체에서 동일하도록 작용하지만, 노력 값의 합은 모든 노력 값의 합계 또는 동등하게 0이다. 전기 회로에서, 1 접합부는 구성 요소 사이의 직렬 연결을 나타낸다. 기계적 회로에서, 1-제곱은 그것에 연결된 모든 구성 요소에 의해 공유되는 속도를 나타낸다.
전부 f 가 동일하다 {\displaystyle {\text{all}f{\text{s}s are equal}}} ∑ e 에 = ∑ e 밖으로 {\displaystyle \sum e_{\text{in}=\sum e_{\text{out}}}
예는 아래와 같다.
− − − ⇁ 1 1 ↾ 2 − − − ⇁ 3 {\displaystyle {\copset {\textstyle _{1}{\\\\\\\\\\\\\\\\! \!\rightharpoondown}}{\stackrel {\textstyle {\stackrel {\textstyle _{2}}:{{}{\textstyle _{3}{\}{\\textstyle {}{-\\\\\\\\textstyleet}\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\r8ardpoondown }}}}}
결과 방정식:
f 1 = f 2 = f 3 {\displaystyle f_{1}=f_{2}=f_{3}}} e 1 = e 2 + e 3 {\displaystyle e_{1}=e_{2}+e_{3 }}
인과성 본드 그래프는 본드의 어느 쪽이 순간적인 노력을 결정하고 그 순간적인 흐름을 결정하는지를 나타내는 인과성의 개념을 가지고 있다. 시스템을 설명하는 동적 방정식을 작성할 때, 인과관계는 각 모델링 요소에 대해 어떤 변수가 종속적이고 어떤 변수가 독립적일지를 정의한다. 한 모델링 요소에서 다른 모델링 요소로 그래픽으로 인과관계를 전파함으로써 대규모 모델의 분석이 쉬워진다. 본드 그래프 모델에서 인과 배정을 완료하면 대수적 루프가 존재하는 모델링 상황의 탐지가 가능할 것이다. 그것은 변수가 그 자체의 함수로 재귀적으로 정의되는 상황이다.
인과관계의 예로서 배터리와 직렬로 된 콘덴서를 고려한다. 즉석에서 캐패시터를 충전하는 것은 물리적으로 불가능하므로, 캐패시터와 병렬로 연결된 것은 반드시 캐패시터 전체에 걸쳐서와 동일한 전압(에포트 변수)을 가져야 한다. 마찬가지로, 인덕터는 즉시 플럭스를 변경할 수 없으므로 인덕터와 직렬로 된 모든 구성품은 반드시 인덕터와 동일한 흐름을 가질 것이다. 캐패시터와 인덕터는 패시브 장치이기 때문에 각각의 전압과 흐름을 무한정 유지할 수 없다. 즉, 캐패시터와 인덕터는 각각의 전압과 흐름에 영향을 미치지만 각각 전류와 전압에 영향을 줌으로써 간접적으로만 영향을 미친다.
참고: 인과관계는 대칭관계다. 한쪽이 노력을 "원인"하면 다른 한쪽은 "원인"이 흐른다.
본드 그래프 표기법에서, 힘 본드의 한쪽 끝에 인과 스트로크를 추가하여 반대쪽 끝이 노력을 정의하고 있음을 나타낼 수 있다. 휠을 구동하는 상시 토크 모터, 즉 노력의 원천(SE )을 고려하십시오. 그것은 다음과 같이 그려질 것이다.
모터를 달다 S E − − − ⇀ ω τ 바퀴를 돌리다 {\displaystyle {\displaysty}{r}{\text{data}\\\ SE\end{array}\;{\coverset {\textstyle \tau}{\underset {\textstyle \omega}{-\!\!\!\!\\\\!\\\\!\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rstarpoonup \!\! \!}}\;{\text{wheel}}}
대칭적으로 인과 스트로크가 있는 쪽(이 경우 휠)은 결합에 대한 흐름을 정의한다.
인과관계는 호환성 제약을 초래한다. 분명히 파워 본드의 한쪽 끝만이 노력을 정의할 수 있고 따라서 결합의 한쪽 끝만이 인과적 뇌졸중을 일으킬 수 있다. 또한 시간에 의존하는 행동을 가진 두 개의 수동적 요소인 I 와 C 는 오직 하나의 종류의 인과만을 가질 수 있다: I 요소 는 흐름을 결정한다; C 요소 는 노력을 정의한다. 따라서 접합부 J 에서 선호되는 인과 방향은 다음과 같다.
J − − − ⇀ I 그리고 J − − − ⇀ C {\displaystyle J\;{\copset {\textstyle }{\underset {\\\\\\\\\\\\\\\\\\\\\\\\\! \!\rstarpoonup \!\! \! }}}\; I\qquad {\text{and}\qquad J\;{\overset {\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rstarpoonup }}}\; C}
이러한 원소들이 선호하는 방법인 이유는 4면체에서 나타낼 방정식을 고려한다면 더욱 분석될 수 있다.
f ( t ) = 1 I ∫ e ( t ) d t 그리고 e ( t ) = 1 C ∫ f ( t ) d t {\displaystyle f(t)={\frac {1}{ I}}\int e(t)\,dt\qquad {\text{and}\\qquad e(t)={\frac {1}{C}\int f(t)\,dt}
결과 방정식은 독립적 전력 변수의 적분을 포함한다. 이것은 인과관계를 반대로 해서 파생되는 결과보다 선호된다. 그 방정식은 아래에서 볼 수 있다.
e ( t ) = I f ˙ ( t ) 그리고 f ( t ) = C e ˙ ( t ) [\displaystyle e(t)= I{\dot{f}(t)\qquad {\text{and}}\qquad f(t)= C{\dot{e}(t)}
본드 그래프는 선호되지 않는 방식으로 이러한 요소들 중 하나에 인과 바가 있을 수 있다. 이 경우 그 채권에서 '경계 갈등'이 발생했다고 한다. 인과 충돌의 결과는 그래프의 상태-공간 방정식을 작성할 때만 나타난다. 그것은 그 절에서 더 자세히 설명되어 있다.
저항기는 시간에 의존하는 동작이 없다: 전압을 인가하여 즉시 흐름을 얻거나, 흐름을 적용하여 전압을 즉시 얻는다. 따라서 저항기는 인과 결합의 어느 한쪽 끝에 있을 수 있다.
J − − − ⇀ R 그리고 J − − − ⇀ R {\displaystyle J\;{\copset {\textstyle }{\underset {\\\\\\\\\\\\\\\\\\\\\\\\\! \!\rstarpoonup \!\! \!}}}\;R\qquad {\text{and}\qquad J\;{\copset {\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\\\\!\!\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\ \!\rstarpoonup }}}\; R}
흐름의 원천(SF) 은 흐름을 정의하고, 노력의 원천(SE )은 노력을 정의한다. 트랜스포머는 수동적이며, 에너지를 발산하거나 저장하지 않으므로 인과관계는 다음과 같이 트랜스포머를 통과한다.
− − − − − T F − − − − − 또는 − − − − − T F − − − − − {\displaystyle \;{\copset {\textstyle }{-\\\\\\\\\\\\\\\\\\\\\\\\\}\\\; TF\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\! }}}\;\qquad {\text{or}}\qquad \;{\overset {\textstyle }{\underset {\textstyle }{ \!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-}}}\; TF\;{\copset{\textstyle }{\underset {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\}}
Gyrator는 흐름을 흐르려는 노력과 노력으로 변환하기 때문에 한쪽에서 흐를 경우 다른 쪽에서는 노력을 하고 그 반대쪽에서는 노력을 한다.
− − − − − G Y − − − − − 또는 − − − − − G Y − − − − − {\displaystyle \;{\copset {\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!}\; GY\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\! }}}\;\qquad {\text{or}}\qquad \;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\! }}}\; GY\;{\copset {\textstyle }{\underset {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\}
결합체 0분위에서는 노력이 평등하고, 1분위에서는 흐름이 평등하다. 따라서 인과적 결합을 가진 경우, 오직 하나의 결합만이 0분할에 노력을 야기할 수 있고, 오직 하나의 결합만이 1분할에 흐름을 유발할 수 있다. 따라서 하나의 접합부의 인과관계가 알려지면 다른 결합의 인과관계도 알려지게 된다. 그 하나의 채권은 '강력한 채권'이라고 불린다.
강한 유대감 → ⊣ 0 ⊥ ⊤ ⊣ 그리고 강한 유대감 → ⊢ 1 ⊤ ⊥ ⊢ {\displaystyle {\text{strong bond}\\오른쪽 화살표 \\cHB \\\textstyle \}{0}\\cHB \qquad{\textand}\text}\cHB}\rightarrow \;\vdash \! {\overset {\textstyle \bot }{\deset {\textstyle \top }{1}}\! \vdash }
인과관계 결정 본드 그래프의 인과관계를 판단하기 위해서는 특정 단계를 따라야 한다. 이러한 단계는 다음과 같다.
소스 인과 막대 그리기 C 및 I 본드에 대한 선호 인과관계 그리기 0 및 1 접합부, 변압기 및 자이지레이터에 대한 원인 막대 그리기 R 결합 인과 막대 그리기 인과 충돌이 발생하는 경우 C 또는 I 결합을 차별화로 변경하십시오. 아래에는 단계별 보행로가 나와 있다.
S f − − − ⇀ 0 − − − ⇀ T R − − − ⇀ 0 − − − ⇀ C 5 ⇃ r : 1 ⇃ C 2 R 6 {\displaystyle {\begin}S_{f}&#\overset {\textstyle {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\hightarpoonup }}&#{\copset{\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rstarpoonup }}& TR&{\cHBFFF{\textstyle}{\underset{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ \!\hightarpoonup }}&#{\copset{\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rightharpoonup }}}&c_{5}\&\downharpoonleft &&^{r:1}}&#{r:1}}&#&#&#&#>{2}&C_{6}&&R_&\end{matrix}}}}}}}}}}}}}}
첫 번째 단계는 출처에 대한 인과관계를 그리는 것인데, 그 위에 오직 한 가지뿐입니다. 이것은 아래 그래프를 나타낸다.
S f − − − ⇀ 0 − − − ⇀ T R − − − ⇀ 0 − − − ⇀ C 5 ⇃ r : 1 ⇃ C 2 R 6 {\displaystyle {\begin}S_{f}&#\overset {\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\hightarpoonup }}&#{\copset{\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rstarpoonup }}& TR&{\cHBFFF{\textstyle}{\underset{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ \!\hightarpoonup }}&#{\copset{\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rightharpoonup }}}&c_{5}\&\downharpoonleft &&^{r:1}}&#{r:1}}&#&#&#&#>{2}&C_{6}&&R_&\end{matrix}}}}}}}}}}}}}}
다음 단계는 C 채권에 대해 선호하는 인과관계를 그리는 것이다.
S f − − − ⇀ 0 − − − ⇀ T R − − − ⇀ 0 − − − ⇀ C 5 ⇃ ¯ r : 1 ⇃ C 2 R 6 {\displaystyle {\begin}S_{f}&#\overset {\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\hightarpoonup }}&#{\copset{\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rstarpoonup }}& TR&{\cHBFFF{\textstyle}{\underset{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ \!\hightarpoonup }}&#{\copset{\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rstarpoonup }}&c_{5}\&#\\bar{\downharpoon왼쪽 }}{{r:1}}&^{r:1}}&\\downharpoon 왼쪽 &>&c_{2}&&r_{6}&#&#&##{matrix}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
다음으로 0과 1 접합부, 변압기 및 자이터에 인과관계를 적용한다.
S f − − − ⇀ 0 − − − ⇀ T R − − − ⇀ 0 − − − ⇀ C 5 ⇃ ¯ r : 1 ⇃ _ C 2 R 6 {\displaystyle {\begin}S_{f}&#\overset {\textstyle {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\hightarpoonup }}&#{\copset{\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rstarpoonup }}& TR&{\cHBFFF{\textstyle}{\underset{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ \!\hightarpoonup }}&#{\copset{\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rstharpoonup }}&c_{5}\&#{\bar}{{\downharpoonleft }{r:1}}&^{r:1}}&#&#{\downharpoonleft }&#&#&c_{2}&R_{6}>end{matrix}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}?
그러나 왼쪽에는 0정맥의 문제가 있다. 0준동은 접속부에 두 개의 인과 바가 있지만, 0준동은 접속부에 한 개와 한 개만을 원한다. 이는 C 2 {\ textstyle C_{2 이 문제를 해결하는 유일한 방법은 그 인과관계의 막대를 뒤집는 것이다. 이로 인해 인과 충돌이 발생하며, 그래프의 수정 버전은 아래와 같으며, {\textstyle \star}
S f − − − ⇀ 0 − − − ⇀ T R − − − ⇀ 0 − − − ⇀ C 5 ⇃ _ ⋆ r : 1 ⇃ _ C 2 R 6 {\displaystyle {\begin}S_{f}&#\overset {\textstyle {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\hightarpoonup }}&#{\copset{\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\! \!\rstarpoonup }}& TR&{\cHBFFF{\textstyle}{\underset{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ \!\hightarpoonup }}&#{\copset{\textstyle }{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\!\!\!\!\!\!\!\!\!\!\!\!\! \\rstharpoonup }}}&c_{5}\&#&#{\downharpoon왼쪽 }}\\\n1}&#{r:1}}&\\\\downharpoon 왼쪽 }&#&\&\&c_{2}&&r_{6}&end{matrix}}}}}}}}
다른 시스템에서 변환 본드 그래프를 사용할 때의 주요 장점 중 하나는 일단 본드 그래프를 갖게 되면 원래의 에너지 영역은 중요하지 않다는 것이다. 다음은 에너지 영역에서 본드 그래프로 변환할 때 적용되는 몇 가지 단계들이다.
전자파 전자파 문제를 본드 그래프로 해결하는 단계는 다음과 같다.
각 노드에 0정절 배치 1개의 접합부가 있는 소스, R, I, C, TR 및 GY 결합 삽입 접지(변압기 또는 집압기가 있는 경우 양쪽 모두) 전원 흐름 방향 할당 단순화 이러한 단계는 아래 예제에서 보다 명확하게 나타난다.
선형기계 선형 기계적 문제를 본드 그래프로 해결하는 단계는 다음과 같다.
각 고유 속도에 대해 1-준수를 배치하십시오(보통 질량에서). R 및 C 결합이 작용하는 1개의 결합 사이에 자체 0-준딩으로 삽입 소스 및 I 결합이 작용하는 1개의 접합부에 삽입 전원 흐름 방향 할당 단순화 이러한 단계는 아래 예제에서 보다 명확하게 나타난다.
단순화 단순화 단계는 시스템이 전자파인지 선형 기계인지에 관계없이 동일하다. 단계는 다음과 같다.
0 전원 본드 제거(접지 또는 0 속도로 인한) 결합이 3개 미만인 접합부 0개 및 1개 제거 병렬 전원 단순화 0 접합을 직렬로 결합 1개의 접합부를 직렬로 결합 이러한 단계는 아래 예제에서 보다 명확하게 나타난다.
병렬전원 병렬전력은 본드 그래프에서 전력이 병렬로 구동되는 것을 말한다. 병렬 출력의 예는 다음과 같다.
병렬전력은 0과 1준드에 대한 노력과 흐름의 관계를 상기함으로써 단순화할 수 있다. 병렬 전력을 해결하기 위해 먼저 접합부의 모든 방정식을 기록하십시오. 제공된 예를 들어, 아래 방정식을 볼 수 있다. (노력/흐름 변수가 나타내는 숫자 결합을 기록하십시오.)
f 1 = f 2 = f 3 e 2 = e 4 = e 7 e 1 = e 2 + e 3 f 2 = f 4 + f 7 e 3 = e 5 = e 6 f 7 = f 6 = f 8 f 3 = f 5 + f 6 e 7 + e 6 = e 8 {\displaystyle {\reason}f_{1}=f_{2}=f_{3}&e_{2}=e_{4}=e_{7}\e_{1}=e_{2}+e_{3} }&f_{2}=f_{4}+f_{7 }\\&\\e_{3}=e_{5}=e_{6}&f_{7}=f_{6}=f_{6}=f_{8}\f_{3}=f_{5}+f_{6}=e_{6}={5}+f_{6} }&e_{7}+e_{6 }}=e_{8}\end{nd}}}
이러한 방정식을 조작함으로써 병렬 전력을 설명하는 0과 1-준수의 등가 집합을 찾을 수 있도록 정렬할 수 있다.
예를 들어 e 3 e 6 {\ textstyle e_{3}=e_{6}, e 2 e 7 {\ textstyle e_{2}=e_{7} 1 2 e 3 {\ textstyle e_{1}=e_{2}+e_{3 }} e 1 6 e 7 {\ textstyle e_{1}=e_{6}+e_{7}} 이후 6 e e textstyle e_{6}+e_{7 }}=e_{8 이제 1 8 {\ displaystyle e_{1}=e_{8}}} . 다른 방정식을 조작하면 f 4 f 5 {\ displaystyle f_{4}=f_{5}} 필요한 관계를 결정한 후에는 병렬 전원 섹션을 새 접합부로 다시 그릴 수 있다. 예시 쇼의 결과는 아래와 같다.
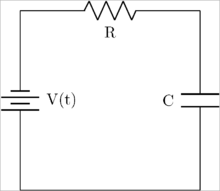
예 간단한 전기 시스템 직렬로 구성된 전압 소스, 저항기 및 캐패시터로 구성된 간단한 전기 회로.
첫 번째 단계는 모든 노드에서 0-준수를 그리는 것이다.
0 0 0 0 {\displaystyle {\displaystyle}&0&0&#\&&#&#&#&#&#&#&#&#&#&#&#&#&#&#&#&#&#&#}}}
다음 단계는 자신의 1-제곱에 따라 작용하는 모든 요소를 추가하는 것이다.
R 0 − 1 − 0 S e − 1 1 − C 0 _ − − − 0 (\displaystyle {\begin{matrix}&&&&&&&&&&&&&#&&&#&&&#&&&#&&#&#&#&#&#&#&##&##&#####&#################################### S_{e}-&&&&&&#&&&&&#\\&#&#&#&#&#&&#&#&#&#&#&#&#&#end{matrix}}}}
다음 단계는 땅을 고르는 것이다. 지면은 단순히 전압이 없다고 가정할 0접합이다. 이 경우에, 지면은 위에 밑줄 친 왼쪽 하단 0-준교로 선택될 것이다. 다음 단계는 본드 그래프의 모든 화살표를 그리는 것이다. 접합부의 화살표는 지면을 향해야 한다(전류에 유사한 경로를 따른다). 저항, 관성 및 준수 요소의 경우 화살표는 항상 요소를 향한다. 화살표 그리기의 결과는 아래를 볼 수 있으며, 0정절은 별을 지상으로 표시하였다.
이제 본드 그래프를 얻었으니 단순화 과정을 시작할 수 있다. 첫 번째 단계는 모든 접지 노드를 제거하는 것이다. 하단 0-준딩 모두 접지되어 있기 때문에 제거할 수 있다. 그 결과는 아래와 같다.
다음으로, 3개 미만의 채권을 가진 결합을 제거할 수 있다. 흐름과 노력이 이러한 접점을 수정하지 않고 통과하기 때문에 우리가 덜 그릴 수 있도록 제거될 수 있기 때문이다. 결과는 아래에서 확인할 수 있다.
마지막 단계는 본드 그래프에 인과관계를 적용하는 것이다. 인과관계 적용은 위에서 설명하였다. 최종 본드 그래프는 아래와 같다.
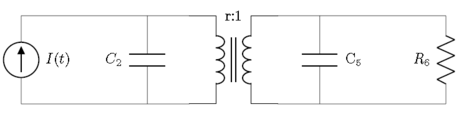
첨단 전기 시스템 전류 소스, 저항기, 캐패시터 및 변압기를 갖춘 고급 전기 시스템
이 회로의 단계를 따르면 단순화되기 전에 아래 본드 그래프가 나타난다. 별이 표시된 노드는 지면을 나타낸다.
본드 그래프를 단순화하면 아래 이미지가 생성된다.
마지막으로 인과관계를 적용하면 아래의 본드 그래프가 나타난다. 별과의 유대는 인과 갈등을 나타낸다.
단순 선형기계 벽에 부착된 스프링의 질량으로 구성된 간단한 선형 기계 시스템. 그 질량에는 약간의 힘이 작용하고 있다. 시스템 이미지는 아래와 같다.
기계적 시스템의 경우 첫 번째 단계는 각 고유 속도에 1-제곱을 배치하는 것이며, 이 경우 질량과 벽이라는 두 개의 구별되는 속도가 있다. 참조를 위해 1-준수에 라벨을 붙이는 것이 보통 도움이 된다. 결과는 다음과 같다.
1 미사 1 담을 쌓다 {\displaystyle {\cHB}&\&\&\\1_{\text{mass}&\&\&\&\&\\&\\\1_{\text{wall}&\end}}}}}
다음 단계는 R과 C 결합을 그들이 행동하는 1-준수 사이에 그들 자신의 0-준수로 그리는 것이다. 이 예에는 이러한 채권 중 봄을 위한 C 결합이 하나 있을 뿐이다. 질량을 나타내는 1절과 벽을 나타내는 1절 사이에 작용한다. 결과는 다음과 같다.
1 미사 0 − C : 1 k 1 담을 쌓다 {\displaystyle {\begin{matrix}&\&\&\\1\text{matrix}\\\text{mass}&\\\\\0&c}{\frac {1}{k}\\\\textwall}&\end{matrix}}}}}}}}}}}
다음엔 출처와 I bonds를 그들이 행동하는 1-junction에 추가하길 원한다. 노력의 원천(힘)과 I 결합의 원천인 하나의 근원이 있으며, 질량의 질량은 둘 다 질량의 1정합에 작용한다. 그 결과는 아래와 같다.
S e : F ( t ) 1 미사 − I : m 0 − C : 1 k 1 담을 쌓다 {\displaystyle {\display} S_{e}:F(t)&\\&\\\1_{\text{mass}&-I:m\\&\\\\0&C:{\frac {1}{k}\\&\\\1\\text{wall}&\end{matrix}}}}}}
다음 동력 흐름은 할당될 것이다. 전기적 예와 마찬가지로, 동력은 지면을 향해 흐르는데, 이 경우 벽의 1-정렬이 되어야 한다. 이에 대한 예외는 항상 원소를 향하는 R, C, I 본드다. 결과 본드 그래프는 아래와 같다.
이제 본드 그래프가 생성되었으니 단순화할 수 있다. 벽이 접지되어 있기 때문에(속도 0이므로), 그 교차점을 제거할 수 있다. 이와 같이 C 채권이 0-준딩되어 있으면 3개 미만의 채권을 가질 수 있기 때문에 C 채권을 제거할 수도 있다. 단순화된 본드 그래프는 아래에서 볼 수 있다.
마지막 단계는 인과관계를 적용하는 것으로, 최종 본드 그래프는 아래에서 확인할 수 있다.
고급 선형 기계 보다 진보된 선형 기계 시스템을 아래에서 볼 수 있다.
위의 예와 같이, 첫 번째 단계는 멀리 있는 각각의 속도에서 1-준수를 만드는 것이다. 이 예에서는 3개의 원거리 속도인 질량 1, 질량 2, 벽이 있다. 그런 다음 모든 본드를 연결하고 전원 흐름을 할당하십시오. 그 결합은 아래에서 볼 수 있다.
다음으로 본드 그래프를 단순화하는 과정을 시작하며, 벽의 1준경을 제거하고, 본드가 3개 미만인 접합부를 제거하는 것이다. 본드 그래프는 아래에서 볼 수 있다.
본드 그래프에는 병렬 동력이 있다. 병렬 전력 해결은 위에서 설명하였다. 그것을 해결한 결과는 아래에서 볼 수 있다.
마지막으로 인과관계를 적용하면 최종 본드 그래프를 아래에서 볼 수 있다.
상태 방정식 본드 그래프가 완성되면 시스템의 상태-공간 표현 방정식을 생성하는 데 활용할 수 있다. 국가-공간 표현은 복잡한 다차 차등 시스템을 대신 1차 방정식의 시스템으로 풀 수 있어 특히 강력하다. 국가 방정식의 일반적인 형태는
x ˙ ( t ) = A x ( t ) + B u ( t ) {\dot스타일 {\mathbf {x}}}}}}}}(t)=\mathbf {A} \mathbf {x}(t)+\mathbf {B} \mathbf {u}(t)} 여기서 x t {\textstyle \mathbf {x}(t)} 상태 변수 의 열 행렬이거나 시스템의 알 수 없는 행렬이다 x ˙ t {\textstyle {\dot {\\mathbf {x}} ) 시간 파생물 이다. u ( t {\textstyle \mathbf {u}(t)} 그리고 A {\ textstyle \mathbf {A} B {\ textstyle \mathbf {B}은( 시스템의 상태 변수는 각 C 대한 q {\textstyle q(t)} {\ textstyle p(t)} . 각 C 결합은 q t {\textstyle p(t)} t {\textstyle q(t)} .
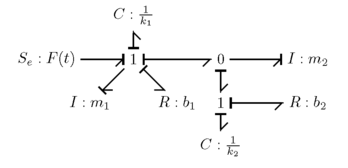
예를 들어, 다음과 같은 본드 그래프가 있는 경우
다음과 같은 ˙( t ){\textstyle dot mathbf {x (t ) {\textstyle \mathbf {x}(t) u( t {\textstyle \mathbf {u}(t)
x ˙ ( t ) = [ p ˙ 3 ( t ) q ˙ 6 ( t ) ] 그리고 x ( t ) = [ p 3 ( t ) q 6 ( t ) ] 그리고 u ( t ) = [ e 1 ( t ) ] {\displaystyle {\dot {\mathbf {x} }}(t)={\begin{bmatrix}{\dot {p}}_{3}(t)\\{\dot {q}}_{6}(t)\end{bmatrix}}\qquad {\text{and}}\qquad \mathbf {x} (t)={\begin{bmatrix}p_{3}(t)\\q_{6}(t)\end{bmatrix}}\qquad {\text{and}}\qquad \mathbf {u} (t)={\begin{bmatrix}e_{1}(t)\end{bmatrix}}}
A {\ textstyle \mathbf {A } 와) mathbf 국가 방정식을 풀기 위한 첫 번째 단계는 결합 그래프의 모든 통치 방정식을 나열하는 것이다. 아래 표는 채권과 그들의 통치 방정식의 관계를 보여준다.
"수치"는 선호되는 인과 관계를 나타낸다.
제공된 예에 대해,
지배 방정식은 다음과 같다.
입력하다 = e 1 {\textstyle {\text}=e_{1}:{1} e 1 = e 2 + e 3 + e 4 {\textstyle e_{1}=e_{2}+e_{3}+e_{4} }} f 1 = f 2 = f 3 = f 4 {\textstyle f_{1}=f_{2}=f_{3}=f_{4}}} e 2 = R 2 f 2 {\textstyle e_{2}=R_{2}f_{2}} f 3 = 1 I 3 ∫ e 3 d t = 1 I 3 p 3 {\textstyle f_{3}={\frac {1}{ I_{3}}\int e_{3}\,dt={\frac {1}{ I_{3}}p_{3}}} f 4 ⋅ r = f 5 {\textstyle f_{4}\cdot r=f_{5}} e 5 ⋅ r = e 4 {\textstyle e_{5}\cdot r=e_{4}} e 5 = e 6 = e 7 {\textstyle e_{5}=e_{6}=e_{7}} f 5 = f 6 + f 7 {\textstyle f_{5}=f_{6}+f_{7 }} e 6 = 1 C 6 ∫ f 6 d t = 1 C 6 q 6 {\textstyle e_{6}={\frac {1}{1}{{6}}}\int f_{6}\,dt={\frac {1}{1}{C_}}}}q_{6}}}}}}}{6}}}}}}}}} f 7 = 1 R 7 e 7 {\textstyle f_{7}={\frac {1}{R_{7}}e_{7}}}}{7}}}}}} 이 방정식은 국가 방정식을 산출하도록 조작될 수 있다. For this example, you are trying to find equations that relate p ˙ 3 ( t ) {\textstyle {\dot {p}}_{3}(t)} q ˙ 6 ( t ) {\textstyle {\dot {q}}_{6}(t)} p 3 ( t ) {\textstyle p_{3}(t)} q 6 ( t ) {\textstyle q_{6}(t)} e 1 ( t ) {\textstyle e_{1}(t)}
To start you should recall from the tetrahedron of state that p ˙ 3 ( t ) = e 3 ( t ) {\textstyle {\dot {p}}_{3}(t)=e_{3}(t)} e 3 = e 1 − e 2 − e 4 {\displaystyle e_{3}=e_{1}-e_{2}-e_{4}} e 2 {\displaystyle e_{2}} 방정식 4에서 f 2 {\ displaystyle f_{2}}: 인해 3 displaystyle f_{3}} e 4 {\ displaystyle e_{4} 5 e_{ 5 그런{\displaystyle e_{6}. 이러한 대체 방정식에 따라 아래 나온 첫 번째 상태 방정식이 산출된다.
p ˙ 3 ( t ) = e 3 ( t ) = e 1 ( t ) − R 2 I 3 p 3 ( t ) − r C 6 q 6 ( t ) {\dot {\p}_{3}(t)=e_{3}(t)=e_{1}(t)-{\frac{R_{2}}:{ I_{3}}}p_{3}(t)-{\frac {r}{C_{6}}q_{6}(t)}
q f 6 ( textstyle {\q 6}}(t)=f_{6}(t 두 번째 상태 방정식은 다음과 같다.
q ˙ 6 ( t ) = f 6 ( t ) = r I 3 p 3 ( t ) − 1 R 7 ⋅ C 6 q 6 ( t ) {\dot{q}_{6}(t)=f_{6}(t)={\frac {r}{{r}{ I_{3}}}p_{3}(t)-{\frac {1}{R_{7}\cdot C_{6}}q_{6}(t)}
두 방정식은 더 나아가 행렬 형태로 재배열할 수 있다. 그 결과는 다음과 같다.
[ p ˙ 3 ( t ) q ˙ 6 ( t ) ] = [ − R 2 I 3 − r C 6 r I 3 − 1 R 7 ⋅ C 6 ] [ p 3 ( t ) q 6 ( t ) ] + [ 1 0 ] [ e 1 ( t ) ] {\dot {p}_{3}(t)\\\\dot {q}{6}(t)\end{bmatrix}={\begin{bmatrix}-{\frac{R_{2}}:{\dot{q}}}}}{bematrix}-{{R_}}}}}}}}}}}}}}}}{{{{{}}}}}}}}}}}}}}}}}}}}}}} I_{3}}-{\frac {r}{C_{6}}\\\\frac {r}{{r}}{{\frac}{{r}}{{}}}}{{\frac}{r}}{ I_{3}}}&-{\frac {1}{R_{7}\cdot C_{6}}}\end{bmatrix}}{\begin{bmatrix}p_{3}(t)\\q_{6}(t)\end{bmatrix}}+{\begin{bmatrix}1\\0\end{bmatrix}}{\begin{bmatrix}e_{1}(t)\end{bmatrix}}}
이 시점에서 방정식은 다른 주-공간 표현 문제로 취급될 수 있다.
본드 그래프 모델링에 관한 국제 회의(ECMS 및 ICBGM) 본드 그래프 모델링에 대한 참고 문헌은 다음 컨퍼런스에서 추출할 수 있다.
ECMS-2013 제27회 유럽 모델링 및 시뮬레이션 컨퍼런스, 2013년 5월 27~30일 노르웨이 슐레순드 2008년 6월 3일–6일, 키프로스, 니코시아, 모델링 및 시뮬레이션에 관한 ECMS-2008 22차 유럽 회의 ICBGM-2007: 제8차 본드 그래프 모델링 및 시뮬레이션 국제회의, 2007년 1월 15-17일, 미국 캘리포니아주 샌디에이고. ECMS-2006 20 2006년 5월 28~31일 독일 본에서 열린 유럽 모델링 및 시뮬레이션 회의 IMAACA-2005 국제 지중해 모델링 멀티콘퍼런스 ICBGM-2005 Bond Graph Modeling and Simulation에 관한 국제 회의, 2005년 1월 23-27일, 미국 루이지애나 주 뉴올리언스 - 논문 ICBGM-2003 Bond Graph Modeling and Simulation (ICBGM'2003) 2003년 1월 19-23일, 올랜도, 플로리다, 미국 – 논문 제14차 유럽 시뮬레이션 심포지엄 2002년 10월 23일–26일 독일 드레스덴 2001년 10월 18일~20일 프랑스 마르세유에서 열린 ESS 제13회 유럽 시뮬레이션 심포지엄 ICBGM-2001 국제 본드 그래프 모델링 및 시뮬레이션 회의(ICBGM 2001), 미국 애리조나 주 피닉스 유럽 시뮬레이션 다중 회의 2000년 5월 23-26일 벨기에 겐트 제11회 유럽 시뮬레이션 심포지엄, 1999년 10월 26일–28일 독일 에를랑겐 뉘른베르크 프리드리히 알렉산더 대학교 캐슬 ICBGM-1999 Bond Graph Modeling and Simulation에 관한 국제 회의 1999년 1월 17~20일 캘리포니아 샌프란시스코 1997년 10월 19일–22일 독일 파사우에서 열린 제9회 유럽 시뮬레이션 심포지엄 및 전시 시뮬레이션 ICBGM-1997 제3차 본드 그래프 모델링 및 시뮬레이션 국제회의, 1997년 1월 12일-15일 애리조나 피닉스 쉐라톤-크레센트 호텔 1997년 6월 1일-4일 터키 이스탄불, 제11차 유럽 시뮬레이션 멀티콘퍼런스 ESM-1996 제10회 유럽 시뮬레이션 멀티콘퍼런스 헝가리 부다페스트, 1996년 6월 2일-6일 ICBGM-1995 Int. 본드 그래프 모델링 및 시뮬레이션 (ICBGM'95), 1995년 1월 15-18일, 네바다주 라스베이거스. 참고 항목 참조 추가 읽기 Kypuros, Javier (2013). System dynamics and control with bond graph modeling . Boca Raton: Taylor&Francis. doi :10.1201/b14676 . ISBN 978-1-4665-6075-8 Paynter, Henry M. (1960). Analysis and design of engineering systems . M.I.T. Press. ISBN 0-262-16004-8 Karnopp, Dean C.; Margolis, Donald L.; Rosenberg, Ronald C. (1990). System dynamics: a unified approach ISBN 0-471-62171-4 Thoma, Jean Ulrich (1975). Bond graphs: introduction and applications . Oxford: Pergamon Press. ISBN 0-08-018882-6 Gawthrop, Peter J.; Smith, Lorcan P. S. (1996). Metamodelling: bond graphs and dynamic systems . London: Prentice Hall. ISBN 0-13-489824-9 Brown, Forbes T. (2007). Engineering system dynamics – a unified graph-centered approach . Boca Raton: Taylor & Francis. ISBN 0-8493-9648-4 Mukherjee, Amalendu; Karmakar, Ranjit (2000). Modelling and simulation of engineering systems through bondgraphs . Boca Raton: CRC Press. ISBN 978-0-8493-0982-3 Gawthrop, P.J.; Ballance, D.J. (1999). "Chapter 2: Symbolic computation for manipulation of hierarchical bond graphs". In Munro, N. (ed.). Symbolic Methods in Control System Analysis and Design 23 -52. ISBN 0-85296-943-0 Borutzky, Wolfgang (2010). Bond Graph Methodology . London: Springer. doi :10.1007/978-1-84882-882-7 . ISBN 978-1-84882-881-0 http://www.site.uottawa.ca/~rhabash/ESSModelFluid.pdf 유체 도메인에서 본드 그래프를 모델링하는 방법 설명http://www.dartmouth.edu/~설리반/22파일/Fluid_sys_anal_w_chart.pdf 유체 도메인에서 본드 그래프 모델링 설명외부 링크 그래픽 본드 그래프 프로그래밍을 위한 Simscape Official MATLAB/Simulink 추가 라이브러리 BG V.2.1 그래픽 본드 그래프 프로그래밍을 위한 Freeware MATLAB/Simulink Add-on 라이브러리
 (가)
(가)  (는) 행렬 개체임.
(는) 행렬 개체임. (는) 벡터 객체임.
(는) 벡터 객체임. .
. 
![{\displaystyle D_{t}^{n}f(t)={\begin{cases}\displaystyle \int _{-\infty }^{t}f(t)\,dt,&n<0\\[2pt]f(t),&n=0\\[2pt]{\dfrac {\partial ^{n}f(t)}{\partial t^{n}}},&n>0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38acb65b2ed389e333bf304c89ad63d3bcaa031c)











![{\displaystyle e(t)=P\gamma \left[D_{t}^{-1}q(t)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7692277daff50e2ca1462ea8adacd3b42a4f4298)











 대한 전원은 소자가 개발한 힘이다.
대한 전원은 소자가 개발한 힘이다. 




![{\displaystyle e(t)=R\cdot \gamma \left[D_{t}^{1}q(t)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4bc60c05f94c761934ad5dd99af1196fccdff6d)









![{\displaystyle e(t)=A\cdot \gamma \left[D_{t}^{3}q(t)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/906f90a5434bfe07860ef46d61ece1330b5e80f6)


![{\displaystyle e(t)=M\cdot \gamma \left[D_{t}^{5}q(t)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50022933731458720255d7757980c239703c0ffa)















 (가) 상태 변수,
(가) 상태 변수, 







![{\displaystyle (x_{t})\ \mathrm {[m/s]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7185997670bd9fa64ca2a01b469e4abd0efd1979)

![{\displaystyle (x)\ \mathrm {[m]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e366196bbbf5135e48a8b548318806eef7b6788)






![{\displaystyle (P_{x}^{t})\ \mathrm {[N]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/58779e0a1147f7e6b932a3cbee21204f0153471b)

![{\displaystyle (P_{x}^{2t})\ \mathrm {[kg\cdot m/s]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c47689db1ec96f8ec233662eb566088daa11481)

 (는)
(는) 
 (는) 댐퍼 매개 변수임
(는) 댐퍼 매개 변수임 
 (는) 질량이다.
(는) 질량이다. 

 (가) 전기
(가) 전기 
 (는)
(는) 










 Kinetic Mobility이다.
Kinetic Mobility이다. 






















![{\displaystyle (\theta _{t})\ \mathrm {[rad/s]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e3b1772bd9962e36047458d976ff78b65481c1e)

![{\displaystyle (\theta )\ \mathrm {[rad]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c512818aeaeb28cd5f56b4e5acce62a33a0186cf)


![{\displaystyle (P_{\theta }^{t})\ \mathrm {[J/rad]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e8b7df76eb68c4e667c7b676d306c814e867ce3)

![{\displaystyle (P_{\theta }^{2t})\ \mathrm {[J\cdot s/rad]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b48d94caf479ff3f6d644060bc54fc18e683e16)

 각도 스프링 상수임
각도 스프링 상수임 








![{\displaystyle (q_{t})\ \mathrm {[A]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a4b5469d3ce77951a4e3ad46ccd107bbf5d0cff)

![{\displaystyle (q)\ \mathrm {[C]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/958f67351f5a84db2085eaa17eb8f57ab22d4800)


![{\displaystyle (P_{q}^{t})\ \mathrm {[V]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c731cfc786e6d340107769e7a47b76d6cb7b3048)

![{\displaystyle (P_{q}^{2t})\ \ \mathrm {[V\cdot s]} {\text{ or }}\mathrm {[Wb\cdot turn]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f656e21a85c6007abed6da15f518bd6a896ee996)









![{\displaystyle \gamma ^{1}\iff V=RD_{t}^{2}i\quad [H\cdot s]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f800e4f3a55d033f304da040bdf6f8d43927f6b7)










![{\displaystyle {\begin{aligned}e_{r}^{1}=M\cos(\theta )D_{t}f_{s}^{1}+f_{s}^{1}D_{t}\left[M\cos(\theta )\right]\\e_{s}^{1}=M\cos(\theta )D_{t}f_{r}^{1}+f_{r}^{1}D_{t}\left[M\cos(\theta )\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7c388a75b7327edefaa1d1fe9c60224a096d43e)















![{\displaystyle (V_{t})\ \mathrm {[m^{3}/s]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f7e0c0fde4d8a46d3c6ffa6468635cf8de49eb5)
![{\displaystyle (V)\ \mathrm {[m^{3}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/338a8c4467f8e661f1f00e3d8e742c1b97d9db53)

![{\displaystyle (P_{V}^{t})\ \mathrm {[Pa]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/41778c5e01757ce43b2d1096443ca52ea728156a)

![{\displaystyle (P_{V}^{2t})\ \mathrm {[Pa\cdot s]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/24de92580df08ee59b8f31b7ec85fd72671ccccf)











![{\textstyle A{\frac {1}{[m]^{n-1}}}\left(h+h_{0}\right)^{n-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e44dc8a514fce13c5679676c3ca6833fa72dde83)
![{\displaystyle P_{V}^{t}=\rho gh_{0}\left[\left(1+{\frac {nV}{A{\frac {1}{[m]^{n-1}}}h_{0}^{n}}}\right)^{1/n}-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e34e6a21726943ea4c2fd959d7d5cb6b38946a4)


![{\displaystyle [m]^{n-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6c478517004228cc94fca0efaa17a9af82f4dbf)



![{\displaystyle P_{V}^{t}=\rho gh_{0}\left(e^{\frac {V}{A[m]}}-1\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e7f27385447af3910d7bebc2ba9dfc561416cd1)



 경험적 모수다.
경험적 모수다. 








![{\displaystyle (\varphi )\ \mathrm {[Wb]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/76fc8df2678d11d3374eb98909bc1e4128ef79e8)

![{\displaystyle ({\mathcal {F}})\ \mathrm {[A\cdot turn]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/84407872cd52412d92122c073fc3dc44d3b63720)

![{\displaystyle \langle {\mathcal {F}}\rangle ={\frac {1}{\mu }}\phi _{L}\langle \varphi \rangle \quad \mathrm {[H/turn^{2}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d21b95cc7cec0ac9f251a3822b40e9fb62483ebc)

![{\displaystyle {\mathcal {F}}=Z_{M}{\varphi _{t}}\quad \mathrm {[{turn}^{2}/\Omega ]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9791388153b46c1158c64c60f1779460e216896)

![{\displaystyle {\mathcal {F}}=L_{M}{\varphi _{2t}}\quad \mathrm {[{turn}^{2}F]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd3edf66f8d748e530e54e2a01d9cdf6fb2c8c8c)

![{\displaystyle \left(i_{g}=2\varepsilon _{g}v_{\text{orbit}}^{3}\right)\ \mathrm {[kg/s]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4f91e27e6c19bdba9f1898ef2c593abee239400)

![{\displaystyle (M)\ \mathrm {[kg]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b34049e66306438fffaa9dd199400d5f2afbb15)

![{\displaystyle \left(V_{g}={\frac {1}{2}}{\frac {v_{\text{orbit}}^{4}}{c^{2}}}\right)\ \mathrm {[m^{2}/s^{2}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe69f40550f63b11ed90f45872588868b29ac045)

![{\displaystyle \left(\phi _{g}={\frac {\pi v_{\text{orbit}}^{3}r}{c^{2}}}\right)\ \mathrm {[m^{2}/s]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/43b3d09092d876508fe18a7f3bcfff0fa3ce8a5b)
![{\displaystyle \gamma ^{1}\iff M_{g}=CV_{g}\quad \mathrm {[kg/m^{2}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/69596aebd18b39e6de38a61affe2a43ee9208735)




![{\displaystyle (J)\ \mathrm {[A/m^{2}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/144edb9a549b5f086d6162c361b4abfe18f09135)

![{\displaystyle (D)\ \mathrm {[C/m^{2}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/32cdc82bb656447a11515b6d6cae4476d3157c7d)

![{\displaystyle (E)\ \mathrm {[V/m]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fc9227b91d0e58fc10ebac6a572450825f49e38)

![{\displaystyle (A)\ \mathrm {[V\cdot s/m]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2f011a6029ef86d0bb5c1eac467eb4144a0bb07)

![{\displaystyle \mu _{0}\ \mathrm {[H/m]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/11e81db96bdfb041df9dc7307c013640c98d7dea)

![{\displaystyle (B)\ \mathrm {[T]} {\text{ or }}\mathrm {[Wb/m^{2}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9c6904139507bfd048cfb2a80d474eb6d9818ee)

![{\displaystyle (H)\ \mathrm {[A\cdot {turn}/m]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cdd00761960594853700bd79b8c24326d426c0f)
![{\displaystyle \gamma ^{1}\iff B=\mu H\quad \mathrm {[H/(m\cdot {turn}^{2})]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8d0aec1e8f327f5ae4d00495bdb3792d05f8a20)

![{\displaystyle (J_{g})\ \mathrm {[kg/m^{2}s]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/64cd8283a05aaf84f6d5447261565be0cf8739ff)

![{\displaystyle (D_{g})\ \mathrm {[kg/m^{2}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1130b9b0e89c626b10a6bc51342c1f44da8a3e61)

![{\displaystyle (g)\ \mathrm {[m/s^{2}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac799c862aacdd37eacb2a295b02e263c46c865)



![{\displaystyle \left(B_{g}=\omega _{\text{orbit}}\left({\frac {v_{\text{orbit}}}{c}}\right)^{2}\right)\ \mathrm {[Hz]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/de9a258fa1a584b1b23ad7a67b72b4d16d802f7f)

![{\displaystyle (H_{g})\ \mathrm {[Pa\cdot s]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f2870b556cd8e28c371ccda42ce168042723af9)
![{\displaystyle -{\frac {4\pi G}{c^{2}}}\ \mathrm {[m/kg]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/172c55ce6ca52cd77e23ff42d2e9a6cb628f6511)

![{\displaystyle (\psi _{t})\ \mathrm {[W]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e0cfd1751c5576f55adf66fc0db3e155e08e641)

![{\displaystyle (\psi )\ \mathrm {[J]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/53cb7702edf24c24126d3d5f62f456d69043ad30)

![{\displaystyle (T)\ \mathrm {[K]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e7a91d9d4545d00cdd70269c0e64aa53d2dd645)




 정전용량 열 캐패시턴스임
정전용량 열 캐패시턴스임 







![{\displaystyle ({\dot {\varepsilon }})\ \mathrm {[Hz]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/943859fa977a773fcfaa8f2a4ab9ef50ec0de0fc)

![{\displaystyle (\varepsilon )\ \mathrm {[1]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2287a5fab8eae7b8cb6db4986724975870d5fded)

![{\displaystyle (\sigma )\ \mathrm {[Pa]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/784dd13d93f95d7f4014d8fe6d0b954ceb49b38e)

![{\displaystyle \rho \ \mathrm {[kg/m^{3}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e67114b96c82908eec2a7e82bf920d4b75f2dec3)
































































 관계를 설명할 수 있다. 필요한 관계를 결정한 후에는 병렬 전원 섹션을 새 접합부로 다시 그릴 수 있다. 예시 쇼의 결과는 아래와 같다.
관계를 설명할 수 있다. 필요한 관계를 결정한 후에는 병렬 전원 섹션을 새 접합부로 다시 그릴 수 있다. 예시 쇼의 결과는 아래와 같다. 








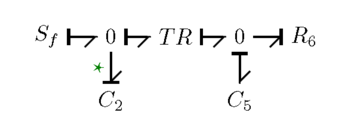














 (는) 시스템 입력의 열 행렬이다. 그리고
(는) 시스템 입력의 열 행렬이다. 그리고  (와)
(와) 

























































