중심제곱수

이 글에는 참고문헌, 관련 독서 또는 외부 링크 목록이 수록되어 있으나 인라인 인용구가 부족하여 출처가 불분명하다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오.(2016년 1월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

초등수 이론에서 중심정사각수는 중앙에 점이 있는 사각형의 점의 수와 중앙점을 둘러싼 다른 모든 점들이 연속적인 정사각형 층에서 점의 수를 나타내는 중심형 구상수다.즉, 각 중심 정사각형 숫자는 일반 정사각형 격자 위의 중심점으로부터 주어진 도시 블록 거리 내에 있는 점의 수와 같다.일반적으로 비유적 숫자와 같이 중심 정사각형 숫자는 직접적인 실용적 용도가 거의 없지만, 우아한 기하학적 특성과 산술적 특성 때문에 레크리에이션 수학에서 연구되기도 한다.

처음 네 개의 중심 정사각형 숫자에 대한 그림은 다음과 같다.

${\displaystyle C_{4,1}=1}$			${\displaystyle C_{4,2}=5}$			${\displaystyle C_{4,3}=13}$			${\displaystyle C_{4,4}=25}$

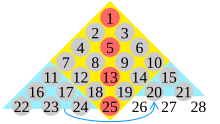
각 중심 제곱수는 연속 제곱의 합이다.예: 플로이드 삼각형의 다음 그림에서 보듯이 25는 중심 정사각형 숫자로 제곱 16(정사각형을 깎음으로써 형성된 노란색 광맥)과 다음 작은 정사각형 9(청색 삼각형 2개의 합)의 합이다.

다른 비유적 숫자와의 관계

C는_k,n 일반적으로 n번째 중심 k-곤 수를 나타낸다.n번째 중심 제곱수는 다음 공식으로 주어진다.

${\displaystyle C_{4,n}=n^{2}+(n-1)^{2}}$

즉, n번째 중심 제곱수는 n번째 제곱과 (n – 1) 제곱수의 합이다.다음 패턴은 이 공식을 나타낸다.

${\displaystyle C_{4,1}=0+1}$			${\displaystyle C_{4,2}=1+4}$			${\displaystyle C_{4,3}=4+9}$			${\displaystyle C_{4,4}=9+16}$

공식은 다음과 같이 표현할 수도 있다.

${\displaystyle C_{4,n}={\frac {(2n-1)^{2}+1}{2}.}$

즉, n번째 중심 제곱수는 아래 그림과 같이 n번째 홀수 제곱수에 1을 더한 값의 절반이다.

${\displaystyle C_{4,1}={\frac {1+1}{2}}:}$			${\displaystyle C_{4,2}={\frac {9+1}{2}}:}$			${\displaystyle C_{4,3}={\frac {25+1}{2}}:}$			${\displaystyle C_{4,4}={\frac {49+1}{2}}:}$

모든 중심 다각형 숫자와 마찬가지로 중심 정사각형 숫자도 삼각형 숫자로 표현할 수 있다.

${\displaystyle C_{4,n}=1+4\ T_{n-1}=1+2{n(n-1)},}$

어디에

${\displaystyle T_{n}={\frac {n(n+1)}{2}}}={\binom {n+1}{2}}}$

N번째 삼각형 숫자 입니다.이는 다음과 같이 중앙점을 제거하고 나머지 그림을 4개의 삼각형으로 나누면 쉽게 알 수 있다.

${\displaystyle C_{4,1}=1}$			${\displaystyle C_{4,2}=1+4\time 1}$			${\displaystyle C_{4,3}=1+4\time3}$			${\displaystyle C_{4,4}=1+4\time 6}$

연속된 두 개의 팔면수 사이의 차이는 중심 정사각형수(콘웨이와 가이, 페이지 50)이다.

중심 정사각형 수를 표현할 수 있는 또 다른 방법은 다음과 같다.

${\displaystyle C_{4,n}=1+4\dim(SO(n)),}$

어디에

${\dim(SO(n))={\frac {n(n-1)}{2}}.}$

그러나 중심 정사각형 수를 표현할 수 있는 또 다른 방법은 중심 삼각형 숫자의 측면에서 다음과 같다.

${\displaystyle C_{4,n}={\frac {4C_{3,n}-1}{3}},}$

어디에

${\displaystyle C_{3,n}=1+3{\frac {n(n-1)}{2}.}$

중심 정사각형 수 목록

첫 번째 중심 정사각형 숫자(C_4,n < 4500)는 다음과 같다.

1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, 761, 841, 925, 1013, 1105, 1201, 1301, 1405, 1513, 1625, 1741, 1861, 1985, 2113, 2245, 2381, 2521, 2665, 2813, 2965, 3121, 3281, 3445, 3613, 3785, 3961, 4141, 4325, … (sequence A001844 in the OEIS).

특성.

중심 정사각형은 모두 홀수이며, 베이스 10에서는 한 자릿수가 1-5-3-5-1 패턴을 따르고 있음을 알 수 있다.

모든 중심 정사각형 숫자와 칸막이를 4로 나누면 나머지 1이 된다.따라서 모든 중심 정사각형 숫자와 칸막이는 기본 6, 8, 12에서 숫자 1 또는 5로 끝난다.

1을 제외한 모든 중심 제곱수는 피타고라스 3중주(3-4-5, 5-12-13, 7-24-25, ...)의 하이포텐스다.가장 긴 두 변이 각각 1씩 차이가 나는 피타고라스 삼쌍의 순서(예²: 5 + 12² = 13²).

이는 관계(n– 1)2+ n2)C와4,n안 된다(예2:2+3=132)혼동해서는.

생성함수

중심 정사각형 숫자를 제공하는 생성 함수는 다음과 같다.

${\displaystyle {\frac{(x+1)^{2}}:{{{-x)^{3}}=1+5x+13x^{2}+25x^{3}+41x^{4}+...~.}$

참조

• Alfred, U. (1962), "n and n + 1 consecutive integers with equal sums of squares", Mathematics Magazine, 35 (3): 155–164, JSTOR 2688938, MR 1571197.
• Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR 0434929, Zbl 0335.10001.
• Beiler, A. H. (1964), Recreations in the Theory of Numbers, New York: Dover, p. 125.
• Conway, John H.; Guy, Richard K. (1996), The Book of Numbers, New York: Copernicus, pp. 41–42, ISBN 0-387-97993-X, MR 1411676.