참페어드 도데카헤드론
Chamfered dodecahedron| 참페어드 도데카헤드론 | |
|---|---|
 | |
| 콘웨이 표기법 | cD = t5daD = dk5aD |
| 골드버그 다면체 | GV(2,0) = {5+,3}2,0 |
| 풀레렌 | C80[1] |
| 얼굴 | 펜타곤 12개 육각형 30개 |
| 가장자리 | 120(2종) |
| 정점 | 80(2종) |
| 꼭지점 구성 | (60) 5.6.6 (20) 6.6.6 |
| 대칭군 | 이코사헤드랄 (Ih) |
| 이중 다면체 | 펜타키스 이코시다데코헤드론 |
| 특성. | 볼록한, 등변형의 |
 그물을 치다 | |
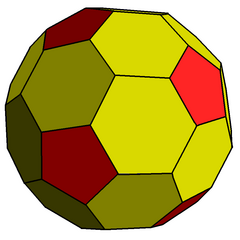
모따기 도데카헤드론은 정점 80, 가장자리 120, 면 42: 육각 30, 펜타곤 12개를 가진 볼록한 다면체다.일반 도데카헤드론의 모따기(엣지-트런케이션)로 구성된다.펜타곤은 크기가 작아지고 원래 가장자리 대신 새로운 육각면이 추가된다.그것의 이중은 펜타키스 이코시다데카헤드론이다.
그것은 또한 잘린 롬빅 3관면이라고도 불리며, 롬빅 3관면체의 잘린 형태로 만들어졌다.오더-5 정점만 잘리기 때문에 더 정확하게 오더-5 잘린 롬빅 3관면이라고 할 수 있다.
구조
이 12개의 순서-5 꼭지점은 모든 가장자리가 길이가 같도록 잘릴 수 있다.원래 30 롬빅 면은 비정규 육각형이 되고, 잘린 정점은 정규 오각형이 된다.
육각면은 등각형이 될 수 있지만 D2 대칭으로 정규적이지는 않다.꼭지점 구성 6.6.6이 있는 두 꼭지점의 각도는 아크코(-1/sqrt(5) = 116.565°이며, 나머지 4 꼭지점에서는 5.6.6이 각각 121.717°이다.
골드버그 다면체 GV(2,0)로, 오각형과 육각형의 얼굴을 포함하고 있다.
또한 6개 중 하나인 120셀(콘벡스 정규 4폴리토페스)의 세포 중심 직교 투영법 외피도 나타낸다.
화학
이것은 풀러렌 C의80 형상이다; 때때로 이 모양은 그것의 고두 대칭을 묘사하고 그것을 다른 덜 대칭적인 80-Vertex 풀러렌들과 구별하기 위해 C80(Ih)로 표시된다.Deza, Deza & Grishukhin (1998) CITREFDezaDeza (에 의해1 발견된 단 4개의 풀레네 중 하나이다.
관련 다면체
이 다면체는 12개의 펜타곤이 있지만 20개의 육면체만 있는 균일한 잘린 이코사면과 매우 닮았다.
잘린 이코사면체
G(1,1)
모따기 도데카헤드론은 기본 콘웨이 다면체 표기법에 의해 더 많은 다면체를 만든다.지퍼 모따기 도데카헤드론은 모따기 잘린 이코사헤드론과 골드버그(22)를 만든다.
| "seed" | 암보 | 잘게 자르다 | 지퍼를 채우다 | 확대하다 | 베벨을 울리다 | 코를 납작하게 만들다 | 모따기 | 빙글빙글 돌다 |
|---|---|---|---|---|---|---|---|---|
 cD = G(2,0) cd |  ACD ACD |  tcD tcD |  zcD = G(2,2) zcD |  ecD ecD |  BCD BCD |  scd scd |  ccD = G(4,0) ccD |  wcD = G(4,2) wcD |
| 이중의 | 합류하다 | 바늘을 꿰다 | 키스하다 | 정형외과 | 내면의 | 자이로 | 듀얼 챔퍼 | 이중 회전 |
 dcd dcd |  jcd jcd |  ncD ncD |  kcd kcd |  강박증 강박증 |  mcd mcd |  gcD gcD |  dccD dccD |  dwcD dwcD |
챔페어드 잘린 이코사면체
| 챔페어드 잘린 이코사면체 | |
|---|---|
 | |
| 골드버그 다면체 | GV(2,2) = {5+,3}2,2 |
| 콘웨이 표기법 | CTI |
| 풀레렌 | C240 |
| 얼굴 | 펜타곤 12개 110 육각형(3종) |
| 가장자리 | 360 |
| 정점 | 240 |
| 대칭 | Ih, [5,3], (*532) |
| 이중 다면체 | 헥사펜타키스 챔페이드 도데카헤드론 |
| 특성. | 볼록하게 하다 |
기하학에서 모따기 잘린 이코사헤드론은 정점 240, 가장자리 360, 면 122, 육각 110, 펜타곤 12개를 가진 볼록한 다면체다.
잘린 이코사면에 모따기 연산에 의해 구성되며, 원래의 가장자리 대신 새로운 육각형을 추가한다.모따기 도데카헤드론에서 지퍼(=dk = kis의 이중) 조작으로도 제작할 수 있다.즉, 모따기 도데카헤드론(kis 연산)에 오각형 및 육각형 피라미드를 올리면 (2,2) 지오데믹 다면체를 산출하게 된다.그 이중으로 보면 (2,2)골드버그 다면체(Goldberg)를 산출하는데, 이 다면체(Chamfered cuted icosaheadron)는 모가 잘린 이코사면체(chamfered called icosheadron)이며240, 풀레렌 C
이중
그것의 이중인 헥사펜타키스 챔페이드 도데카헤드론은 240개의 삼각면(파란색으로 그룹화), 약 12개의 5배 대칭 정점 12개와 약 120개의 6배 대칭 정점 20개, 360개의 가장자리 및 122개의 정점을 가지고 있다.
참조
- ^ "C80 Isomers". Archived from the original on 2014-08-12. Retrieved 2014-08-05.
- Goldberg, Michael (1937). "A class of multi-symmetric polyhedra". Tohoku Mathematical Journal. 43: 104–108.
- Hart, George (2012). "Goldberg Polyhedra". In Senechal, Marjorie (ed.). Shaping Space (2nd ed.). Springer. pp. 125–138. doi:10.1007/978-0-387-92714-5_9. ISBN 978-0-387-92713-8.
- Hart, George (June 18, 2013). "Mathematical Impressions: Goldberg Polyhedra". Simons Science News.
외부 링크
- 정점 변환 폴리헤드라 리비오 제피로로 이어지는 플라토닉 및 아르키메데스 고형물의 정점 및 가장자리-트랜지션
- VRML 다면 발생기(콘웨이 다면 표기법)







