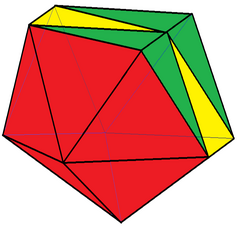
가장자리-계약 이코사면체
Edge-contracted icosahedron| 가장자리-계약 이코사면체 | |
|---|---|
 | |
| 얼굴 | 삼각형 18개 |
| 가장자리 | 27 |
| 정점 | 11 |
| 대칭 | C2v, [2], (*22), 주문 4 |
| 꼭지점 구성 | 2 (34) 8 (35) 1 (36) |
| 특성. | 볼록, 삼각면 |
| 그물 |  |
기하학에서 가장자리 수축형 이코사헤드론은 삼각형 면 18개, 가장자리 27개, 정점2v 11개, 순서 4를 갖는 다면체다.
건설
그것은 하나의 가장자리 수축, 하나의 꼭지점, 3개의 가장자리, 그리고 2개의 면을 제거하는 일반적인 이코사면으로부터 건설될 수 있다.이 수축은 한정된 구체의 원래 정점을 왜곡한다.모든 정삼각형 면에 3개의 정삼각형(각각 반헥사곤을 형성함)이 2세트 들어 있어 존슨 고체가 아니다.
3개의 동일 평면 삼각형 세트를 하나의 면(삼각형이라고[1] 함)으로 본다면 정점 10개와 가장자리 22개, 그리고 14개의 면, 12개의 삼각형, 2개의 삼각형 2개가 있다.
또한 하이브리드 사각형-펜타곤 항정신병 코어(한 칸 베이스와 오각형 베이스가 각각 하나씩 있는 항정신병 코어)를 갖는 것으로 설명할 수 있다. 그런 다음 각 베이스는 피라미드로 증강된다.
관련 폴리토페스
해부된 일반 이코사헤드론은 세 개의 코플란라 면의 두 세트가 사다리꼴로 되어 있는 스테노코로나와 지형학적으로 동등한 변종이다.이것은 4D 폴리토페, 대항정신병(Grand Antiratism)의 꼭지점이다.정점 10개, 가장자리 22개, 삼각형 12개, 사다리꼴 2개 등이다.[2]
화학에서
화학에서, 이 다면체는 가장 흔히 18개의 삼각형 면에 대해 팔면체라고 불리며, 클로토-보라네이트[BH1111]2−를 나타낸다.[3]
-dianion-from-xtal-3D-bs-17.png) 볼앤스틱 모델 쇄석-결핵 이온, [BH1111]2− |  밀폐[BH1111]2− |  그물 |
관련 다면체
길쭉한 팔면체는 가장자리가 수축된 이코사면체와 유사하지만 한쪽 가장자리만 수축되는 대신 반대쪽 가장자리 두 개가 수축된다.
참조
- ^ "Convex Triamond Regular Polyhedra".
- ^ 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, 2008년 사물의 대칭성, ISBN 978-1-56881-220-5 (제26장) 대척성
- ^ Holleman, Arnold Frederik; Wiberg, Egon (2001), Wiberg, Nils (ed.), Inorganic Chemistry, translated by Eagleson, Mary; Brewer, William, San Diego/Berlin: Academic Press/De Gruyter, p. 1165, ISBN 0-12-352651-5
