명명된 그래프 갤러리

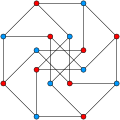
그래프 이론에서 고려된 유한 구조들 중 일부는 이름이 있으며, 때로는 그래프의 위상에서 영감을 얻기도 하고, 때로는 발견자의 이름을 찾기도 한다.유명한 예로는 피터슨 그래프가 있는데, 10개의 꼭지점에 있는 콘크리트 그래프로서, 이 그래프는 여러 가지 다른 맥락에서 최소의 예로 나타나거나 또는 counterexample로 나타난다.

개별 그래프

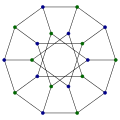
대칭성이 높은 그래프

매우 정규 그래프

v 꼭지점과 순위 k에 대한 강한 정규 그래프는 보통 srg(v,k,,,μ)로 표시된다.

대칭 그래프

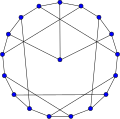
대칭 그래프는 대칭(그래프 자동모형)이 정렬된 다른 쌍의 인접 정점 쌍을 다른 쌍으로 가져가는 대칭이다. 포스터 인구조사에서 모든 작은 대칭 3-정규 그래프를 나열한다.모든 강력한 정규 그래프는 대칭이지만, 그 반대는 아니다.

반대칭 그래프

그래프 패밀리

전체 그래프

$n$ $n$ 정점에 $n$ 대한 전체 그래프는 $종종$ n{\ $displaystyle$ n} -clike라고 $n$ 불리며, 보통 독일 콤플렛에서 $K_{n}$ ${\$ 을 가리킨다.^[1]

${\displaystyle K_{1}.$
$K_{2}$
$K_{3}$
$K_{4}$
$K_{5}$
$K_{6}$
$K_{7}$
$K_{8}$

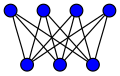
완전한 초당적 그래프

완전한 초당적 그래프는 일반적으로 $K_{n,m}$ $K_{n,m}$ , $K_{n,m}$ ${\$ 로 표시된다 $K_{n,m}$ $n=1$ = $n=1$ ${\displaystyle n=1$ }은 $n=1$ $($ 는) 별 그래프 섹션을 참조하십시오.그래프 $K_{2,2}$ $K_{2,2}$ , $K_{2,2}$ ${\$ 은 아래에 소개된 4 $C_{4}$ $C_{4}$ 4 ${\$ 사각형)와 같다 $K_{2,2}$ .

$K_{2,3}$
$K_{3,3}$ $K_{3,3}$ , $K_{3,3}$ 3 ${\$ 유틸리티 그래프
$K_{2,4$
$K_{3,4$

사이클

$n$ $n$ 정점에 $n$ 대한 사이클 그래프를 n 사이클이라고 하며, 보통 $C_{n}$ $C_{n}$ ${\$ 을 나타내며 $C_{n}$ 주기 그래프, 다각형 또는 n-곤이라고도 한다.특별한 경우는 삼각형 $C_{3}$ ${\$ $C_{4}$ C $C_{4}$ {\ $displaystyle C_{4$ 그리고 그리스어 이름인 펜타곤 C $C_{5}$ ${\$ $C_{6}$ $C_{6}$ 6 ${\$ 등이 있다 $C_{6}$

$C_{3}$
$C_{4}$
$C_{5}$
$C_{6}$

우정 그래프

우정 그래프 F는_n 주기 그래프 C의₃ n개의 복사본을 공통 꼭지점과 결합하여 구성할 수 있다.^[2]

우정 그래프는₂ F, F₃, F₄.

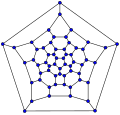
풀레렌 그래프

그래프 이론에서 풀레렌이라는 용어는 모든 얼굴이 5 또는 6(외면 포함) 크기의 3-정규 평면 그래프를 의미한다.오일러의 다면체 공식인 V – E + F = 2(여기서 V, E, F는 정점, 가장자리 및 면의 수를 나타냄)에서 따르며 풀러렌에는 정확히 12개의 펜타곤과 h = V/2 – 10개의 육각형이 있다.따라서 V = 20 + 2h, E = 30 + 3h.풀레렌 그래프는 해당 풀레렌 화합물의 슐레겔 표현이다.

20-풀레렌(도데카헤드 그래프)
24-풀레렌(헥사사각형 잘린 사다리꼴 그래프)
26-풀레렌 그래프
60-풀레렌(축소된 이두면 그래프)
70풀레렌

주어진 수의 육각면으로 모든 비이형 풀렌을 생성하는 알고리즘은 G. 브링크만과 A에 의해 개발되었다.드레스.^[3] G. 브링크만은 또한 풀젠이라 불리는 자유롭게 이용할 수 있는 구현을 제공했다.

플라톤 고형

4개의 정점에 있는 완전한 그래프는 4면체의 골격을 형성하며, 더 일반적으로 완전한 그래프는 단순함의 골격을 형성한다.하이퍼큐브 그래프는 또한 고차원 일반 폴리토페스의 골격이기도 하다.

큐브
$n=8$ = $n=8$ ${\displaystyle n=8$ $m=12$ = $m=12$ $m=12$
팔면체
$n=6$ = $n=6$ ${\displaystyle n=6$ $m=12$ = $m=12$ $m=12$
도데카헤드론
$n=20$ = $n=20$ ${\displaystyle n=20$ $m=30$ = $m=30$ $m=30$
이코사헤드론
$n=12$ = $n=12$ ${\displaystyle n=12$ $m=30$ = $m=30$ $m=30$

잘린 고체

스나크스

스나크는 브리지가 없는 입방 그래프로, 적절한 가장자리 색상에 4가지 색상이 필요하다.가장 작은 스나크는 피터슨 그래프인데, 이미 위에 나열되어 있다.

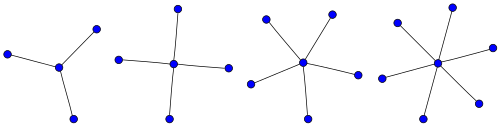
별

별 S는_k 완전한 초당적 그래프 K이다_1,k.별 S는₃ 집게 그래프라고 불린다.

별은 S₃, S₄, S₅, S를₆ 그래프로 표시한다.

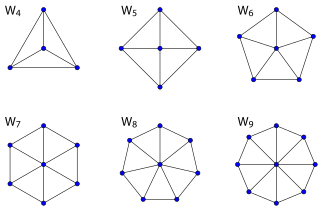
휠 그래프

휠 그래프 W는_n (n - 1) 사이클의 모든 꼭지점에 단일 꼭지점을 연결함으로써 구성된 n 꼭지점에 대한 그래프다.

휠

W_{4}

W_{4}

{\

W_{4}

–

W_{9}

W_{9}

{\

참조

^ 데이비드 그리스와 프레드 B.Schneider, 이산수학에 대한 논리적 접근, Springer, 1993, p 436.
^ 갈리안, J. A. "동적 조사 DS6: 그래프 라벨링"Electronic Journal of Combinatorics, DS6, 1-58, 2007년 1월 3일.[1] 웨이백머신에 보관된 2012-01-31.
^ Brinkmann, Gunnar; Dress, Andreas W.M (1997). "A Constructive Enumeration of Fullerenes". Journal of Algorithms. 23 (2): 345–358. doi:10.1006/jagm.1996.0806. MR 1441972.

[1] 데이비드 그리스와 프레드 B.Schneider, 이산수학에 대한 논리적 접근, Springer, 1993, p 436.

[2] 갈리안, J. A. "동적 조사 DS6: 그래프 라벨링"Electronic Journal of Combinatorics, DS6, 1-58, 2007년 1월 3일.[1] 웨이백머신에 보관된 2012-01-31.

[3] Brinkmann, Gunnar; Dress, Andreas W.M (1997). "A Constructive Enumeration of Fullerenes". Journal of Algorithms. 23 (2): 345–358. doi:10.1006/jagm.1996.0806. MR 1441972.

[1]

[2]

[3]

Search