기하학 대수
Geometric algebra수학에서, 기하학 대수(실제 클리포드 대수라고도 함)는 벡터와 같은 기하학적 물체를 다루기 위한 기초 대수학의 확장이다.기하학적 대수는 덧셈과 기하학적 곱이라는 두 가지 기본 연산으로 구성됩니다.벡터의 곱셈은 다차원이라고 불리는 더 높은 차원의 객체를 낳는다.기하학적 객체를 조작하기 위한 다른 형식과 비교하여, 기하학적 대수는 다른 차원의 객체의 벡터 분할 및 추가를 지원하는 데 주목할 만하다.
기하학적 곱은 헤르만 그라스만에 의해 처음 간략하게 언급되었는데, 헤르만 그라스만은 [1]밀접하게 연관된 외부 대수학을 개발하는 데 주로 관심이 있었다.1878년, 윌리엄 킹던 클리포드는 그라스만의 연구를 크게 확장하여 클리포드 대수를 형성하였다. (클리포드 자신은 그것들을 "기하 대수"라고 부르기로 선택했지만).클리포드는 클리포드 대수와 그 곱을 그래스만 대수와 해밀턴 사분위 대수의 통합으로 정의했다.그라스만 외부 곱의 쌍대수("meet")를 더하면 그라스만-케일리 대수를 사용할 수 있고, 등각 클리포드 대수와 함께 후자의 등각 버전은 고전 [2]기하학을 위한 프레임워크를 제공하는 등각 기하학 대수를 산출한다.실제로, 이것들과 몇 가지 파생 연산을 통해 대수의 요소, 부분 공간 및 연산을 기하학적 해석과 일치시킬 수 있다.수십 년 동안 기하학 대수는 어느 정도 무시되었고, 그 후 전자기학을 설명하기 위해 새롭게 개발된 벡터 미적분에 의해 크게 가려졌다."기하 대수"라는 용어는 상대론적 물리학의 중요성을 [3]주창했던 헤스테네스에 의해 1960년대에 다시 대중화 되었다.
스칼라와 벡터는 통상적인 해석을 가지며 기하학적 대수의 뚜렷한 부분 공간을 구성한다.바이벡터는 벡터 대수에서 방향 영역, 방향 회전각, 토크, 각운동량 및 전자장과 같은 의사벡터 양을 보다 자연스럽게 표현합니다.트라이벡터는 지향적인 볼륨을 나타낼 수 있습니다.라고 하는 요소를 사용하여 공간 및 해당 부분 공간에 대한 직교 투영을 나타낼 수 있습니다.회전과 반사는 요소로 표시됩니다.벡터 대수와 달리, 기하학 대수는 자연스럽게 상대성 이론과 같은 모든 2차 형식과 차원을 수용합니다.
물리학에서 적용되는 기하학적 대수의 예로는 시공간 대수(및 물리공간의 덜 일반적인 대수)와 등각 기하학 대수(conformal 기하학 대수)가 있다.미분과 적분을 통합한 GA의 확장인 기하학 미적분은 예를 들어 미분 형식 대신 클리포드 대수를 사용함으로써 복소 해석과 미분 기하학과 같은 다른 이론을 공식화하는 데 사용될 수 있다.기하학 대수학은 데이비드 헤스틴스와[4] 크리스 [5]도란이 물리학을 위해 선호하는 수학적 틀로서 주장되어 왔다.지지자들은 이것이 고전과 양자역학, 전자기 이론과 상대성 [6]이론을 포함한 많은 분야에서 콤팩트하고 직관적인 설명을 제공한다고 주장한다.GA는 또한 컴퓨터[7] 그래픽과 로봇 공학에서 계산 도구로 사용되었습니다.
정의 및 표기법
기하학적 대수를 정의하는 방법에는 여러 가지가 있다.헤스테네스의 원래 접근법은 [8]자명하고, "기하학적 중요성으로 가득 차 있으며" 보편적 클리포드 [9]대수와 동등했다.대칭 쌍선형 형태(예: 유클리드 또는 로렌츠식 메트릭)의 F F 위에 유한 차원 2차 V {\ V가 주어진 경우 g: × {\ g VF 이 2차 공간의 기하학적 대수는 클리포드 Clδ ( ) {{이다. 이 문서의 나머지 부분에서는, 이 영역의 통상대로, {\ F=\ 만으로 간주될 것이다G(p ,) { style \{ (, ,) { { G } ( p , , r ) { g( , , )} ( , 、 q ){ , () 입니다.
대수학에서 필수적인 곱은 기하학적 곱이라고 불리며, 포함된 외부 대수의 곱은 외부 곱이라고[a] 불린다.이들을 각각 병치(즉, 명시적 곱셈 기호 생략)와 기호{\(\로 나타내는 것이 표준이다. 위의 기하학적 대수의 정의는 추상적이므로 다음과 같은 일련의 공리로 기하학적 곱의 특성을 요약한다.기하학적 곱은 A G ( ,) { A , , \ \ { G }p , } has has has hasties 。
- BG ( ,) { AB { \ {} ( , ) } (폐쇄)
- A {\ 서1 {\ 1은 ID 요소(ID 요소)입니다.
- C ) (B {\(BC)=( (관련성)
- 및 (+ ) + A {\배급)
- 2 ( , ) {\ a}= 서\a는 대수의 부분 V {\ V의 요소이다.
위의 마지막 속성이 above \a \ V a= 0 \ a 으로 대체되는 것을 제외하고 외부 제품의 특성은 동일합니다.
위의 마지막 속성에서는 gg가 양의 정의가 아닌 실수 a g가 음이 아닐 필요가 있습니다.기하학적 곱의 중요한 특성은 곱셈 역수를 가진 원소의 존재이다.a(\ a의 경우 2 0 a 0의 a (\a이 하며 g a - 과 .\g(1}a}a와 같습니다.대수의 비제로 요소는 반드시 역승수를 가질 필요는 없습니다.예를 들어,({u})가V V의 벡터이며, (\}인 경우, 1는 중요하지 않은 소수점 요소이며 [b]0이 아닙니다.
으로 R (p , ) \) V G ( ) 、 ( , q ) → G ( p , q ) ) 。스칼라 및 벡터라는 용어는 각각 R{\V {\ V의 요소(및 이 삽입에 따른 이미지)를 나타냅니다.
기하학적 곱
a(\ a와 b b의 경우 대칭곱과 반대칭곱의 합으로 aa)와(\displaystyle b의 기하학적 곱을 쓸 수 있습니다.
따라서 우리는 벡터의 내적을[c] 다음과 같이 정의할 수 있다.
그래서 대칭곱은 다음과 같이 쓸 수 있다.
는 완전히 대수에 의해 결정된다반대칭 부분은 포함된 외부 대수의 곱인 두 벡터의 외부 곱이다.
그 후 간단한 추가:
- b + b { abb+ b 기하학적 곱의 일반화되지 않은 형태 또는 벡터 형태.
내부 및 외부 곱은 표준 벡터 대수의 익숙한 개념과 연관되어 있습니다.기하학적으로 기하학적 곱이 내부 곱과 같다면와하고 와외부 곱과 같다면 수직입니다.0이 아닌 벡터의 제곱이 양수인 기하대수에서 두 벡터의 내적을 표준 벡터 대수의 도트곱과 동정할 수 있다.두 벡터의 외부 곱은 부호가 있는 면적이 벡터인 평행사변형으로 둘러싸인 것으로 식별할 수 있다.의 벡터(양정 2차 형식의 교차곱은 외부곱과 밀접하게 관련되어 있습니다.
관심있는 기하학적 대수의 대부분의 예들은 2차 형식이 비퇴출적이다.만약 2차 형식이 완전히 퇴화된다면, 어떤 두 벡터의 내부곱은 항상 0이 되고, 기하대수는 단순히 외부대수가 된다.달리 명시되지 않은 한, 이 논문은 비배출 기하학적 대수만을 다룰 것이다.
외부 곱은 자연스럽게 대수의 두 요소 사이의 연관 쌍선형 2진 연산자로 확장되어 동일성을 충족한다.
여기서 합계는 지수의 모든 순열 위에 있으며, () \은 순열의 기호이며 \는 벡터(대수의 일반 요소가 아님)이다.대수의 모든 원소는 이 형식의 곱의 합으로 표현될 수 있기 때문에, 이것은 대수의 모든 원소의 쌍에 대한 외부 곱을 정의한다.이는 외부곱이 교대대수를 형성한다는 정의에서 비롯된다.
블레이드, 그레이드 및 표준 베이스
.[e]학년 r{r\displaystyle}의 날개의 합인 Amultivector학년 r{r\displaystyle}의(균질)multivector라고 불린다 r의 외부 제품{r\displaystyle}일차 독립 벡터 Amultivector 칼날급은 r의 것으로 알려져 있{r\displaystyle}. 공리부터라고 불린다.,wih 폐색, 기하학적 대수의 모든 멀티벡터는 블레이드의 합이다.
r r}의 독립벡터 { 세트를 벡터 공간의 r r차원 서브스페이스에 고려합니다.이를 통해 실제 대칭 행렬을 정의할 수 있습니다(그라미 행렬과 같은 방식으로).
정리에 따르면 O\{O에 의해A(\ {A를 대각행렬 (\\ {D로 대각화할 수 있다.
직교 기저 벡터라고 하는 새로운벡터 { 1, , r { \ {_ {1} , \,_ {} 를 정의합니다.
직교 변환은 내부 생성물을 보존하므로, e [ ] i {\이므로{ , {는 수직이 됩니다.즉, 두 개의 서로 다른 e j\ \ 의 기하학적 곱은 외부 곱에 의해 완전히 지정됩니다.
rr의 모든 는 r r벡터의 곱으로 쓸 수 있습니다.보다 일반적으로 축퇴 기하학 대수가 허용되면 직교 행렬은 비축퇴 블록에서 직교하는 블록 행렬로 대체되고 대각 행렬은 축퇴 치수를 따라 제로 값 엔트리를 가진다.비발생 부분공간의 새로운 벡터가 다음과 같이 정규화되면
그런 다음 정규화된 벡터는 + 또는로제곱해야 합니다. 실베스터의 관성의 법칙에 따라 + +1의 총 대각 을 따른 -1의총 수는 변하지 않습니다.확장으로+의제곱인 벡터 p의 p+1)와의 제곱인 (\q)는 불변합니다.(0의 제곱인 베이시스 벡터의 합계수도 불변하며, 퇴화 대소문자가 0일 경우 0이 아닐 수 있습니다.허용됩니다.)우리는 이 G ( ,q) ( \ \} ( , )。예를 들어 G( ,0 )는 3차원 유클리드 (,) \ \ { G ( , 3 ) 、 time ( ) 。3차원 공간의 공식 기하 대수
빈 곱으로 1{\ 1을 한 지수를 오름차순으로 갖는 n{\ n개의 직교 기저 벡터의 한 모든 곱의 집합은 전체 기하학적 대수(PBW 정리 유사)의 기초를 형성한다.예를 들어 기하학적 G(3 의 는 다음과 같습니다.\
이와 같이 형성된 기저를 기하학적 대수의 표준기초라고 하며 의 다른 직교기초(\ V는 또 다른 표준기초를 생성합니다.각 표준 베이스는 2 요소로 됩니다.기하대수의 모든 멀티벡터는 표준기초요소의 선형결합으로 표현될 수 있다.표준 기본 요소가{ i i S}({i}\ i S이고 SS})가 인덱스 세트인 경우 두 멀티벡터의 기하학적 곱은 다음과 같습니다.
" k -벡터라는 용어는 한 등급의 요소만을 포함하는 멀티벡터를 설명하기 위해 자주 사용됩니다.고차원 공간에서는 이러한 멀티벡터 중 일부는 블레이드가 아닙니다(k k\ k 벡터의 곱에 포함할 수 없습니다).를 들어 + { ( 4,)의}\ 4} { {G4)}은 인수분해할 수 없지만 일반적으로 이러한 대수의 요소는 회전 등의 기하학적 양을 나타낼 수 있지만 객체로서의 기하학적 해석에 굴복하지 않는다 ({ 0, ( 및 n} -벡터만 항상 n n -스페이스 내에서 가 됩니다.
등급 투영
직교 베이스를 이용하여 등급화된 벡터 공간 구조를 확립할 수 있다.1displaystyle 의 스칼라 배수인 기하학적 대수의 요소는 0 0 이며 스칼라라고 합니다. 1, n 범위에 있는 멀티벡터는 블레이드이며 일반 벡터입니다. j 1i < n { \ { e } e_ {} \ 1 \i < j \ n\ }의 범위에 포함되는 멀티벡터는 블레이드로 바이벡터입니다.이 용어는 마지막 인n개의 n개의 벡터까지 계속됩니다.또는 { n } 블레이드를 pseudoscalar, grade-( -){ ( )블레이드 의사 디바이스 등이라고 부릅니다.대수의 많은 요소들은 다른 등급의 요소들의 합이기 때문에 이 체계에 의해 등급이 매겨지지 않는다.그러한 요소들은 혼합 등급이라고 알려져 있다.다중 벡터의 등급 매김은 원래 선택한 기준과 독립적입니다.
이것은 벡터 공간으로서의 채점이지만 대수학으로서의 채점은 아닙니다. r 블레이드 및 s s 의 곱은 0 0 ~ r 블레이드 범위에 되므로 기하학적 대수는 필터링된 대수입니다.
A(\ A는 등급 투영 연산자A A로 분해할 수 있으며, 이 연산자는 A A의 등급(\ r 부분을 출력합니다. 그 결과:
를 들어, = a + adisplay b a b 0 +a 2 { = a \ + a \ display b b = \ \ _ { 0} + \ rangle_ {2 b= b b displayle b display 0 display 0 . 。0 2의의 adisplaystyle i \ \ 。
의 분해는 짝수 홀수 컴포넌트로 나눌 수도 있습니다.
는 Z\ - 그레이드 벡터 공간에서 Z \ - 그레이드 벡터 공간으로 구조를 결과입니다.기하학적 곱은 이 거친 등급 설정을 존중합니다.따라서 기하학적 대수는 등급 벡터 공간일 뿐만 (\{2}) 등급 대수 또는 슈퍼 대수도 됩니다.
짝수로 제한하면, 두 개의 짝수 원소의 곱도 짝수이다.즉, 짝수 멀티벡터가 짝수 서브대칭을 정의합니다.n 차원 기하 대수의 짝수 하위 대수는 (여과 또는 정지 상태를 유지하지 않고) (- ( 차원의 완전한 기하 대수에 동형입니다.를 들어 + ( 2, ) ( 0, + ( 2 )\ { { ( , 1 ) G+ ( , ) G( 3 , 0 + + } ( 1 , 3 ) { } { \ G } { 3 } { 3 { 3} { 3 \ } { 3 } { 3 }
서브스페이스의 표현
기하학적 대수는 블레이드로서 V V의 부분공간을 나타내므로 V V로부터의 와 같은 대수로 공존합니다.VV의 차원 W W는 직교 { …로 표현됩니다. 1}, 및 기하학적 곱을 사용하여 D 1 2 k D1}를 형성합니다.W W를 블레이드가 여러 개 있습니다. W W를 블레이드는 모두DD의 스칼라 배수입니다.이러한 블레이드는 D(\ D)의 의 배수및 D(\)의 음의 양의 배수입니다.의은D와 같고 음의 방향은 반대 방향의 배라고 합니다.
투영, 회전 및 반사와 같은 기하학적 연산은 n(된 등급 n(n) - 블레이드가 제공하는 외부 을 통한 인수율에 의존하지만( 등급 n(표시 스타일 n - 4( 스타일 n)의 멀티플렉터가 제공하지 않기 때문에 n 스타일 n) - 。
단위 의사값
유닛 의사 스칼라는 GA에서 중요한 역할을 하는 블레이드입니다.V V의 비퇴화 부분 W(\ W에 대한 단위 의사 단위 W(\displaystyle W)는W(\W에 대한 직교 정규 기반 부재의 산물입니다. I I와 I I가 단위임을 수 있습니다. W 다음 I ± \ I=\I' I ± { I}=\1에 직교 정규 기저를 선택하지 않으면 플뤼커는 외부 대수에 벡터를 포함하지만 스케일업만 제공합니다.기하학적 대수와 외부 대수 사이의 벡터 공간 동형성을 사용하면 α에 대해 I \의등가 클래스를 얻을 수 있습니다.직교 정규성은 위의 부호를 제외하고 이 애매함을 없앱니다.
n\ \ { { } ^ { n } 위의 양의 유한 내적을 갖는 기하학적 G ( ,) { { } ( , )가 형성되었다고 가정합니다. n {^{n의 평면(2차원 부분 공간)이 주어지면 평면에 걸친 직교 정규 기저 , b 1}, 를 찾을 수 있으므로 단위 b 2를 구할 수 있다. 1 2({의 에 있는 두 벡터의 기하학적 곱은 { + I R _에 있습니다. _ 즉 0 와 2(\2) -벡터의 합계입니다.
기하학적 곱의 성질에 b 2 - -{ I} } b_{2} - 1}} 2} 가상 단위와 유사성은 부수적이지 않습니다. 부분공간 { + I i R { _ _} _ 는복소수와동형이다.이와 같이 복소수 복사는 2차 형식이 확실한 2차원 부분공간에 대한 기하학적 대수에 포함된다.
물리방정식에서 가상단위의 존재를 식별할 수 있는 경우가 있습니다.이러한 단위는 에 제곱하는 실수 대수의 많은 양 중 하나에서 발생하며, 대수의 특성과 다양한 부분 공간의 상호작용 때문에 기하학적 의미를 갖는다.
( 3, ){ {{ (0} 에서는, 한층 더 친숙한 케이스가 발생합니다.V{\ V의 직교 정규 로 구성된 표준 베이스가 주어진 경우, 의모든 \2개의 벡터 세트는 다음과 같이 확장됩니다.
으로 대문자 표기법에서 벗어남)에 라벨을 붙이면 00 및 2(\ 2) 로 생성되는 서브스페이스는 { + + j 2 + ∈ dis dis R ( ) { style)입니다. __{1_{_{ _ 이 세트는 G3의 짝수 서브대수로 간주됩니다.\{\ {G은 다음과 같습니다
이중 베이스
1, { \ { e { , \, e { } } aV { V}의 기초가 됩니다.즉 n { n - 차원 벡터 V { V에 있는 n{\displaystyle n의 독립 벡터 세트입니다.{ 1, { \ { e { , \, { } } { 、 \ { * } of of of 、 { e 1,…, ^ { } \ 。입력
서 은 크로네커 델타입니다.
V{\ V의 비퇴출 2차 형식이 주어지면 V{\ V는 자연스럽게V {\ V와 동일하며 이중 베이스는 V{\ V의 로 간주될 수 있지만 일반적으로 원본 베이스와 동일하지는 않습니다.
V V의 GA가 더 주어지면
pseudoscalar( ±11의 제곱은 아닙니다)는 {1, }(\의기본에서 형성됩니다.이중 기저 벡터는 다음과 같이 구성될 수 있다.
여기서 e {e는 i i의 기본 벡터가 제품에서 누락되었음을 나타냅니다.
내외장 제품 확장
벡터에 대한 외부 곱을 전체 대수로 확장하는 것은 일반적인 관행이다.이는 위에서 언급한 등급 투영 연산자를 사용하여 수행할 수 있습니다.
- : 、 r 、 + \ C \ D : = \ \ \ _ { \ _ { \ _ { s }( 외부 제품)
이 일반화는 반대칭화를 포함한 위의 정의와 일치한다.외부 제품과 관련된 또 다른 일반화는 정류자 제품입니다.
- × : ( - )( C \ D : = tfrac { ( } (정류자 제품)
회귀적(일반적으로 "만남"이라고 함)은 외부적(또는 이 [f]문맥에서 "가입")의 이중입니다.A(디스플레이 A및 B 의 경우 요소의 이중 사양에 따라 A A 및 B결합)[14]를 포함하는 최소 등급 블레이드에 대해 이중성이 요구되는 교차점(또는 충족)이 허용됩니다.
Idisplaystyle 단위 의사치수를 사용합니다.퇴행적인 제품은 외부 제품과 마찬가지로 [15]연관성이 있습니다.
벡터의 내적 또한 일반화 될 수 있지만, 하나 이상의 방법으로 동등하지 않다.논문(Dorst 2002)은 기하학적 대수와 그 상호 관계를 위해 개발된 여러 가지 다른 내부 산물에 대한 완전한 처리를 제공하며, 여기서 표기를 취한다.많은 저자가 선택한 확장에 대해 벡터의 내적과 동일한 기호를 사용한다(예: 헤스틴과 페르와스).일관된 표기법은 나타나지 않았다.
벡터에 대한 내부 곱의 몇 가지 다른 일반화 중 하나는 다음과 같다.
- sum \{r}\_{}(왼쪽 수축)
- sum \r}\}\_{오른쪽 수축)
- : , s、 r ⟩ 0 ( \ * D : = \ _ { , } \scarle \ _ {} \ cargle_ { 0) 。
- : , s、 s - - r、 \_ { , } \ C \ { r } \ D \ rangle _ { } \ _ { \ ( dot product [g])
도스트(2002)는 헤스틴의 내적보다 수축의 사용에 대한 주장을 펴고 있다. 그들은 대수적으로 더 규칙적이고 더 명확한 기하학적 해석을 가지고 있다.수축이 포함된 많은 정체성은 입력의 제한 없이 유효하다.예를들면,
벡터 상에서 왼쪽 축소를 내부 곱의 확장으로 사용하는 이점에는 A에 대해 b+ \ \ b + \ b가 B \ = a \ ; \ + b \로 확장된다는 것이 포함된다. 그리고 투영 Pb() ( b- )b {)=( b가 P ( ( -) ({ b - 1) {\display B (A } {cal_cal} {cal} {cal { {cal} {cal} {cal} b} {cal} b} {cal} b} b} {cal} {cal}로 확장아래에 표시된 한 B B에 맞게 약간 수정됨)
선형 함수
versor는 대수에서 멀티벡터로 직접 나타낼 수 있기 때문에 작업하기 더 쉽지만, versor는 멀티벡터에서 선형 함수의 하위 그룹이며 필요할 때 계속 사용할 수 있습니다.의{\ n차원 벡터 공간의 기하학적 대수는 의{\ 2개의 에 의해 확장됩니다.멀티벡터가 대수의 기초 의 ×1(\}\1)의 실제 열 행렬로 표현되는 경우 멀티벡터의 모든 선형 변환은 × 2 2의 실제 행렬로 표현될 수 있다.그러나 이러한 일반적인 선형 변환은 명확한 기하학적 해석이 없는 벡터로 스칼라의 "회전"과 같은 등급 간의 임의 교환을 허용합니다.
벡터에서 벡터로의 일반적인 선형 변환이 흥미롭다.유도 외부 대수를 보존하는 것에 대한 자연스러운 제한으로, 선형 변환의 외형성은 베르사의 고유한[h] 확장이다.ff가 벡터를 벡터에 매핑하는 선형 함수인 경우, 외형성은 규칙을 따르는 함수입니다.
선형성을 통해 전체 대수까지 확장됩니다.
지오메트리 모델링
비록 CGA에 많은 관심이 집중되었지만, GA는 단지 하나의 대수가 아니라 동일한 [16]필수 구조를 가진 대수군 중 하나라는 점에 주목해야 한다.
벡터 공간 모형
(, 0) { \ { ()는 벡터 대수의 확장 또는 완료로 간주할 수 있습니다.벡터부터 기하학 대수까지 기본 해석 기하학을 다루고 입체 [17]투영법을 소개합니다.
G 의 부분대수({ {G}}(2는 성분별로 벡터 P({를 직교 기준으로 쓰고, 왼쪽 ({을 곱하면 알 수 있듯이 복소수와 동형이다.
여기서 i i} 를 합니다.
로 {1 e3, e3 } }, } {2} 의G(의 짝수 부분 대수는 다음과 같습니다. " - e1 { j \ - e k k k k \ mapsto - e _ { } 、 " - \ k \ - _ {_ {2}} 。
모든 연관대수는 행렬표현이 있다. 세 데카르트 기저 벡터를 파울리 행렬로 대체하면 G( ,){ 의 이 된다.
- 와 b 및 b({ b})를 사용하여= 1 + e 2 + e 3 \ display style \ _ { {11} + \ _ 2_} + \ scapter {3 e {3} with with with with multip multip multip multip multip multip = multip multip multip = = = = = = = multip =
- ) ( b) + \ style ( \ style \ a ) \ b + \ \ b ) = a\ cdot b + \ b( \ b ) ( 。
시공간 모형
물리학에서 주요 응용 분야는 시공간(STA[3]이라 불리는 민코프스키 3+1 시공간의 기하학적 대수 G(1 3) 물리적 공간()의를 해석하는 G 이다.
STA에서는 시공간 점이 단순히 벡터로 표현되지만, APS에서는 ( 차원 시공간 점이 대신 파라벡터, 3차원 벡터(공간)와 1차원 스칼라(시간)로 표현된다.
시공간 대수에서 전자기장 텐서는 F ( + B ) 0{ { } =e E } + ic { _[18]이다.서 0 1 2 3{ i = \ _ { } \ _ { 0 }은 pseudoscalar ( 4차원 볼륨 요소이고 { \ _은 방향의 단위 벡터입니다c 및 자기장 벡터(제로 시간 성분 포함)입니다.4개의 J({style {를 사용하여 Maxwell의 방정식은
공식화 균질 방정식 비균질 방정식 필드 전위(모든 게이지) 전위(로렌츠 게이지)
기하학적 미적분학에서 D와 같은 벡터의 병렬배치는 기하학적 곱을 나타내며, F D F+ D F D ~ F + D \ ~ F + D \ F ( DF ~ F + D \ wedGE F ) here be as as as as as as as as as d d d d here here here here here here here here d d here d d d을(를) 평탄한 시공간에서 사용합니다.여기서 ({은 4({4})에서 역할을 합니다. 이는 3(\3)의 역할과 동의어이며 ◻= 의 달랑 관련이 있습니다n 옵서버는 미래 포인팅 타임라이크 0을 나타냅니다.
이 로렌츠 측정 공간에서의 부스트는 β e의 (\displaystyle e^{\beta})와 동일하며, 서β(\는 시간과 공간 방향에 의해 생성된 바이벡터이며, 유클리드에서는 두 공간 방향에 의해 생성된 바이벡터이다.거의 정체성에 대한 "유행"을 하고 있습니다.
Dirac 행렬은 G(,)의으로 물리학자들이 사용하는 행렬 표현과 동등함을 보여줍니다
균질 모형
투영 기하학 대수(PGA)는 균질 모형으로도 알려져 있으며, 모든 유클리드 등각체와 그것들이 동작하는 선형 부분 공간의 표현을 포함하는 완전한 대수학을 제공한다.이 모델에서는 공간의 n개의 통상적인 치수에 1개의 축퇴 치수를 더하여 G 1를 형성한다.G( 1)의 인 처리는 Lengyel에 [19]의해 .3차원 PGA에서는 벡터는 점, 바이벡터는 선, 트라이벡터는 평면에 대응한다.3D 공간에서 항상 나사 운동인 적절한 유클리드 등각은 8개의 짝수 등급 성분으로 구성된 모터로 표현되며, 반사를 포함하는 부적절한 유클리드 등각은 8개의 홀수 등급 성분으로 구성된 플렉터로 표현된다.모터 대수는 PGA에 나타나는 전체 개체 집합에 대한 이중 4분의 1의 올바른 일반화입니다.
PGA의 중심 개념은 물체의 각 구성요소에 존재하거나 존재하지 않는 기저 벡터의 반전을 통해 발생하는 대칭성입니다.이는 대수의 기하학적 객체에서 기본적인 이중성을 야기할 뿐만 아니라, 그 객체들에 대한 연산도 야기한다.대수의 모든 곱(웨지 곱, 내적, 기하 곱, 내적)은 피연산자의 이중에 대해 동일한 연산을 수행하는 일치하는 "반제품"을 가진다.대수를 완성하기 위해서는 두 가지 유형의 곱을 모두 포함하는 것이 필수적이다.쐐기곱과 그 듀얼인 안티웨지곱에 의해 다양한 형상간의 결합 및 결합 연산이 각각 이루어진다.벌크 노름과 체중 노름이라고 불리는 두 가지 다른 규범이 내적과 그 이중에 의해 주어지고, 이것들은 각각 스칼라와 반비늘 양을 생산한다.유클리드 등각성은 기하학적 반생산에 의해 수행된다.
투영 기하학 대수의 모든 개체는 투영되지 않은 설정에서 단순히 스칼라일 뿐인 크기를 포함하여 균질합니다.점, 선, 평면, 모터 또는 플렉터에 0이 아닌 스칼라를 곱해도 의미에 영향을 주지 않습니다.오브젝트는 유닛화라고 불리는 프로세스를 통해 3D 공간에 투영됩니다.이 프로세스를 통해 컴포넌트의 집합 크기가 퇴화 차원 통일성으로 확장됩니다.구체적인 거리 측정은 벌크 노름과 무게 노름의 합계인 기하학적 노름에 의해 주어진 균질한 크기로 발생한다.기하학적 노름이 단위화되면 스칼라 성분은 실제 거리를 나타냅니다.
등각 모형
GA 내에서 작업할 때, 유클리드 에서의 등각점과 함께은 CGA )에 투영적으로 삽입된다 CGA 서브벡터의 4D 원뿔에서 1D 부분공간으로 유클리드 점을 식별한다.이를 통해 모든 컨포멀 변환을 회전 및 반사로 수행할 수 있으며 공변성이므로 투영 형상의 발생 관계를 원과 구로 확장합니다.
구체적으로는직교 기저 e+(\와e-와 - -(\ =-을 G를 하는 벡터 공간의 기저에 합니다(\0 및 null 벡터 식별
- -++ (\ }= 무한대의 등각점(콤팩트화 참조) 및
- (e-+) ({ n _ { \ { o } = 1} {2 ( e _ { - } - e _ { +} ) 。
- o -({}}=-
이 절차는 투영 기하학에서 동종 좌표를 사용하는 절차와 몇 가지 유사하며, 이 R을 집합인변환으로 모델링할 수 있습니다
GA의 빠르게 변화하고 유동적인 영역인 CGA도 상대론적 물리학에 적용하기 위해 연구되고 있습니다.
투영적 변환 모델
두 잠재적인 후보 현재 조사를 받고, 사영 아핀 기하학을 3차원 R(3,3){\displaystyle{{R\mathcal}}(3,3)에 재단이다.}[20]and R({\displaystyle{{R\mathcal}}(는 무게가 4,4)}[21]포함된다 표현 시 가위와 불균등 스케일링뿐만 아니라 2차 곡면 surfaces원뿔형 섹션이 있습니다.
새로운 연구 모델인 쿼드릭 컨포멀 지오메트리 대수(QCGA) ( ({는 4차원 표면 전용 CGA의 확장입니다.그 아이디어는 대수의 저차원 부분 공간에서 객체를 표현하는 것이다.QCGA는 제어점 또는 암묵적 방정식을 사용하여 4차원 표면을 구성할 수 있습니다.또한 QCGA는 4차원 [22]표면에 있는 점에서의 표면 접선 및 법선 벡터뿐만 아니라 4차원 표면의 교차점도 계산할 수 있습니다.
기하학적 해석
투영 및 거부
a및 벡터에 대해
여기서m 평행 부분)에 대한 a의 투사(또는 평행 부분)
m 직교 부분)에서 {\ a가 거부되면
V의 을 나타내는k K B V의 개념을 사용하여 최종적으로 벡터로 표현되는 모든 멀티벡터를 k(\k) B(\ B에 투영하는 일반 멀티벡터입니다.로서[i]
거부반응이 로 정의되면서
투영 및 제거는 수축 [j]제품에 대해 역 - B을 의사 B+({ B로 대체함으로써 늘 B({ B로 일반화됩니다.투영 결과는 Null이 아닌 [23][24]블레이드에 대해 두 경우 모두 일치합니다. 블레이드의 경우 여기서 주어진 투영에 대한 [k]정의를 의사 역방향의 두 번째가 아니라 첫 번째 수축으로 사용해야 합니다. 이때만[23]로 표현되는 부분 공간에서 결과가 반드시 나타나기 때문입니다.투영법은 선형성을 통해 일반 A A[l]로 일반화됩니다.투영은 B B에서 선형적이지 않으며 가 아닌 B( 스타일 B로 일반화되지 않습니다.
반사
초평면에서의 단순한 반사는 단일 벡터와의 결합을 통해 대수에서 쉽게 표현된다.이것들은 일반적인 회전과 회전의 그룹을 생성하는 역할을 합니다.
c {\ c의 벡터m {\ m에 따른 c{\ c 또는 m{\m에 직교하는 하이퍼플레인에서의 반사 c {\displaystyle m는 m{\ m에 평행한 벡터의 성분을 부정하는 것과 같습니다.반성의 결과는 다음과 같습니다.
은 치수 n n 4일 때 반사라고 볼 수 있는 가장 일반적인 연산은 아닙니다. 일반 반사는 홀수 개수의 단일 축 반사를 합친 것으로 나타낼 수 있습니다. 벡터의 일반 a가 기록될 수 있습니다.
어디에
- r{ M\r } 및 - ( - ) - - p - ( \ r - 1 } =^{ - 1= r ( \ r } }
벡터 곱의 비늘 m m에 따른 반사를 동일한 벡터에 따른 제품 내의 모든 벡터의 반사로 정의하면, 예를 들어 다음과 같은 홀수 수의 벡터의 곱에 대해 얻을 수 있다.
짝수 벡터의 곱에 대해서
모든 멀티벡터가 궁극적으로 벡터로 표현된다는 개념을 사용하여 반사 버스터을 사용하는 일반 AA의 반사를 기록할 수 있다.
서α {\는 전체 대수까지 선형성을 통해 확장된 벡터 공간(δ - {\ v -v의 원점을 통한 반사의 자기동형성이다.
회전수
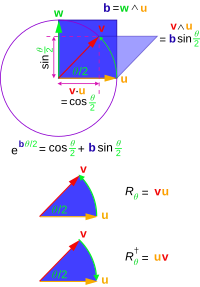
R a R의 곱이 있는 경우, 그 역수를 다음과 같이 나타냅니다.
예를 들어, b{ Rab }라고 가정합니다.
R이 1(\ RR}}이 R R)을 합니다.
R R~ {\ Rv는v {\ v의 를 변경하지 않습니다.그리고 또 다른 것도 보여줄 수 있어요
따라서 R R~ {\ Rv {R는 길이와 각도를 모두 유지합니다.따라서 회전 또는 회전으로 식별할 수 R {\ R은 적절한 회전(짝수 벡터의 곱으로 표현될 수 있는 경우)이면 회전자(roter)라고 하며, GA에서 Versor라고 하는 것의 한 예이다.
- / ( \ R = { - \ ) 의 멀티벡터 형성과 관련된 벡터를 평면 내에서 2( \ 2) B(\ 2)에 의해 정의된 방향으로 회전시키는 일반적인 방법이 있다.
회전 장치(Roter는 4차원 공간을 n( n으로 일반화한 것입니다.
베르소르
k -versor는 k(\ k 반전 [m][26]벡터의 곱으로 표현될 수 있는 멀티벡터입니다.유닛 쿼터니언(원래 Hamilton에 의해 버서라고 불림)은 실제 2D 로터가 복잡한 숫자를 포함하는 것과 거의 동일한 방법으로 3D 공간의 로터와 식별할 수 있습니다. 자세한 내용은 [27]도스트를 참조하십시오.
일부 저자는 연산자 간에 피연산자가 "샌드위칭"되는 자주 발생하는 경우를 언급하기 위해 "versor product"라는 용어를 사용한다.회전과 반사에 대한 설명(외형성 포함)은 이러한 샌드위치화의 예입니다.이 외형들은 특히 단순한 대수적 [n]형태를 가지고 있다.특히, 형식의 벡터 매핑은
- : a R-1 ( \ \ RaR ^ { - map to RaR^ { - } ) G () : A - .{ \ { } ( } { cal }
연산자와 피연산자 모두 버서이기 때문에 이러한 연산에 기하학적 또는 물리적 중요성을 부가할 수 있다면 회전자를 회전시키거나 스피너를 반사하는 것과 같은 대체 예가 될 가능성이 있다.
카르탄-디오도네 정리에 따르면 모든 등각은 초평면에서 반사로 주어질 수 있으며, 합성 반사가 회전을 제공하므로 직교 변환은 베르사르이다.
용어로 표현하면, 그룹G× (\}})를의 가역 요소 군으로 식별한 displaystyle { times}} {\times}} {displaystyle {\mathcal }}}룬드홀름은 1의 를 증명한다. v k: v i} ×} { \ {{ { } \ v _ { k } \ { \ times} \} (역버서 집합)는 립시츠 그룹 }a.k.a. \ \ \ gamma} Cliffma 그룹과 동일합니다
δ의 서브그룹
Lundholm은 벡터에 의해 생성되는 핀 {Spin 및 서브그룹을 합니다. [29]짝수 벡터 팩터만 존재할 수 있습니다.
| 서브그룹 | 정의. | 묘사 |
|---|---|---|
| 유닛 버스터 | ||
| 짝수 단위 버서 | ||
| 로터 |
스피너는 실제 GA의 짝수 하위 대수의 요소로 정의됩니다. 스피너에 대한 GA 접근법의 분석은 Francis와 Kosowsky에 [30]의해 제공됩니다.
예와 응용 프로그램
벡터에 의해 확장된 병렬 동위원소의 하이퍼볼륨
을 가로지르는 와경우
결과 평행사변형의 "와 "근거의 곱, 즉 면적에서 이다.
{\ n 차원 병렬 도토프에 걸친 벡터 수에도 동일한 해석이 적용됩니다 즉, n ldots, 의 외부 곱, 즉 i {\{1_i}^{ {n} {n} {n} {n} {n}{n} {n} {n} {n} {n} {n}에 걸쳐 있습니다.는n\n-display 의 부피와 같습니다.nn-벡터의 이 반드시 평행동위원소일 필요는 없습니다.이것은 편리한 시각화입니다.부피가 평행동위원소의 부피와 같긴 하지만, 어떤 모양이든 될 수 있습니다.
선과 평면의 교차
p + { p \로 라인을 파라미터로 정의할 수 있습니다. 서p { p와 t{ t는 점 P와 T의 위치 이고 v{ v는 라인의 방향 벡터입니다.
그리고나서
- ( - ) { B \ ( p - q ) = + -q ) { B \ (+ \ v - q ) =}
그렇게
그리고.
회전 시스템
토크와 각운동량과 같은 회전력에 대한 수학적인 설명은 방향(손잡이)의 규칙과 함께 3차원의 벡터 미적분의 교차곱을 사용하는 경우가 많다.
교차곱은 외부 곱의 관점에서 볼 수 있으므로 이중 관계를 사용하여 교차곱을 이중 벡터로 보다 자연스럽게 기하학적으로 해석할 수 있습니다.
예를 들어, 토크는 일반적으로 수직력 성분의 크기에 거리를 곱한 값 또는 단위 각도당 작용으로 정의됩니다.
직교 정규 u v {\을(를) 포함하는 임의 평면 내의 원형 경로가 각도로 매개 변수화된다고 가정합니다.
이 평면의 단위 바이벡터를 허수로 지정함으로써
이 경로 벡터는 복잡한 지수 형식으로 편리하게 쓰여질 수 있다
그리고 각도에 대한 미분은
토크 즉 힘 F 스타일F)에 의한 변화율W(\ W는
토크의 교차곱 기술인 r × {\ =\} \ F와 달리 기하학적 대수 기술은 정규 방향의 벡터를 도입하지 않는다. 즉, 2차원 이상에서 고유하지 않은 벡터이다.유닛 바이벡터는 회전의 평면과 방향을 나타내며 회전감은 u 와 v 사이의 각도에 비례합니다.
기하학 미적분
기하학 미적분은 미분 기하학과 미분 [31]형태를 포함한 미분과 적분을 포함하도록 형식주의를 확장한다.
본질적으로, 벡터 도함수는 GA 버전의 그린 정리가 참이 되도록 정의된다.
그러면 글을 쓸 수 있다.
기하학적 곱으로서 스토크스의 정리를 효과적으로 일반화한다(그 미분 형식 버전 포함).
A디스플레이 스타일 A가 a a)와 b b를 가진 곡선일 ,
으로 줄이다
또는 적분학의 기본 정리입니다.
또한 벡터 다양체의 개념과 기하학적 적분 이론(미분 형식을 일반화)이 발전되었다.
역사
- 20세기 이전
비록 기하학과 대수학의 연관성은 적어도 기원전 3세기 유클리드의 원소까지 거슬러 올라가지만, 이 기사에서 사용된 의미의 GA는 공간의 기하학적 특성과 변환을 설명하는 체계적 방법으로 사용된 1844년까지 개발되지 않았다.그 해에 헤르만 그라스만은 공간의 [32]모든 기하학적 정보를 부호화한 특정 미적분으로서 완전한 일반성의 기하학적 대수 개념을 도입했다.그래스만의 대수체계는 유클리드 공간, 아핀 공간, 사영 공간 등 여러 종류의 공간에 적용될 수 있다.그래스만에 이어 1878년 윌리엄 킹든 클리포드는 (클리퍼드 오류에서 윌리엄 로완 해밀턴의 4원소와 함께 그래스만의 대수 체계를 조사했다: 없음: 1878 그의 관점에서, 4분의 1은 특정한 변화를 기술했고, 그라스만의 대수는 특정한 특성(또는 길이, 면적, 부피와 같은 Strecken)을 기술했다.그의 공헌은 기존의 그래스만 대수에 새로운 곱, 즉 기하학적 곱을 정의하는 것이었는데, 그것은 사분위수가 그 대수 안에 산다는 것을 깨달았다.이후 1886년 루돌프 립시츠는 클리포드의 사분위수 해석을 일반화해n차원 기하학에 적용했다.나중에 이러한 발전은 다른 20세기 수학자들이 클리포드 대수의 특성을 공식화하고 탐구하도록 이끌 것이다.
그럼에도 불구하고, 19세기의 또 다른 혁명적 발전은 기하학적 대수학을 완전히 무색하게 할 것이다: 조시아 윌러드 깁스와 올리버 헤비사이드에 의해 독립적으로 개발된 벡터 해석의 그것이다.벡터 분석은 James Cluck Maxwell의 전자기학 연구, 특히 특정 미분 방정식을 편리하게 표현하고 조작할 필요성에 의해 동기 부여되었습니다.벡터 분석은 새로운 대수의 엄격함에 비해 특정한 직관적인 매력을 가지고 있었다.물리학자들과 수학자들 모두 깁스의 강의에 이어 1901년 에드윈 비드웰 윌슨이 쓴 영향력 있는 교과서 벡터 분석의 뒤를 이어 그것을 그들의 기하학적 도구 모음으로 쉽게 채택했다.
좀 더 자세히 말하자면, 기하학 대수에 대한 세 가지 접근법이 있다: 1843년 해밀턴에 의해 시작되었고 1878년 클리포드에 의해 로터로서 기하학 대수가 되었다; 1844년 그래스만에 의해 시작된 기하학 대수와 19세기 후반 깁스와 헤비사이드에 의해 4차원 해석에서 발전되었다. 분석에서 분석의 유산은 R의 벡터를 나타내기 위해 i 를 하는 것에서 알 수 있다 : 하게 상상의 4분위 분석으로 생각되고 있다.기하학적 대수의 관점에서, 공간 대수의 짝수 부분 대수는 3D 유클리드 공간의 GA와 동형이며, 4분의 1은 3D 유클리드 공간의 GA의 짝수 부분 대수와 동형이다.
- 20세기 및 현재
클리포드 대수의 연구는 20세기 동안 조용히 진전되었지만, 주로 엘리 카르탕, 헤르만 바일, 클로드 체발리와 같은 추상 대수학자들의 연구 덕분이었다.기하학적 대수에 대한 기하학적 접근법은 20세기의 많은 부활을 보았다.수학에서, 에밀 아르틴의 기하학[33] 대수학은 아핀 기하학, 투영 기하학, 심플렉틱 기하학, 직교 기하학을 포함한 여러 기하학과 관련된 대수학을 논한다.물리학에서 기하학 대수는 양자역학이나 게이지 [5]이론과 같은 보다 진보된 주제와 함께 고전 역학과 전자기학을 하는 "새로운" 방법으로 부활했다.데이비드 헤스테네스는 파울리와 디락 행렬을 각각 일반 공간과 시공간에서 벡터로 재해석했고 기하학 대수학의 주요 현대 주창자였다.
컴퓨터 그래픽과 로봇 공학에서는 회전과 다른 변환을 효율적으로 표현하기 위해 기하학 대수가 부활했다.로봇 공학(나사 이론, 버스터를 이용한 운동학 및 역학), 컴퓨터 비전, 제어 및 신경 컴퓨팅(기하학 학습)에 GA를 적용하는 방법은 Bayro(2010)를 참조하십시오.
「 」를 참조해 주세요.
메모들
- ^ 기하학 대수학에서 사용되는 외적이라는 용어는 수학의 다른 곳에서 외적의 의미와 충돌한다.
- ^ 2 { u} 、 ( ( +) 2 ( \ { {2 ) (1 + ) 。 4( + u + =1 . 4(+ u + ) ( 1 + =1 ( + u + 1 ){ )( -) { { { ( +) ( - ) ( -) ( \ style ={ } ( 1 - u )1 、 0)
- ^ 이는 유사 유클리드 벡터 공간의 스칼라 곱의 동의어로, 규범 벡터 공간 상의 내부 곱이 1 {\1) - 벡터 부분 공간 상의 대칭 쌍선형 형태를 나타낸다.일부 저자들은 내부곱의 의미를 전체 대수학으로 확장할 수 있지만, 이에 대한 합의는 거의 없다.심지어 기하학 대수에 관한 텍스트에서도 이 용어는 보편적으로 사용되지 않는다.
- ^ 기하학적 곱에 따른 등급을 언급할 때, 문헌은 일반적으로 및 Z 등급으로 분할된 Z 2 \mathrm 에만 초점을 맞추고 있습니다.는 기하학적 곱의 의 부분군이다.
- ^ Grade는 Grading 아래의 균질한 요소의 정도와 동의어로 외부 곱과의 대수(Z \-grading)로서 곱이 [d]아니다.
- ^ [...] 외부 제품 작동과 결합 관계는 기본적으로 동일한 의미를 가집니다.Grassmann-Cayley 대수는 미트 관계를 그것의 대항어로 간주하고 이 두 연산이 동등한 기반을 갖는 통합 프레임워크를 제공한다 [...] 그라스만 자신은 미트 연산을 외적 연산의 쌍으로 정의했지만, 이후 수학자들은 프로세서를 통해 미트 연산자를 외적으로부터 독립적으로 정의했다.shuffle이라고 불리며, meet 조작은 shuffle product라고 불립니다.이것은 연관성을 만족시키는 반대칭 연산이며, 그 자체로 대수를 정의한다.따라서, 그래스만-케일리 대수는 동시에 두 개의 대수 구조를 갖는다. 하나는 외부 곱(또는 결합)에 기초하고 다른 하나는 셔플 곱(또는 충족)에 기초한다.따라서 "이중 대수"라는 명칭과 이 둘은 서로 [13]쌍대수임을 알 수 있다.
- ^ 이것은 Hestenes의 불규칙한 C D : 、 0 D - \ \ _ { \ { }와 혼동해서는 안 됩니다. _ 0 0_{ D_{ _ 여기서 식별표기는 Dorst, Fontijne & Mann(2007)의 590을 나타냅니다.
- ^ 일반적으로 제로 맵의 고유성을 보장하기 위해 f _() ( { \ { } =1이라는 을 추가합니다.
- ^ 이 정의는 Dorst(2007) 및 Perwass(2009)가 사용하는 왼쪽 수축은 Perwass가 하는 내부 제품뚱한점을 대체하여을 할 수 없다는 Perwass의 제약 조건과 일치합니다.
- ^ Dorst는 단순히B+ (\ B라고 가정하는 반면, Perwass(2009)는B + B /( † B †† B ) (\ )라고 한다.B표시 B를 먹은 것으로 표시까지 B B의 역행과 동일합니다.
- ^ 즉, 투영은 P () (B+ )B (\ (A) = (A\;B} 로 되어야 하며 ( 로 정의해서는 안 됩니다
- ^ 모든에 대한 이 일반화는 Perwass나 Dorst에 의해 고려되지 않은 것 같습니다.
- ^ "사용되지 않게 된 해밀턴의 4분의 1 미적분으로부터 용어를 부활시켜 일반화" 는 k[25] k 벡터의 에 인수분해할 수 있는 멀티벡터로 kdisplaystyle k-versor를 정의했다.
- ^ 2차 형식을 존중하는 선형 변환의 외형만이 이 설명에 들어맞는다; 외형식은 일반적으로 대수 연산으로 표현될 수 없다.
인용문
- ^ 헤스틴 1986, 페이지 6
- ^ Li 2008, 페이지 411
- ^ a b 헤스틴 1966년
- ^ 헤스틴즈 2003.
- ^ a b 도란 1994년
- ^ Lasenby, Lasenby & Doran 2000.
- ^ 힐든브랜드 외 2004년.
- ^ 헤스틴 & 삭지크 1984, 3-5페이지
- ^ 아라곤, 아라곤 & 로드리게스 1997, 페이지 101
- ^ a b 헤스틴스, 데이비드 (2005), 기하학 대수 입문
- ^ Penrose 2007.
- ^ Wheeler & Misner 1973, 페이지 83. 오류:: (
- ^ 카나타니 2015, 페이지 112-113
- ^ Dorst & Lasenby 2011, 페이지 443.
- ^ Vaz & da Rocha 2016, 2.8파운드.
- ^ Dorst & Lasenby 2011, 페이지 vi.
- ^ Ramirez, Gonzalez & Sobczyk 2018.
- ^ "Electromagnetism using Geometric Algebra versus Components". Retrieved 2013-03-19.
- ^ Lengyel, Eric. "Projective Geometric Algebra Wiki".
- ^ 도스트 2016.
- ^ Juan Du, Ron Goldman, Stephen Mann (December 2017). "Modeling 3D Geometry in the Clifford Algebra R(4,4)". Advances in Applied Clifford Algebras. 27 (4): 3039–3062. doi:10.1007/s00006-017-0798-7. S2CID 126166668.
{{cite journal}}: CS1 maint: 작성자 파라미터 사용(링크) - ^ Breuils, Stéphane (17 December 2018). Structure algorithmique pour les opérateurs d'Algèbres Géométriques et application aux surfaces quadriques (PDF) (PHD). université-paris-est.
- ^ a b Dorst 2007, § 3.6 p. 85. 오류:: (도움말
- ^ 2009년 기준, § 3.2.10.2 p. 83.
- ^ 헤스틴 & 삭지크 1984, 페이지 103
- ^ Dorst 2007, 페이지 204. 오류:: 2007
- ^ Dorst 2007, 페이지 177–182. 오류:: (도움말
- ^ Lundholm & Svensson 2009, 페이지 58 et seq.
- ^ 룬드홀름 & 스벤슨 2009, 58페이지
- ^ Francis & Kosowsky 2008.
- ^ 헤스틴 & 소브지크 1984.
- ^ 그라스만 1844년
- ^ Artin 1957. 오류::
참고 자료 및 추가 자료
- 시간순으로 배열됨
- Grassmann, Hermann (1844), Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik: dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert, Leipzig: O. Wigand, OCLC 20521674
- Artin, Emil (1988) [1957], Geometric algebra, Wiley Classics Library, Wiley, doi:10.1002/9781118164518, ISBN 978-0-471-60839-4, MR 1009557
- Hestenes, David (1966), Space–time Algebra, Gordon and Breach, ISBN 978-0-677-01390-9, OCLC 996371
- Wheeler, J. A.; Misner, C.; Thorne, K. S. (1973), Gravitation, W.H. Freeman, ISBN 978-0-7167-0344-0
- Bourbaki, Nicolas (1980), "Ch. 9 "Algèbres de Clifford"", Eléments de Mathématique. Algèbre, Hermann, ISBN 9782225655166
- Hestenes, David; Sobczyk, Garret (1984), Clifford Algebra to Geometric Calculus, a Unified Language for Mathematics and Physics, Springer Netherlands, ISBN 9789027716736
- Hestenes, David (1986), J.S.R. Chisholm; A.K. Commons (eds.), "A Unified Language for Mathematics and Physics", Clifford Algebras and Their Applications in Mathematical Physics, NATO ASI Series (Series C), Springer, 183: 1–23, doi:10.1007/978-94-009-4728-3_1, ISBN 978-94-009-4728-3
- Doran, Chris J. L. (1994), Geometric Algebra and its Application to Mathematical Physics (PhD thesis), University of Cambridge, doi:10.17863/CAM.16148, hdl:1810/251691, OCLC 53604228
- Baylis, W. E., ed. (2011) [1996], Clifford (Geometric) Algebra with Applications to Physics, Mathematics, and Engineering, Birkhäuser, ISBN 9781461241058
- Aragón, G.; Aragón, J.L.; Rodríguez, M.A. (1997), "Clifford Algebras and Geometric Algebra", Advances in Applied Clifford Algebras, 7 (2): 91–102, doi:10.1007/BF03041220, S2CID 120860757
- Hestenes, David (1999), New Foundations for Classical Mechanics (2nd ed.), Springer Verlag, ISBN 978-0-7923-5302-7
- Lasenby, Joan; Lasenby, Anthony N.; Doran, Chris J. L. (2000), "A Unified Mathematical Language for Physics and Engineering in the 21st Century" (PDF), Philosophical Transactions of the Royal Society A, 358 (1765): 21–39, Bibcode:2000RSPTA.358...21L, doi:10.1098/rsta.2000.0517, S2CID 91884543
- Baylis, W. E. (2002), Electrodynamics: A Modern Geometric Approach (2nd ed.), Birkhäuser, ISBN 978-0-8176-4025-5
- Dorst, Leo (2002), "The Inner Products of Geometric Algebra", in Dorst, L.; Doran, C.; Lasenby, J. (eds.), Applications of Geometric Algebra in Computer Science and Engineering, Birkhäuser, pp. 35–46, doi:10.1007/978-1-4612-0089-5_2, ISBN 978-1-4612-0089-5
- Doran, Chris J. L.; Lasenby, Anthony N. (2003), Geometric Algebra for Physicists (PDF), Cambridge University Press, ISBN 978-0-521-71595-9
- Hestenes, David (2003), "Oersted Medal Lecture 2002: Reforming the Mathematical Language of Physics" (PDF), Am. J. Phys., 71 (2): 104–121, Bibcode:2003AmJPh..71..104H, CiteSeerX 10.1.1.649.7506, doi:10.1119/1.1522700
- Hildenbrand, Dietmar; Fontijne, Daniel; Perwass, Christian; Dorst, Leo (2004), "Geometric Algebra and its Application to Computer Graphics" (PDF), Proceedings of Eurographics 2004, doi:10.2312/egt.20041032
- Bain, J. (2006), "Spacetime structuralism: §5 Manifolds vs. geometric algebra", in Dennis Dieks (ed.), The ontology of spacetime, Elsevier, p. 54 ff, ISBN 978-0-444-52768-4
- Dorst, Leo; Fontijne, Daniel; Mann, Stephen (2007), Geometric algebra for computer science: an object-oriented approach to geometry, Elsevier, ISBN 978-0-12-369465-2, OCLC 132691969
- Penrose, Roger (2007), The Road to Reality, Vintage books, ISBN 978-0-679-77631-4
- Francis, Matthew R.; Kosowsky, Arthur (2008), "The Construction of Spinors in Geometric Algebra", Annals of Physics, 317 (2): 383–409, arXiv:math-ph/0403040v2, Bibcode:2005AnPhy.317..383F, doi:10.1016/j.aop.2004.11.008, S2CID 119632876
- Li, Hongbo (2008), Invariant Algebras and Geometric Reasoning, World Scientific, ISBN 9789812770110. PDF로서의 제1장
- Vince, John A. (2008), Geometric Algebra for Computer Graphics, Springer, ISBN 978-1-84628-996-5
- Lundholm, Douglas; Svensson, Lars (2009), "Clifford Algebra, Geometric Algebra and Applications", arXiv:0907.5356v1 [math-ph]
- Perwass, Christian (2009), Geometric Algebra with Applications in Engineering, Geometry and Computing, vol. 4, Springer Science & Business Media, Bibcode:2009gaae.book.....P, doi:10.1007/978-3-540-89068-3, ISBN 978-3-540-89068-3
- Bayro-Corrochano, Eduardo (2010), Geometric Computing for Wavelet Transforms, Robot Vision, Learning, Control and Action, Springer Verlag, ISBN 9781848829299
- Bayro-Corrochano, E.; Scheuermann, Gerik, eds. (2010), Geometric Algebra Computing in Engineering and Computer Science, Springer, ISBN 9781849961080 http://geocalc.clas.asu.edu/html/UAFCG.html #5의 새로운 계산기하학과 나사이론의 회춘을 위한 도구에서 온라인으로 추출
- Goldman, Ron (2010), Rethinking Quaternions: Theory and Computation, Morgan & Claypool, Part III. Rethinking Quaternions and Clifford Algebras, ISBN 978-1-60845-420-4
- Dorst, Leo.; Lasenby, Joan (2011), Guide to Geometric Algebra in Practice, Springer, ISBN 9780857298119
- Macdonald, Alan (2011), Linear and Geometric Algebra, CreateSpace, ISBN 9781453854938, OCLC 704377582
- Snygg, John (2011), A New Approach to Differential Geometry using Clifford's Geometric Algebra, Springer, ISBN 978-0-8176-8282-8
- Hildenbrand, Dietmar (2013), Foundations of Geometric Algebra Computing, AIP Conference Proceedings, vol. 1479, pp. 27–30, Bibcode:2012AIPC.1479...27H, CiteSeerX 10.1.1.364.9400, doi:10.1063/1.4756054, ISBN 978-3-642-31793-4
- Bromborsky, Alan (2014), An introduction to Geometric Algebra and Calculus (PDF)
- Klawitter, Daniel (2014), Clifford Algebras: Geometric Modelling and Chain Geometries with Application in Kinematics, Springer, ISBN 9783658076184
- Kanatani, Kenichi (2015), Understanding Geometric Algebra: Hamilton, Grassmann, and Clifford for Computer Vision and Graphics, CRC Press, ISBN 9781482259513
- Li, Hongbo; Huang, Lei; Shao, Changpeng; Dong, Lei (2015), "Three-Dimensional Projective Geometry with Geometric Algebra", arXiv:1507.06634v1 [math.MG]
- Hestenes, David (11 April 2016). "The Genesis of Geometric Algebra:A Personal Retrospective". Advances in Applied Clifford Algebras. 27 (1): 351–379. doi:10.1007/s00006-016-0664-z. S2CID 124014198.
- Dorst, Leo (2016), 3D Oriented Projective Geometry Through Versors of , Springer, ISBN 9783658076184
- Vaz, Jayme; da Rocha, Roldão (2016), An Introduction to Clifford Algebras and Spinors, ISBN 978-0-19-878292-6
- Ramirez, Sergio Ramos; Gonzalez, Jose Alfonso Juarez; Sobczyk, Garrett (2018), "From Vectors to Geometric Algebra", arXiv:1802.08153v1 [math.GM]
- Bayro-Corrochano, Eduardo (2018). Computer Vision, Graphics and Neurocomputing. Geometric Algebra Applications. Vol. I. Springer. ISBN 978-3-319-74830-6.
- Lavor, Carlile; Xambó-Descamps, Sebastià; Zaplana, Isiah (2018). A Geometric Algebra Invitation to Space-Time Physics, Robotics and Molecular Geometry. Springer. pp. 1–. ISBN 978-3-319-90665-2.
- Josipović, Miroslav (22 November 2019). Geometric Multiplication of Vectors: An Introduction to Geometric Algebra in Physics. Springer International Publishing;Birkhäuser. p. 256. ISBN 978-3-030-01756-9.
외부 링크
- 아이오와주 루터칼리지, 앨런 맥도날드 기하학 대수 및 기하학 미적분 조사.
- 상상 속의 숫자는 실수가 아니다 – 시공간의 기하학적 대수이다.개요(Cambridge GA 그룹).
- Geometric Algebra 2015, Scientific Computing 석사 과정, 박사 과정크리스 도란(캠브리지).
- (게임) 프로그래머용 연산: 5 – 멀티벡터 방식.프로그래머를 위한 Ian Bell의 포괄적인 소개 및 레퍼런스.
- IMPA Summer School 2010 Fernandes Oliveira 소개 및 슬라이드.
- 후쿠이 E.S.M. 히처 대학과 일본 GA 출판물.
- 구글 그룹 for GA
- 기하학 대수 입문 GA, Jaap Suter 소개.
- 기하학 대수학 자료에서 위키의 큐레이터 파블로 블라이어입니다
- 2018년 컴퓨터 공학 조기진행에서 기하학 대수학을 적용
- GAME2020 기하학 대수학 미니 이벤트
- AGACSE 2021 비디오
초기 서적과 논문의 영어 번역
- G. 컴베비아크, "3쿼터 계산" (박사 학위 논문)
- M. Markic, "트랜스포머:새로운 수학 차량입니다.콤베바이악의 삼원소와 그라스만의 기하학적 시스템을 합성한 것입니다.사분위수의 미적분"
- C. Burali-Forti, "사영기하학에서의 그라스만법" 사영기하학에 외부대수를 적용하는 것에 관한 3개의 주석 편집
- C. Burali-Forti, "H. Grassmann의 방법에 따른 미분 기하학 입문" Grassmann 대수 적용에 관한 초기 책
- H. Grassmann, "연장이론의 원리에 따라" 외부대수의 응용에 관한 그의 논문 중 하나.
연구 그룹
- 국제 기하학 미적분학 협회전 세계 리서치 그룹, 소프트웨어 및 컨퍼런스 링크
- 캠브리지 기하학 대수군.전문 온라인 출판물 및 기타 자료.
- 암스테르담 대학교 그룹
- 기하학 미적분 연구 개발(아리조나 주립 대학).
- GA-Net 블로그 및 뉴스레터 아카이브.기하학 대수/클리퍼드 대수 개발 뉴스.
- 지각 작용 시스템을 위한 기하학적 대수학. 기하학적 사이버네틱스 그룹(CINVESTAV, 멕시코 과달라하라 캠퍼스).














 ID 요소(
ID 요소(





 대체되는 것을 제외하고 외부 제품의 특성은 동일합니다.
대체되는 것을 제외하고 외부 제품의 특성은 동일합니다. 음이 아닐 필요가 있습니다.기하학적 곱의 중요한 특성은 곱셈 역수를 가진 원소의 존재이다.
음이 아닐 필요가 있습니다.기하학적 곱의 중요한 특성은 곱셈 역수를 가진 원소의 존재이다.



 1})
1})













 정의된다.내부가
정의된다.내부가 






 벡터(대수의 일반 요소가 아님)이다.대수의 모든 원소는 이 형식의 곱의 합으로 표현될 수 있기 때문에, 이것은 대수의 모든 원소의 쌍에 대한 외부 곱을 정의한다.이는 외부곱이
벡터(대수의 일반 요소가 아님)이다.대수의 모든 원소는 이 형식의 곱의 합으로 표현될 수 있기 때문에, 이것은 대수의 모든 원소의 쌍에 대한 외부 곱을 정의한다.이는 외부곱이 

![{\displaystyle [\mathbf {A} ]_{ij}=a_{i}\cdot a_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5207597ca24e5f3fc11785e33dd676e5565e164f)

 의해
의해 대각화할 수 있다.
대각화할 수 있다.![\sum _{k,l}[\mathbf {O} ]_{ik}[\mathbf {A} ]_{kl}[\mathbf {O} ^{\mathrm {T} }]_{lj}=\sum _{k,l}[\mathbf {O} ]_{ik}[\mathbf {O} ]_{jl}[\mathbf {A} ]_{kl}=[\mathbf {D} ]_{ij}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c169d06e467c5c7959e7da65c5b01b1bb89a4d05)

![e_{i}=\sum _{j}[\mathbf {O} ]_{ij}a_{j}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb80eb1d95f0720fd0d25abff339a0aed390074e)
![e_{i}\cdot e_{j}=[\mathbf {D}]_{ij}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4620f4330bb5f5260c8978c2b7340df0c54f3725)
 기하학적 곱은 외부 곱에 의해 완전히 지정됩니다.
기하학적 곱은 외부 곱에 의해 완전히 지정됩니다.![{\displaystyle {\begin{array}{rl}e_{1}e_{2}\cdots e_{r}&=e_{1}\wedge e_{2}\wedge \cdots \wedge e_{r}\\&=\left(\sum _{j}[\mathbf {O} ]_{1j}a_{j}\right)\wedge \left(\sum _{j}[\mathbf {O} ]_{2j}a_{j}\right)\wedge \cdots \wedge \left(\sum _{j}[\mathbf {O} ]_{rj}a_{j}\right)\\&=(\det \mathbf {O} )a_{1}\wedge a_{2}\wedge \cdots \wedge a_{r}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/426956a7cc82e46726be135237774216bddee9f2)









 S
S





 스칼라라고 합니다.
스칼라라고 합니다.

 곱은 0
곱은 0
 등급 투영 연산자
등급 투영 연산자










 직교
직교



 I
I






 찾을 수 있으므로 단위
찾을 수 있으므로 단위 



 구성된 표준 베이스가 주어진 경우,
구성된 표준 베이스가 주어진 경우, 








 i
i














 P
P 실제
실제  실제
실제 

 성분별로 벡터 P({
성분별로 벡터 P({ 직교 기준으로 쓰고, 왼쪽
직교 기준으로 쓰고, 왼쪽 












 pseudoscalar (
pseudoscalar ( 방향의
방향의









 같은 벡터의 병렬배치는 기하학적 곱을 나타내며,
같은 벡터의 병렬배치는 기하학적 곱을 나타내며, 
 (를) 평탄한 시공간에서 사용합니다.여기서
(를) 평탄한 시공간에서 사용합니다.여기서 














 G를
G를 




 4차원 표면 전용 CGA의 확장입니다.그 아이디어는 대수의 저차원 부분 공간에서 객체를 표현하는 것이다.QCGA는 제어점 또는 암묵적 방정식을 사용하여 4차원 표면을 구성할 수 있습니다.또한 QCGA는 4차원
4차원 표면 전용 CGA의 확장입니다.그 아이디어는 대수의 저차원 부분 공간에서 객체를 표현하는 것이다.QCGA는 제어점 또는 암묵적 방정식을 사용하여 4차원 표면을 구성할 수 있습니다.또한 QCGA는 4차원 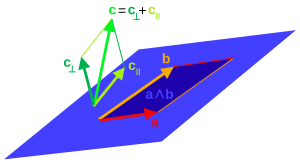


 이 평면에서의
이 평면에서의 






 의사
의사  대체함으로써 늘
대체함으로써 늘 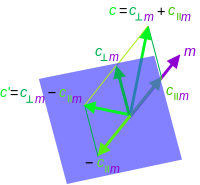










 전체 대수까지 선형성을 통해 확장된 벡터 공간(
전체 대수까지 선형성을 통해 확장된 벡터 공간(





 동일한 해석이 적용됩니다.
동일한 해석이 적용됩니다. 곱이 있는 경우, 그 역수를 다음과 같이 나타냅니다.
곱이 있는 경우, 그 역수를 다음과 같이 나타냅니다.


 1(\
1(\



 멀티벡터 형성과 관련된 벡터를 평면
멀티벡터 형성과 관련된 벡터를 평면 
















 라인을 파라미터로 정의할 수 있습니다.
라인을 파라미터로 정의할 수 있습니다.  점 P와 T의 위치
점 P와 T의 위치 





 (를) 포함하는 임의 평면 내의 원형 경로가 각도로 매개 변수화된다고 가정합니다.
(를) 포함하는 임의 평면 내의 원형 경로가 각도로 매개 변수화된다고 가정합니다. 
















 부분군이다.
부분군이다.








