이미지 충전 방법

영상전하법(이미지의 방법과 거울전하법으로도 알려져 있다)은 전기공학에서 기본적인 문제해결 툴이다.명칭은 문제의 경계 조건을 복제하는 상상의 전하(Dirichlet 경계 조건 또는 Neuman 경계 조건 참조)로 원래 레이아웃의 특정 요소를 대체한 것에서 유래한다.

영상 전하 방법의 유효성은 고유성 정리의 한 관점에 달려 있는데, 이 관점에 따르면 영역 전체의 전하 밀도와 모든 경계에서의 전위값이 모두 명시된 경우 볼륨 V의 전위가 고유하게 결정된다고 한다.또는, 이 코롤리를 가우스 법칙의 차등 형태에 적용하면 도체에 둘러싸이고 지정된 전하 밀도 ρ을 포함하는 V 부피에서 각 도체에 대한 총 전하가 주어지는 경우 전기장이 고유하게 결정된다는 것을 알 수 있다.전위 또는 전기장과 그에 상응하는 경계 조건에 대한 지식을 보유하면 관심 영역에서 포아송의 방정식을 만족하고 경계에서 정확한 값을 가정하는 한 분석하기 쉬운 구성을 가진 것으로 우리가 고려하고 있는 전하 분포를 교환할 수 있다.^[1]

전도면의 반사

포인트 요금

이미지 전하 방법의 가장 간단한 예로는 무한대 접지(즉, ${\displaystyle \mathrm{다음}}$과 같은 경우) 위의${\displaystyle }$(${\displaystyle 0,}$ 0${\displaystyle }$,${\displaystyle }$) ${\디스플레이$ 스타일 $(0,0,a)}$에 있는 충전 q의 점 전하를 들 수 있다.${\displaystyle \mathrm{Xy}}$ ${\displaystyle \mathrm{평면}}$의$$V${\displaystyle }$= 0 {\$displaystyle$ V$=0$ 전도성 플레이트.이 문제를 단순화하기 위해 등전위의 판을${\displaystyle }$(${\displaystyle 0,}$ ${\displaystyle 0,}$ ${\displaystyle 0}$,${\displaystyle }$-${\displaystyle }$) ${\displaystyle (0,0,-a)}$에 위치한 충전 -q로 교체할 수 있다$.$ 배열은 > 0 ${\displaystyle z>0}($즉, 전도판 위)의 어느 지점에서나 동일한 전기장을 생성하며, 플레이트를 따라 있는 전위가 0이어야 하는 경계 조건을 만족시킨다.이 상황은 원래 설정과 동등하며, 따라서 실제 전하에서의 힘은 이제 두 점 전하 사이의 쿨롱의 법칙으로 계산할 수 있다.^[2]

z축의 +a에서 +a에서 +q, -a에서 -q의 이 두 점 전하로 인해 공간의 어느 지점에서나 발생할 수 있는 전위는 다음과 같이 원통형 좌표로 주어진다.

${\displaystyle V\left(\rho ,\varphi ,z\right)={\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {q}{\sqrt {\rho ^{2}+\left(z-a\right)^{2}}}}+{\frac {-q}{\sqrt {\rho ^{2}+\left(z+a\right)^{2}}}}\right)\,}$

따라서 접지면의 표면 전하 밀도는 다음과 같다.

$\displaystyle \sigma =-\barepsilon _{0}\왼쪽.{\frac {\partial V}{\partial z}\right _{z=0}={\frac {-qa}{2\pi \reft(\rho ^{2}+a^{2}){2}\오른쪽)^{3/2}}$

또한 전도 평면에 유도된 총 전하량은 전체 평면에 걸친 전하 밀도의 적분이 될 것이므로, 다음과 같다.

${\displaystyle {\reasoned}Q_{t}&=\int _{0}^{2\pi }\int _{0}^{\infty }\sigma \left(\rho \right)\,\rho \,d\rho \,d\theta \\[6pt]&={\frac {-qa}{2\pi }}\int _{0}^{2\pi }d\theta \int _{0}^{\infty }{\frac {\rho \,d\rho }{\left(\rho ^{2}+a^{2}\오른쪽)^{3/2}}\\[6pt]&=-q\end{arged}}}$

비행기에서 유도된 총 충전량은 단순히 -q인 것으로 밝혀졌다.이는 또한 먼 거리의 입방체에서 쌍극자장이 감소하고, 따라서 무한히 큰 구체는 사라지지만 그장의 총유속은 감소한다는 점을 고려하면 가우스의 법칙에서도 알 수 있다.

전기장이 중첩 원리를 만족하기 때문에 복수 점 전하 아래의 전도면은 다른 수정 없이 각 전하 각각의 거울 영상으로 교체할 수 있다.

전기 쌍극자 모멘트

xy 면의 무한 접지 전도면 위에 ${\displaystyle \mathrm{있는}}$${\displaystyle }$(${\displaystyle 0,}$ ${\displaystyle 0}$ ,${\displaystyle }$) ${\displaystyle (0,$$0,a$$)}$에서 전기 쌍극자 모멘트 p의 이미지는 ($0,$0,a$)$에 의해 방위각으로 회전된 동일한 크기와 방향을 가진$$$쌍극자$ 모멘트다$.$That is, a dipole moment with Cartesian components ${\displaystyle (p\sin \theta \cos \phi ,p\sin \theta \sin \phi ,p\cos \theta )}$ will have in image dipole moment ${\displaystyle (-p\sin \theta \cos \phi ,-p\sin \theta \si$$n$$\phi,p\cos \theta )}$쌍극자는 다음과 같이 z 방향으로 힘을 경험한다.

${\displaystyle F=-{\frac {1}{4\pi \varepsilon_{0}{0}{3p^{2}}:{16a^{4}}}\좌측(1+\cos ^{2}\tea \right)}}$

그리고 이중극 및 전도면에 수직인 평면의 토크,

${\displaystyle \tau =-{\frac {1}{4\pi \varepsilon_{0}{0}{\frac {p^{2}}{16a^{3}}\sin 2\theta }}}$

유전 평면 인터페이스의 반사

이 구간은 확장이 필요하다.추가하면 도움이 된다. (2013년 9월)

전도면과 유사하게, 두 개의 서로 다른 유전체 매체 사이의 평면 인터페이스의 경우를 고려할 수 있다.점 전하 $q{\displaystyle }$ ${\displaystyle q}$이(가) 유전 상수 $ϵ{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$}을 가진 유전체 $ϵ{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$ 유전체와의 인터페이스는 바운드 양극화 전하를 발생시킨다$.$입자가 포함된 유전체 내부의 결과 전기장은 다른 유전체 내부의 영상 전하로 설명할 수 있는 방식으로 수정된다는 것을 알 수 있다.그러나 다른 유전체 내부에서는 영상 전하가 존재하지 않는다.^[3]

Unlike the case of the metal, the image charge ${\displaystyle q'}$ is not exactly opposite to the real charge: ${\textstyle q'={\frac {\varepsilon _{1}-\varepsilon _{2}}{\varepsilon _{1}+\varepsilon _{2}}}q}$. It may even have the same sign, if the charge is placed inside the더 강한 유전 물질(하위 유전 상수의 영역에서 제거됨).이것은 공식에서 알 수 있다.

전도구 반사

포인트 요금

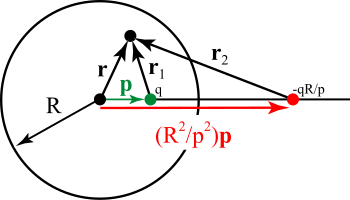
영상의 방법은 구에도 적용될 수 있다.^[4]실제로 평면에서의 영상충전의 경우는 구체의 영상충전의 특수한 경우다.그림을 참조하여, p ${\$반대의 경우, 구 외부의 전하로 인한 구 외부의 전위에는 유사한 방법으로 방법이 적용됨) $위치$에서 구 내부의 점 전하 때문에, 원점을 중심으로 한 R 반경의 접지된 구체 안에서 전위를 찾기를 바란다.$$그림에서 이것은 녹색 점으로 표현된다.q가 이 점을 책임지게 하자.접지된 구체에 대한 이 전하 이미지는 빨간색으로 표시된다.It has a charge of q′=−qR/p and lies on a line connecting the center of the sphere and the inner charge at vector position ${\displaystyle \left(R^{2}/p^{2}\right)\mathbf {p} }$. It can be seen that the potential at a point specified by radius vector ${\displaystyle \mathbf {r} }$ due to both charges단지 잠재력의 합에 의해 주어진다:

${\displaystyle 4\pi \varepsilon _{0}V(\mathbf {r} )={\frac {q}{ \mathbf {r} _{1} }}+{\frac {(-qR/p)}{ \mathbf {r} _{2} }}={\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}+{\frac {(-qR/p)}{\sqrt {r^{2}+{\frac {R^{4}}{p^{2}}}-{\frac {2R^{2}}{p^{2}}}\mathbf {r} \cdot \mathbf {p} }}}}$

가장 오른쪽 식에 곱하기:

${\displaystyle V(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\left[{\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}-{\frac {q}{\sqrt {{\frac {r^{2}p^{2}}{R^{2}}}+R^{2}-2\mathbf {r} \cdot \mathbf {p} }}}\right]}$

그리고 구의 표면(즉, r=R)에서 전위가 사라지는 것을 볼 수 있다.따라서 구체 내부의 잠재력은 두 전하의 잠재력에 대한 위의 표현에 의해 주어진다.영상 전하가 실제로 존재하지 않기 때문에 이 전위는 구 밖에서는 유효하지 않을 $것$이며, 오히려 p ${\$에서 구에 유도된 표면 전하 밀도에 대해 "입력"할 것이다$.$ 접지된 구 외부의 전위는 전하 분산에 의해서만 결정될 것이다.구를 구상하고 구 내부의 전하 분포로부터 독립할 것이다.단순성을 위해(일반성을 상실하지 않고) 내부 전하가 z축에 있다고 가정할 경우, 유도 전하 밀도는 단순히 극각 θ의 함수일 뿐이며 다음과 같이 주어진다.

$\displaystyle \sigma(\theta )=\var렙실론 _{0}\왼쪽.{\frac {\partial r}{\partial r}\오른쪽 _{R=R}={\frac {-q\왼쪽(R^{2}-p^{2}\오른쪽){4\pi R\왼쪽(R^{2}+p^{2}-2pR\cos \cos \ta \right}{3/2}}:$

구체의 총 전하량은 모든 각도에 걸쳐 통합함으로써 찾을 수 있다.

${\displaystyle Q_{t}=\int _{0}^{}\pi }d\theta \int_{0}^{2\pi }d\phi \,\\sigma (\teta )R^{2}\sin \teta =-q}$

호혜적 문제도 이 방법으로 해결된다는 점에 유의한다.만일 우리가 R 반경의 접지된 구역을 벗어나$$ 벡터 $위치{\displaystyle \mathbf{}}$ p ${\$에 전하 q를 가지고 있다면, 구 외부의 전위는 전하의 전위와 구 내부의 이미지 전하의 합에 의해 주어진다.첫 번째 경우와 마찬가지로 영상 전하도 -qR/p가 있고 벡터 ${\displaystyle 위치\mathbf{}}({\displaystyle R{}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$/ ${\displaystyle {p\mathrm{}}^{}}$ ${\displaystyle 2{}^{}}$) p ${\$에 위치하게 된다$.$ 구체 내부의 전위는 구 내부의 실제 전하 분포에만 의존하게 된다.첫 번째 경우와 달리 적분은 -qR/p 값이 될 것이다.

전기 쌍극자 모멘트

전기점 쌍극자의 이미지는 좀 더 복잡하다.만일 쌍극이 작은 거리로 분리된 두 개의 큰 전하를 나타낸다면 쌍극의 이미지는 위의 절차에 의해 전하가 수정될 뿐만 아니라 그들 사이의 거리도 수정될 것이다.Following the above procedure, it is found that a dipole with dipole moment ${\displaystyle M}$ at vector position ${\displaystyle \mathbf {p} }$ lying inside the sphere of radius R will have an image located at vector position ${\displaystyle \left(R^{2}/p^{2}\right)\mathbf {p} }$ (i.e. the단순 충전과 동일) 및 단순 충전:

${\displaystyle q'={\frac {R\mathbf {p} \cdot \mathbf {M}{p^{3}}}}}}}}}}}}:$

다음 중 쌍극자 모멘트:

${\displaystyle \mathbf {M}'=\좌측({\frac {R}{p}\우측)^{3}\좌측[-\\\mathbf {M} +{\frac {2\mathbf {p}(\mathbf {p}\cdot \mathbf {M}{2}}\우측)}}}}}}}}$

반전법

구체에 대한 영상 방법은 바로 반전법으로 이어진다.^[5]위치 $\phi {\displaystyle \mathrm{}(r,}$ ${\displaystyle \theta ,\varphi }$ )의 조화 함수를 가지고 있다면$,$ 여기서 $r{\displaystyle ,}$ ${\displaystyle \theta }$$,$${\displaystyle }$,, ${\displaystyle \varphi }$, ϕ,$$ϕ, $displaystyle r,\theta ,\phi }$은 위치의 구형 좌표인 $\displaystyle$ r, \, \, \의 위치 \disaphy가 될 것이다.

${\displaystyle \Phi '(r,\theta,\phi )={\frac {R}{r}}\Phi \left({\frac {R^{2}}:{r},\theta,\phi \right)}$

If the potential ${\displaystyle \Phi }$ arises from a set of charges of magnitude ${\displaystyle q_{i}}$ at positions ${\displaystyle (r_{i},\theta _{i},\phi _{i})}$, then the image potential will be the result of a series of charges of magnitude ${\displaystyl$$e Rq_{i}/r_{i}}$ at positions ${\displaystyle (R^{2}/r_{i},\theta _{i},\phi _{i})}$. It follows that if the potential ${\displaystyle \Phi }$ arises from a charge density ${\displaystyle \rho (r,\theta ,\phi )}$, then the image potential will be the result of a charge밀도 $\rho {\displaystyle {}^{}(r,}$ ${\displaystyle \theta }$,${\displaystyle \varphi }$ )${\displaystyle }$=${\displaystyle }$( ${\displaystyle R}$/ r${\displaystyle {}^{}}$) ${\displaystyle {5\mathrm{}}^{}}$ ${\displaystyle {}^{}}$(${\displaystyle {R\mathrm{}}^{}}$ /${\displaystyle {}^{}}$r ,${\displaystyle \theta }$, ${\displaystyle \varphi }$) ${\displaystyle \rho '(r,\theta ,\phi )=(R/r)^{5}\rho (R^{2}/r,\ta,\pi$ $)\}\}.$

참고 항목

• 켈빈 변환
• 쿨롱의 법칙
• 발산정리
• 플럭스
• 가우스 표면
• 슈바르츠 반사 원리
• 포아송 방정식의 고유성 정리
• 이미지 안테나
• 표면등가원리

참조

• Jackson, John D. (1962). Classical Electrodynamics. John Wiley & Sons.
• Jeans, James H. (1908). The Mathematical Theory of Electricity and Magnetism. Cambridge University Press.

추가 읽기

• Feynman, Richard; Leighton, Robert B.; Sands, Matthew (1989). Feynman Lectures on Physics, Mainly Electromagnetism and Matter. Addison-Wesley. ISBN 0-201-51003-0.
• Landau, Lev D.; Lifshitz, Evgeny M.; Pitaevskii, Lev P. (1960). Electrodynamics of Continuous Media 2nd Edition. London: Elsevier. ISBN 978-0-7506-2634-7.
• Purcell, Edward M. Berkeley Physics Course, Vol-2: Electricity and Magnetism (2nd ed.). McGraw-Hill.