중간 제곱법
Middle-square method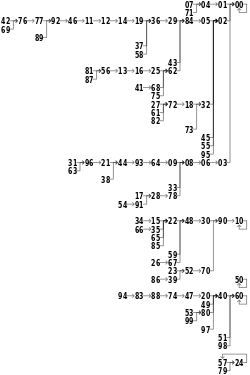
수학에서 중간 제곱법은 가성수를 생성하는 방법이다. 실제로는 그것은 좋은 방법이 아니다. 왜냐하면 그것의 기간은 보통 매우 짧고 몇몇 심각한 약점을 가지고 있기 때문이다; 충분히 반복해서, 중간 제곱법은 같은 숫자를 반복적으로 생성하기 시작하거나 시퀀스에서 이전 숫자에 대한 순환을 무한정 반복할 것이다.
역사
수학에서는
이 방법은 존 폰 노이만(John von Neumann)에 의해 발명되었고, 1949년 회의에서 설명되었다.[1]
본 노이만은 1949년 강연에서 "산술적으로 난수를 산출하는 방법을 고려하는 사람은 당연히 죄악의 상태에 있다"고 잘라 말했다. 그가 정교하게 설명한 것은 진정한 '난수'는 없고, 그저 생산하기 위한 수단일 뿐이며, '엄격한 산술 절차'는 중간 제곱법처럼 '그런 방법이 아니다'는 것이었다. 그럼에도 불구하고, 그는 이러한 방법들이 그의 ENIAC 작업에 실질적인 중요성이 있는 펀치 카드에서 "진정한" 무작위 숫자를 읽는 것보다 수백 배나 더 빠르다는 것을 발견했다. 그는 중간 사각형 시퀀스의 "파괴"가 그들에게 유리한 요인이 된다는 것을 발견했다. 왜냐하면 그것은 쉽게 감지될 수 있기 때문이다: "항상 감지되지 않은 짧은 사이클의 출현을 두려워한다."[1] 니콜라스 메트로폴리스가 '중간 제곱' 방식으로 38비트 숫자를 사용하는 방법으로 '파괴' 전 75만자리 시퀀스를 보고했다.[2]
"이바르 에클랜드의 깨진 주사위"라는 책은 이 방법이 1240년에서 1250년 사이에 에드빈 형제라고만 알려진 프란치스코 연방 수사관에 의해 어떻게 발명되었는지에 대한 자세한 설명을 제공한다.[3] 아마도, 원고는 현재 분실된 것으로 추정되지만, 호르헤 루이스 보르헤스는 에클랜드에게 바티칸 도서관에서 그가 만든 복사본을 보냈다.
Weyl 시퀀스로 중간 제곱 알고리즘을 수정하면 주기와 랜덤성이 개선된다.[4] [5]
방법
n자리 가성수 순서를 생성하려면 n자리 시작값이 생성되고 제곱되어 2n자리 숫자가 생성된다. 결과가 2n자릿수 미만일 경우 선행 0이 추가되어 보상이 이루어진다. 결과의 중간 n자리는 시퀀스에서 다음 숫자가 되고 그 결과로 반환된다. 이 과정은 더 많은 숫자를 생성하기 위해 반복된다.
n의 값은 방법이 작동하려면 짝수여야 한다. n의 값이 홀수인 경우, 선택할 수 있는 고유하게 정의된 "중간 n자릿수"가 반드시 존재할 필요는 없다. 다음을 고려하십시오. 3자리 숫자를 제곱하면 6자리 숫자(예: 5402 = 291600)를 산출할 수 있다. 중간 3자리의 경우, 6 - 3 = 3자리의 중간을 왼쪽과 오른쪽으로 분배한다. 이 숫자들을 중간 숫자의 양쪽에 균등하게 분포시키는 것은 불가능하며, 따라서 "중간 숫자"가 없다. 짝수 가치의 n자리 숫자(예: 540 → 0540)를 만들기 위해 씨앗을 왼쪽으로 패딩하는 것이 허용된다.
n자리 숫자로 된 발전기의 경우, 기간은n 8을 초과할 수 없다. 중간 n자릿수가 모두 0이면 발전기는 0을 영원히 출력한다. 만약 순서에서 숫자의 전반부가 0이면, 그 이후의 숫자는 0으로 감소할 것이다. 이러한 영점 주행은 탐지가 쉽지만, 이 방법이 실용적이기에는 너무 빈번하게 발생한다. 중간 제곱법도 0이 아닌 숫자에 걸릴 수 있다. n = 4의 경우 이 값은 0100, 2500, 3792 및 7600으로 나타난다. 다른 시드 값은 0540 → 2916 → 5030 → 3009와 같이 매우 짧은 반복 주기를 형성한다. 이러한 현상은 n = 2일 때 더욱 뚜렷하게 나타난다. 가능한 100개의 씨앗 중 어떤 것도 0, 10, 50, 60 또는 24파운드 57루프로 되돌리지 않고 14회 이상 반복을 생성하지 않기 때문이다.
구현 예
여기서 알고리즘은 Python 3에서 렌더링된다.
seed_number = 인트로(입력하다("네 자리 숫자를 입력하십시오.\n[####] ")) 번호를 붙이다 = seed_number 이미 본 = 세트() 반격하다 = 0 하는 동안에 번호를 붙이다 아닌 에 이미 본: 반격하다 += 1 이미 본.덧셈을(번호를 붙이다) 번호를 붙이다 = 인트로(발을 동동 구르다(번호를 붙이다 * 번호를 붙이다).채우다(8)[2:6]) # zfill 0의 패딩 추가 인쇄하다(f"#{반격하다}: {번호를 붙이다}") 인쇄하다(f"우리부터 시작했다. {seed_number} 그리고" f" 하고 되풀이했다. {반격하다} 단계" f와 함께 {번호를 붙이다}.") 참조
- ^ a b 1949년 논문은 1951년까지 재인쇄되지 않았다. John von Neumann, “Various techniques used in connection with random digits”, in A. S. Householder, G. E. Forsythe, and H. H. Germond, eds., Monte Carlo Method, National Bureau of Standards Applied Mathematics Series, vol. 12 (Washington, D.C.: U.S. Government Printing Office, 1951): pp. 36–38.
- ^ 도널드 크누스, 컴퓨터 프로그래밍의 기술, 제2권, 세미머셜 알고리즘, 제2권 (리딩, 매스.: 애디슨-웨슬리, 1981), 3장, 3.1절.
- ^ Ivar Ekeland (15 June 1996). The Broken Dice, and Other Mathematical Tales of Chance. University of Chicago Press. ISBN 978-0-226-19992-4.
- ^ Kneusel, Ron (2018). Random Numbers and Computers (1 ed.). Springer. pp. 13–14.
- ^ Widynski, Bernard (April 2017). "Middle Square Weyl Sequence RNG". arXiv:1704.00358.



