포크 상태

양자역학에서 Fock 상태 또는 숫자 상태는 입자 수(또는 퀀타)가 잘 정의된 Fock 공간의 요소인 양자 상태를 말한다. 이 주들은 소련의 물리학자 블라디미르 포크의 이름을 따서 명명되었다. 포크 상태는 양자역학의 두 번째 양자화 공식화에 중요한 역할을 한다.

입자 표현은 처음에 보손의 경우 폴 디락, 페르미온의 경우 파스쿠알 요르단과 유진 위그너가 자세히 다루었다.^[1]^{: 35} Fock state of bosons and fermions는 Fock 우주 생성 및 소멸 연산자와 관련하여 유용한 관계를 준수한다.

정의

하나는 N 단입자 상태의 텐서 생산물의 합으로 상태를 작성함으로써 N 비간격 동일 입자의 다중문자 상태를 명시한다. 또한, 입자의 스핀의 통합성에 따라 텐서 제품은 기초적인 단분자 Hilbert 공간의 교대(대칭) 또는 대칭 생성물이어야 한다. 구체적으로:

페르미온들은 반정수의 스핀을 가지고 있고 Pauli 배제 원칙을 준수하는 대칭 텐서 제품에 해당한다.
보손은 정수 스핀(배제 원리에 의해 관리되지 않음)을 보유하는 대칭 텐서 제품에 해당한다.

입자 수가 가변적일 경우 각 입자 번호에 대한 텐서 제품 Hilbert 공간의 직접 합으로 Fock 공간을 구성한다. Fock 공간에서는 가능한 각 원입자 상태의 입자 수를 지정함으로써 새로운 표기법인 점유번호 표기법으로 동일한 상태를 지정할 수 있다.

${\textstyle \left\{\mathbf {k} _{i}\right\}_{i\in I}}$ ${\textstyle \left\{\mathbf {k} _{i}\right\}_{i\in I}}$ ${\textstyle \left\{\mathbf {k} _{i}\right\}_{i\in I}}$ ${\textstyle \left\{\mathbf {k} _{i}\right\}_{i\in I}}$ I ${\$ 을(를) 기본 단일 입자 힐버트 공간에 있는 상태의 정형화된 기초가 되게 ${\textstyle \left\{\mathbf {k} _{i}\right\}_{i\in I}}$ 하라. 이것은 "점거수 기준"이라고 불리는 Fock 공간의 상응하는 기초를 유도한다. Fock 공간의 양자 상태는 점유 번호 기준의 요소인 경우 Fock 상태라고 불린다.

Fock 상태는 중요한 기준을 만족한다: 각 i에 대해 상태는 i번째 초등 상태 k에_i 해당하는 ${\widehat {N_{{\mathbf {k} }_{i}}}}$ 입자 번호 ${\widehat {N_{{\mathbf {k} }_{i}}}}$ N ${\widehat {N_{{\mathbf {k} }_{i}}}}$ i ^ {\displaystyle ${\widehat{N_{\mathbf {k}{}}{i}}}}}}}}$ 의 고유 상태. 해당 고유값은 해당 상태의 입자 수를 제공한다. 이 기준은 Fock 상태를 거의 정의한다(추가적으로 위상 인자를 선택해야 한다).

주어진 Fock 상태는 n $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},..n_{{\mathbf {k} }_{i}}...\rangle$ $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},..n_{{\mathbf {k} }_{i}}...\rangle$ , $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},..n_{{\mathbf {k} }_{i}}...\rangle$ $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},..n_{{\mathbf {k} }_{i}}...\rangle$ $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},..n_{{\mathbf {k} }_{i}}...\rangle$ , $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},..n_{{\mathbf {k} }_{i}}...\rangle$ . . . . . . . . . . . $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},..n_{{\mathbf {k} }_{i}}...\rangle$ ${\displaystyle n_{\mathbf {k}{{1},n_{\$ mathbf {k}{}}}{\ $mathbf{k}}}}{\$ mathbf ${}}}}}{$ 2}}로 표시된다 $.$ $n_{{\mathbf {k} }_{i}}...$ $\rangle }$ . In this expression, $n_{{\mathbf {k} }_{i}}$ denotes the number of particles in the i-th state k_i, and the particle number operator for the i-th state, ${\widehat {N_{{\mathbf {k} }_{i}}}}$ , acts on the Fock state in the following way:

{\displaystyle{\widehat{N_{{\mathbf{k}}{{i}}}n_{1},n_{\mathbf{k}_{2}}, .n_{{\mathbf {k} }_{i}}...\rangle =n_{\mathbf {k}{}}{i}n_{{\mathbf {k}{1}{1},n_{\mathbf{k}}{2}},..n_{{\mathbf {k} }_{i}}...\rangele }

따라서 Fock 상태는 고유값 $n_{{\mathbf {k} }_{i}}$ $n_{{\mathbf {k} }_{i}}$ $n_{{\mathbf {k} }_{i}}$ ${\$ 을(를) 가진 숫자 연산자의 고유 상태 입니다 $n_{{\mathbf {k} }_{i}}$ ^[2]^{: 478}

포크 상태는 종종 포크 공간의 가장 편리한 기초를 형성한다. 입자 번호가 다른 상태(따라서 번호 연산자의 고유값이 아님)의 합성인 Fock 공간의 요소는 Fock 상태가 아니다. 이러한 이유로, Fock 공간의 모든 요소를 "Fock 상태"라고 부르는 것은 아니다.

집계 입자 번호 연산자 ${\textstyle {\widehat {N}}}$ ${\textstyle {\widehat {N}}}$ ${\$ 을(를) 다음과 ${\textstyle {\widehat {N}}}$ 같이 정의하는 경우

{\widehat{N}=\sum _{i}{\widehat {N_{{\mathbf{k}}}}},

Fock 상태의 정의는 측정 $\operatorname {Var} \left({\widehat {N}}\right)=0$ $\operatorname {Var} \left({\widehat {N}}\right)=0$ ( $\operatorname {Var} \left({\widehat {N}}\right)=0$ $\operatorname {Var} \left({\widehat {N}}\right)=0$ ) $\operatorname {Var} \left({\widehat {N}}\right)=0$ = $\operatorname {Var} \left({\widehat {N}}\right)=0$ ${\displaystyle \operatorname {Var} \left({\widehat{N}\right)=0$ 즉 Fock 상태의 입자 수를 측정하면 항상 변동 없이 한정된 값을 반환한다는 것을 보장한다.

두 개의 입자를 사용하는 예제

For any final state $f\rangle$ , any Fock state of two identical particles given by $1_{\mathbf {k} _{1}},1_{\mathbf {k} _{2}}\rangle$ , and any operator ${\widehat {\mathbb {O} }}$ , we have the following condition for ind등가성:^[3]^{: 191}

{\displaystyle \left \left\langle f\left {\widehat {\mathbb {O} }}\right 1_{\mathbf {k} _{1}},1_{\mathbf {k} _{2}}\right\rangle \right ^{2}=\left \left\langle f\left {\widehat {\mathbb {O} }}\ri

ght 1_{\mathbf{k} _{2}},1_{\mathbf {k} _{1}\rigle \rigle

\rigle

\rigle

\{

2

So, we must have ${\displaystyle \left\langle f\left {\widehat {\mathbb {O} }}\right 1_{\mathbf {k} _{1}},1_{\mathbf {k} _{2}}\right\rangle =e^{i\delta }\left\langle f\left {\widehat {\mathbb {O} }}\right 1_{\$ $mathbf {k} _{2}},1_{\mathbf {k} _{1}\right\rangele }$

$e^{i\delta }=+1$ 서 $e^{i\delta }=+1$ $e^{i\delta }=+1$ $e^{i\delta }=+1$ = $e^{i\delta }=+1$ + 1 ${\displaystyle e^{i\limit }=+1},$ - $-1$ ${\displaystyle -1}($ 보손의 경우 $e^{i\delta }=+1$ $-1$ ) $\langle f|$ $\langle f|$ $displaystyle \langlef }$ 과 $\langle f|$ (와) ${\widehat {\mathbb {O} }}$ ${\$ 은(는) 임의적이기 ${\widehat {\mathbb {O} }}$ 때문에 우리는 이렇게 말할 수 있다.

\left 1_{\mathbf {k} _{1}},1_{\mathbf {k} _{2}}\right\rangle =+\left 1_{\mathbf {k} _{2}},1_{\mathbf {k} _{1}}\right\rangle

for bosons and

\left 1_{\mathbf {k} _{1}},1_{\mathbf {k} _{2}}\right\rangle =-\left 1_{\mathbf {k} _{2}},1_{\mathbf {k} _{1}}\right\rangle

for fermions.^[3]^{: 191}

숫자 연산자는 보손과 페르미온을 구별하지 않는다는 점에 유의하십시오. 실제로, 그것은 입자의 대칭 유형을 고려하지 않고 입자를 계수할 뿐이다. 그들 사이의 어떤 차이점이라도 인지하려면, 우리는 다른 연산자, 즉 생성과 소멸 연산자가 필요하다.

보소닉 포크 상태

정수 스핀이 있는 입자인 보손은 단순한 규칙을 따른다. 보손의 복합 고유 상태는 교환 운영자에 의해 작동 중 대칭이다^[4]. 예를 들어, 텐서 제품 표현에서 ${\hat {P}}\left|x_{1},x_{2}\right\rangle =\left|x_{2},x_{1}\right\rangle$ ^ x 1, ${\hat {P}}\left|x_{1},x_{2}\right\rangle =\left|x_{2},x_{1}\right\rangle$ ${\hat {P}}\left|x_{1},x_{2}\right\rangle =\left|x_{2},x_{1}\right\rangle$ ${\hat {P}}\left|x_{1},x_{2}\right\rangle =\left|x_{2},x_{1}\right\rangle$ = x 2 , ${\hat {P}}\left|x_{1},x_{2}\right\rangle =\left|x_{2},x_{1}\right\rangle$ 1 ${\hat {P}}\left|x_{1},x_{2}\right\rangle =\left|x_{2},x_{1}\right\rangle$ ${\hat {P}}\left|x_{1},x_{2}\right\rangle =\left|x_{2},x_{1}\right\rangle$ $displaystyle {\hat{P}\왼쪽 x_{1},x_{2$ }\ $rigle$ =\ $왼쪽 x_{2}, 오른쪽$ x_ ${1$ }, $오른쪽\rangele }$ 이 있다. ${\hat {P}}\left|x_{1},x_{2}\right\rangle =\left|x_{2},x_{1}\right\rangle$

보손 생성 및 소멸 연산자

우리는 이 새로운 Fock 공간 표현에서 동일한 대칭 속성을 표현할 수 있을 것이다. 이를 위해 우리는 각각 $b$ $b^{\dagger }$ $b^{\dagger }$ ${\$ b $^{\dager$ }과 $b^{\dagger }$ $b$ $b$ 로 표시된 비 Hermitian bosonic 생성 및 소멸 연산자를 소개한다.^[4] Fock 상태에서 이러한 연산자의 작용은 다음 두 방정식에 의해 주어진다.

생성 연산자 ${\textstyle b_{{\mathbf {k} }_{l}}^{\dagger }}$ ${\textstyle b_{{\mathbf {k} }_{l}}^{\dagger }}$ $†{\$ }^{\ $dager$ :
$b_{\mathbf {k}{{l}}^{}}{{{\mathbf {k}{1}{1},n_{\mathbf {k}{2}},n_{\mathbf {k}{}}}}}{{}}}}}}}}}}}}{3}}}}}}}}}}}}}}}...n_{{\mathbf {k} }_{l},...\rangele ={\sqrt{n_{{\mathbf{k}}{{l}+1}n_{1}{{{}}{{1},n_{\mathbf{k}}{2}},n_{\mathbf {k}{}}}}{}}}}}}}}}}}{{3}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}...n_{{\mathbf {k} }_{l}+1,...\rangele$ ^[4]
전멸 연산자 ${\textstyle b_{{\mathbf {k} }_{l}}}$ k ${\textstyle b_{{\mathbf {k} }_{l}}}$ ${\$ :
$b_{\mathbf {k}{}_{l}n_{1},n_{\mathbf {k}{1},{n_{2}},n_{\mathbf {k}{}}}}{{\mathbf {}}}{3}}}}}}}}}...n_{{\mathbf {k} }_{l},...\rangle ={\sqrt{n_{{\mathbf{k}}}{{l}}n_{1}{{\mathbf{k}{1}{{1},n_{\mathbf{k}}}}{{n_{\mathbf{}}}}}}}}}}{3}}}}}}}}}}}}...n_{{\mathbf {k} }_{l}-1,...\rangele$ ^[4]

The Operation of creation and annihilation operators on Bosonic Fock states.

생성 및 소멸 연산자의 비Hermitity

보소닉 포크 주의 생성 및 소멸 연산자는 에르미트인 연산자가 아니다.^[4]

창조와 전멸 운영자가 에르미트인이 아니라는 증거.

For a Fock state, $n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}\dots n_{\mathbf {k} _{l}},\dots \rangle$ ,

{\displaystyle{\begin{정렬}\left\langle n_{\mathbf{k}_{1}},n_{\mathbf{k}_{2}},n_{\mathbf{k}_{3}}\dots(_{나는}}}\left b_{\mathbf{k}_{나는}-1,\dots \right n_{\mathbf{k}_{1}},n_{\mathbf{k}_{2}},n_{\mathbf{k}_{3}}\dots(_{나는}}\right\rangle 및 ,\dots, ={\sqrt{n_{\mathbf{k}_{나는}}}}\left\langle n_{\mathbf{k}_{1.}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}\dots n_{\mathbf {k} _{l}}-1,\dots n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}\dots n_{\mathbf {k} _{l}}-1,\dots \right\rangle \\[6pt]\left(\left\langle n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}\dots n_{\mathbf {k} _{l}},\dots \left b_{\mathbf {k} _{l}}\right n_{\mathbf {k} _{1},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}\}\mathbf {k} _{l}-1,\mathbf \rangele \right)^{*}&,=\left\langle n_{\mathbf{k}_{1}},n_{\mathbf{k}_{2}},n_{\mathbf{k}_{3}}\dots(_{나는}}}\left b_{\mathbf{k}_{나는}-1\dots ^{\dagger}\right n_{\mathbf{k}_{1}},n_{\mathbf{k}_{2}},n_{\mathbf{k}_{3}}\dots(_{나는}},\dots\right\rangle \\&, ={\sqrt{n_{\mathbf{k}_{나는}}+1}}\left\langle n_{\mathbf{k}_{1}},n_{년.mathbf{k} _{2}},n_{\mathbf {k} _{3}}\dots n_{\mathbf {k} _{l}}-1\dots n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}\dots n_{\mathbf {k} _{l}}+1\dots \right\rangle \end{aligned}}}

그러므로, 창조(절제) 운영자의 연관은 그 자체로 들어가지 않는다는 것은 분명하다. 따라서, 그들은 에르미트인 운영자가 아니다.

그러나 창조(멸종) 연산자의 조정은 소멸(창조) 연산자다.^[5]^{: 45}

운영자 ID

보소닉 시스템에서 생성 및 소멸 연산자의 정류 관계는 다음과 같다.

{\displaystyle \left[b_{i}^{\,b_{j}^{\\\\b_{j}^{}\b_{j}^{}\b_{j}^{}}}}}\displaysty \reftimes \b_{i}^{i}}}}}}}}}}}}}}}}}.

^[4]

\left[b_{i}^{}\b_{j}^{\j}}^{\}\좌측[b_{i}^{\}}^{j}^{\}}}}}}=0,

^[4]

여기서 $[\ \ ,\ \ ]$ [ , $[\ \ ,\ \ ]$ ${\displaystyle [\$ \ $,\$ \ \ $]}$ 은 $[\ \ , \ \ ]$ (는) 정류자이고 $\delta _{ij}$ $\delta _{ij}$ $\delta _{ij}$ ${\$ }은 $($ 는 $\delta_{i j}$ ) 크론커 델타다.

N 보소닉 기반 $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}},...\rangle$ n k $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}},...\rangle$ , $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}},...\rangle$ n $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}},...\rangle$ $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}},...\rangle$ , $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}},...\rangle$ $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}},...\rangle$ $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}},...\rangle$ . $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}},...\rangle$ . . . . . . $|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}},...\rangle$ ${\displaystyle n_{\mathbf$ { $k}{$ 1}{ $1},n_{\mathbf {k}{{}}}}{{{}}}},n_{\mathbf{}}}}{}}}}}}}}}}}}}}}}}{{{{{{{{3}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$ $n_{{\mathbf {k} }_{l},...$ $\rangele }$

입자수(N)	보소닉 기본 상태^[6]^{: 11}
0	$0,0,0...\rangele }$
1	$\|1,0,0...\rangle$ ${\displaystyle$ $\rangele$ $\|1,0,0...\rangle$ $\|0,1,0...\rangle$ $\|0,1,0...\rangle$ , $\|0,1,0...\rangle$ ${\displaystyle 0,1,0...$ $\rangele$ $\|0,1,0...\rangle$ $\|0,0,1...\rangle$ $\|0,0,1...\rangle$ $\|0,0,1...\rangle$ ${\displaystyle 0,0,1...$ $\rangele },...$
2	$\|2,0,0...\rangle$ ${\displaystyle$ $\rangele$ $\|2,0,0...\rangle$ $\|1,1,0...\rangle$ , $\|1,1,0...\rangle$ , $\|1,1,0...\rangle$ ${\displaystyle$ $\rangele$ $\|1,1,0...\rangle$ $\|0,2,0...\rangle$ $\|0,2,0...\rangle$ , $\|0,2,0...\rangle$ ${\displaystyle 0,2,0...$ $\rangele },...$
...	...

특정 Fock 상태에 대한 조치

진공 상태의 경우—어떤 상태에도 입자가 없는 경우— $|0_{{\mathbf {k} }_{1}},0_{{\mathbf {k} }_{2}},0_{{\mathbf {k} }_{3}}...0_{{\mathbf {k} }_{l}},...\rangle$ $|0_{{\mathbf {k} }_{1}},0_{{\mathbf {k} }_{2}},0_{{\mathbf {k} }_{3}}...0_{{\mathbf {k} }_{l}},...\rangle$ , $|0_{{\mathbf {k} }_{1}},0_{{\mathbf {k} }_{2}},0_{{\mathbf {k} }_{3}}...0_{{\mathbf {k} }_{l}},...\rangle$ $|0_{{\mathbf {k} }_{1}},0_{{\mathbf {k} }_{2}},0_{{\mathbf {k} }_{3}}...0_{{\mathbf {k} }_{l}},...\rangle$ , $|0_{{\mathbf {k} }_{1}},0_{{\mathbf {k} }_{2}},0_{{\mathbf {k} }_{3}}...0_{{\mathbf {k} }_{l}},...\rangle$ $|0_{{\mathbf {k} }_{1}},0_{{\mathbf {k} }_{2}},0_{{\mathbf {k} }_{3}}...0_{{\mathbf {k} }_{l}},...\rangle$ . $|0_{{\mathbf {k} }_{1}},0_{{\mathbf {k} }_{2}},0_{{\mathbf {k} }_{3}}...0_{{\mathbf {k} }_{l}},...\rangle$ . $|0_{{\mathbf {k} }_{1}},0_{{\mathbf {k} }_{2}},0_{{\mathbf {k} }_{3}}...0_{{\mathbf {k} }_{l}},...\rangle$ . $|0_{{\mathbf {k} }_{1}},0_{{\mathbf {k} }_{2}},0_{{\mathbf {k} }_{3}}...0_{{\mathbf {k} }_{l}},...\rangle$ . . . . . . . . $|0_{{\mathbf {k} }_{1}},0_{{\mathbf {k} }_{2}},0_{{\mathbf {k} }_{3}}...0_{{\mathbf {k} }_{l}},...\rangle$ ${\displaystyle 0_{\\mathbf {k}{{$ 1} $_{{$ 1}, $0_{{\mathbf {k}{}}}{2}},0_{\mathbf{k}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$ $0_{{\mathbf {k} }_{l},...$ $\rangele$ $|0_{{\mathbf {k} }_{1}},0_{{\mathbf {k} }_{2}},0_{{\mathbf {k} }_{3}}...0_{{\mathbf {k} }_{l}},...\rangle$ 다음이 있음:
$b_{\mathbf {k}{{l}}^{}}{{{\mathbf {k}}{1}{1}{{{1},0_{{}}}{\mathbf {k}}{{{}}}}}}}}}{{\mathbf{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}...0_{{\mathbf {k} }_{l},...\rangele = 0_{{\mathbf {k}{1}_{1},0_{\mathbf {k}{}}{2}},0_{\mathbf {k}}{3}}}}...1_{{\mathbf {k} }_{l},...\rangele$
그리고, $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ k $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ 0 $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ , $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ 0 $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ , $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ . $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ . . $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ . . . . . . $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ = 0 $b_{\mathbf {k} _{l}}|0_{\mathbf {k} _{1}},0_{\mathbf {k} _{2}},0_{\mathbf {k} _{3}}...0_{\mathbf {k} _{l}},...\rangle =0$ {\ $displaystyle b_{\mathbf {k} _{l} 0_{$ 1}{ $1},0_{\mathbf {k} _{{1},{{{{}}}},0_{\mathbf {k} _}}}}}}}}}}}}}}}},},},},},},},{3},$ {k}, {k},},},}, {}, $0_{\mathbf{k} _{l},...$ $\rangele =0}$ ^[4]. 즉 l-th 생성 연산자는 l-th 상태 k에서_l 입자를 생성하며, 진공 상태는 소멸시킬 입자가 없어 소멸 연산자의 고정점이다.
우리는 적절한 수의 생성 연산자와 함께 진공 상태에서 작동함으로써 어떠한 Fock 상태도 생성할 수 있다.
$n_{\mathbf {k} _{1},n_{\mathbf {k} _{2}}...\rangele ={\frac {\좌(b_{\mathbf {k} _{1}^{\mathbf }\우)^{n_{\mathbf{k} _{1}}{1}}{\sqrt{n_{\mathbf{k} _{1}!}}}{\frac {\왼쪽(b_{\mathbf {k} _{2}}^{\mathbf }\오른쪽)^{n_{\mathbf{k} _{2}}:{\sqrt{n_{\mathbf{k} _{2}}!}}}... 0_{\mathbf {k} _{1},0_{\mathbf {k} _{2}}, ...\rangele$
단일 모드 Fock 상태의 경우, n $|n_{\mathbf {k} }\rangle$ $|n_{\mathbf {k} }\rangle$ ${\displaystyle n_{\mathbf {k}\rangele$ $|n_{\mathbf {k} }\rangle$
$b_{\mathbf {k} }^{\dagger }|n_{\mathbf {k} }\rangle ={\sqrt {n_{\mathbf {k} }+1}}|n_{\mathbf {k} }+1\rangle$ $b_{\mathbf {k} }^{\dagger }|n_{\mathbf {k} }\rangle ={\sqrt {n_{\mathbf {k} }+1}}|n_{\mathbf {k} }+1\rangle$ n $b_{\mathbf {k} }^{\dagger }|n_{\mathbf {k} }\rangle ={\sqrt {n_{\mathbf {k} }+1}}|n_{\mathbf {k} }+1\rangle$ $b_{\mathbf {k} }^{\dagger }|n_{\mathbf {k} }\rangle ={\sqrt {n_{\mathbf {k} }+1}}|n_{\mathbf {k} }+1\rangle$ = n $b_{\mathbf {k} }^{\dagger }|n_{\mathbf {k} }\rangle ={\sqrt {n_{\mathbf {k} }+1}}|n_{\mathbf {k} }+1\rangle$ + $b_{\mathbf {k} }^{\dagger }|n_{\mathbf {k} }\rangle ={\sqrt {n_{\mathbf {k} }+1}}|n_{\mathbf {k} }+1\rangle$ $b_{\mathbf {k} }^{\dagger }|n_{\mathbf {k} }\rangle ={\sqrt {n_{\mathbf {k} }+1}}|n_{\mathbf {k} }+1\rangle$ + 1 k + $b_{\mathbf {k} }^{\dagger }|n_{\mathbf {k} }\rangle ={\sqrt {n_{\mathbf {k} }+1}}|n_{\mathbf {k} }+1\rangle$ $b_{\mathbf {k} }^{\dagger }|n_{\mathbf {k} }\rangle ={\sqrt {n_{\mathbf {k} }+1}}|n_{\mathbf {k} }+1\rangle$ {\ $displaystyle b_{\mathbf {k}^{\n_{\mathbf {k}}}\range ={\sqrt {n_{\mathbf {n}+1}n_{{{\mathb}}}+1rangle$ }, and $b_{\mathbf {k} }^{\dagger }|n_{\mathbf {k} }\rangle ={\sqrt {n_{\mathbf {k} }+1}}|n_{\mathbf {k} }+1\rangle$ }, }, }, }}, and }, and }, }, }, }, }, }.

$b_{\mathbf {k} n_{\mathbf {k}}\rangel ={\sqrt {n_{\mathbf{k}}}n_{\mathbf {k}{}}}{\mathbf {k}-1\rangele$

수 연산자의 작용

The number operators ${\textstyle {\widehat {N_{{\mathbf {k} }_{l}}}}}$ for a bosonic system are given by ${\widehat {N_{{\mathbf {k} }_{l}}}}=b_{{\mathbf {k} }_{l}}^{\dagger }b_{{\mathbf {k} }_{l}}$ , where ${\widehat {N_{{\mathbf {k} }_{l}}}}|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}}...\rangle =n_{{\mathbf {k} }_{l}}|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}}...\rangle$ ${\displaystyle {\widehat {N_{{\mathbf {k} }_{l}}}} n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...$ $n_{{\mathbf {k} }_{l}}...$ $\rangle =n_{\mathbf {k}{{}_{l}n_{1},n_{{1}{{\mathbf{k}}{{1},{n_{{}},{\mathbf{k}}}}{{}}}}}}}},{3}}}}}}}...$ $n_{{\mathbf {k} }_{l}}...$ $\rangele }$

숫자 연산자는 에르미트 연산자다.

보소닉 포크 상태의 대칭 거동

생성 및 소멸 연산자의 정류 관계는 보소닉 포크 상태가 입자 교환 하에서 적절한 대칭적 행동을 갖도록 보장한다. 여기서 두 상태(say, l, m) 사이의 입자 교환은 상태 l에서 입자를 소멸시키고 상태 m에서 입자를 생성함으로써 이루어진다. Fock 상태 $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},....n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ = n $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},....n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},....n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ , $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},....n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ n $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},....n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},....n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ , $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},....n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ . $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},....n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ . . $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},....n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ . . . . . . . . . . . . . . . . . . $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},....n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ ${\$ { $k} _{1},{1$ }, $n_{mathbf{k}}}}.$ $n_{\mathbf{k} _{l}}...$ $\right\rangle }$ , and want to shift a particle from state $k_{l}$ to state $k_{m}$ , then we operate the Fock state by $b_{\mathbf {k} _{m}}^{\dagger }b_{\mathbf {k} _{l}}$ in the following way:

Using the commutation relation we have, $b_{\mathbf {k} _{m}}^{\dagger }.b_{\mathbf {k} _{l}}=b_{\mathbf {k} _{l}}.b_{\mathbf {k} _{m}}^{\dagger }$

{\displaystyle{\mathbf {k} _{m}^{\b_{\mathbf {k} _{l}\{l}\{{1},n_{\mathbf {k} _{1}{1},n_{\mathbf {k} _{m}}}}.n_{\mathbf{k} _{l}}...\right\rangele &=b_{\mathbf {k} _{l}.b_{\mathbf {k} _{m}^{\mathbf {k}\{1}{1},n_{\mathbf {k} _{1}, ....n_{\mathbf {k} _{m}}}}}}}}}}...n_{\mathbf{k} _{l}}...\right\rangle \\&={\sqrt {n_{\mathbf {k} _{m}}+1}}{\sqrt {n_{\mathbf {k} _{l}}}}\left n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},....n_{\mathbf {k} _{m}}+1...n_{\mathbf {k} _{l}-1...\right\rangele \end{aigned}}

따라서, Bosonic Fock 상태는 Exchange 운영자에 의해 작동 중 대칭으로 동작한다.

$|0\rangle$ 함수 0 $|0\rangle$ $0\rangele$
$|1\rangle$ er {\ $displaystyle 1\rangele}$ 의 Wigner 함수
$|2\rangle$ er {\ $displaystyle 2\rangele}$ 의 Wigner 함수
$|3\rangle$ 함수 3 $|3\rangle$ $3\rangele$
$|4\rangle$ er {\ $displaystyle 4\rangele}$ 의 Wigner 함수

페르미오닉 포크 주

페르미온 생성 및 소멸 연산자

를 Fermionic 포크 우리는non-Hermitian 페르미온 창조와 소멸 operators,[4] Fermionic 포크 상태에 대해 정의된 소개할 서술하면, fermions의 역 대칭 행동을 유지할 수 있도록 하려면 ψ ⟩)nk1, nk2, nk3... nkl,... ⟩{\displaystyle \psi \rangle)n_{{\math.남자 친구 ${k} }_{1},n_{{\mathbf {k}{}}{2}},n_{{\mathbf {k}{}_{3}}}...$ $n_{{\mathbf {k} }_{l},...$ $\rangele }$ 을 $|\psi \rangle =|n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},n_{{\mathbf {k} }_{3}}...n_{{\mathbf {k} }_{l}},...\rangle$ (^[4]를) 다음과 같이 입력하십시오.

생성 연산자 $c_{{\mathbf {k} }_{l}}^{\dagger }$ $c_{{\mathbf {k} }_{l}}^{\dagger }$ $c_{{\mathbf {k} }_{l}}^{\dagger }$ $c_{{\mathbf {k} }_{l}}^{\dagger }$ ${\$ l}^{\ $dager }}}}}$ 은 $c_{{\mathbf {k} }_{l}}^{\dagger }$ (는) 다음과 같이 작용한다.
$c_{\mathbf {k}{{l}}^{}}}{{{\mathbf {k}{1}{1},n_{\mathbf {k}{2}},n_{\mathbf {k}{}}}}}{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}...n_{{\mathbf {k} }_{l},...\rangele ={\sqrt{n_{{\mathbf{k}}{{l}+1}n_{1}{{{}}{{1},n_{\mathbf{k}}{2}},n_{\mathbf {k}{}}}}{}}}}}}}}}}}{{3}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}...n_{{\mathbf {k} }_{l}+1,...\rangele$ ^[4]
소멸 연산자 ${\textstyle c_{{\mathbf {k} }_{l}}}$ ${\textstyle c_{{\mathbf {k} }_{l}}}$ ${\textstyle c_{{\mathbf {k} }_{l}}}$ ${\$ k $} }_{l}}}$ 은(는) 다음과 같이 작용한다 ${\textstyle c_{{\mathbf {k} }_{l}}}$ .
$c_{\mathbf {k}{}_{l}n_{1},n_{\mathbf {k}{1},{n_{2}},n_{\mathbf {k}{}}}}{{\mathbf {}}}{3}}}}}}}}}...n_{{\mathbf {k} }_{l},...\rangle ={\sqrt{n_{{\mathbf{k}}}{{l}}n_{1}{{\mathbf{k}{1}{{1},n_{\mathbf{k}}}}{{n_{\mathbf{}}}}}}}}}}{3}}}}}}}}}}}}...n_{{\mathbf {k} }_{l}-1,...\rangele$

이 두 가지 작용은 대칭적으로 행해지고, 나중에 논의하기로 한다.

운영자 ID

페르미온 시스템에서 생성 및 소멸 운영자의 반공관계는 다음과 같다.

{\begin{aligned}\left\{c_{i}^{\,},c_{j}^{\dagger }\right\}\equiv c_{i}^{\,}c_{j}^{\dagger }+c_{j}^{\dagger }c_{i}^{\,}&=\delta _{ij},\\\left\{c_{i}^{\dagger },c_{j}^{\dagger }\right\}=\left\{c_{i}^{\,},c_{j}^{\,}\right\}&=0,\end{aligned}}

^[4]

여기서 ${\{\ ,\ \}}$ { ${\{\ ,\ \}}$ , ${\{\ ,\ \}}$ ${\$ 은 ${\{\ ,\ \}}$ (는) 안티코무터이고 $\delta _{ij}$ $\delta _{ij}$ $\delta _{ij}$ ${\$ 은 $\delta_{i j}$ (는) 크론커 델타다. 이러한 반공관계는 페르미오닉 포크 상태의 대칭적 행동을 보여주는 데 사용될 수 있다.

수 연산자의 작용

Number operators ${\textstyle {\widehat {N_{{\mathbf {k} }_{l}}}}}$ for Fermions are given by ${\widehat {N_{{\mathbf {k} }_{l}}}}=c_{{\mathbf {k} }_{l}}^{\dagger }.c_{{\mathbf {k} }_{l}}$ .

{\widehat{N_{\mathbf{k}}}{{l}}n_{1}{{\mathbf {k}{1}{1},n_{n_{\mathbf {k}}}{{}}}}},{\mathbf{}}}}{3}}}}...n_{{\mathbf {k} }_{l},...\rangle =n_{\mathbf {k}{{}_{l}n_{1},n_{{1}{{\mathbf{k}}{{1},{n_{{}},{\mathbf{k}}}}{{}}}}}}}},{3}}}}}}}...n_{{\mathbf {k} }_{l},...\rangele

^[4]

최대직업번호

생성 및 소멸 연산자뿐만 아니라 숫자 연산자의 작용도 보소닉 연산자와 같아 보일 수 있지만, 진정한 반전은 페르미오닉 포크 상태에 있는 각 주의 최대 점령수에서 비롯된다. Extending the 2-particle fermionic example above, we first must convince ourselves that a fermionic Fock state ${\displaystyle \psi \rangle =\left n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...$ $n_{\mathbf{k} _{l}}...$ $\right\rangele }$ 은(는) 다음과 같이 고유개킷의 텐서 제품에 일정량의 순열 연산자를 적용하여 얻는다 $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf {k} _{l}}...\right\rangle$ .

\left n_{\mathbf {k} _{1},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}}}...n_{\mathbf{k} _{l}}...\rigle =S_{-}\왼쪽 i_{1},i_{2},i_{3}...i_{l}...\right\rangele ={\frac {1}{\sqrt {N!}}}{\begin{vmatrix}\left i_{1}\right\rangle _{1}&\cdots &\left i_{1}\right\rangle _{N}\\\vdots &\ddots &\vdots \\\left i_{N}\right\rangle _{1}&\cdots &\left i_{N}\right\rangle _{N}\end{vmatrix}}

^[7]^{: 16}

이 결정 인자를 슬레이터 결정 인자라고 한다.^{[citation needed]} 단일 입자 상태 중 하나가 동일한 경우 슬레이터 결정 인자의 두 행이 같으므로 결정 인자는 0이 된다. 따라서 동일한 페르미온 두 개가 동일한 상태(Pauli 제외 원리의 진술)를 차지해서는 안 된다. 따라서 단일 주의 점령 번호는 0 또는 1이다. 페르미온 Fock 상태 ${\widehat {N_{{\mathbf {k} }_{l}}}}$ k ${\widehat {N_{{\mathbf {k} }_{l}}}}$ ${\widehat {N_{{\mathbf {k} }_{l}}}}$ ${\$ 과(와) 관련된 고유값은 0 또는 1이어야 한다 ${\widehat {N_{{\mathbf {k} }_{l}}}}$ .

N fermionic basises $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf {k} _{l}},...\right\rangle$ $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf {k} _{l}},...\right\rangle$ 1, $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf {k} _{l}},...\right\rangle$ n $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf {k} _{l}},...\right\rangle$ $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf {k} _{l}},...\right\rangle$ , $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf {k} _{l}},...\right\rangle$ $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf {k} _{l}},...\right\rangle$ $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf {k} _{l}},...\right\rangle$ . $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf {k} _{l}},...\right\rangle$ . . . . . $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf {k} _{l}},...\right\rangle$ ${\$ $n_{\mathbf{k} _{l},...$ $\right\rangele }$

입자수(N)	페르미온 기초^[6]^{: 11} 주
0	$0,0,0...\rangele }$
1	$\|1,0,0...\rangle$ ${\displaystyle$ $\rangele$ $\|1,0,0...\rangle$ $\|0,1,0...\rangle$ $\|0,1,0...\rangle$ , $\|0,1,0...\rangle$ ${\displaystyle 0,1,0...$ $\rangele$ $\|0,1,0...\rangle$ $\|0,0,1...\rangle$ $\|0,0,1...\rangle$ $\|0,0,1...\rangle$ ${\displaystyle 0,0,1...$ $\rangele },...$
2	$\|1,1,0...\rangle$ ${\displaystyle$ $\rangele$ $\|1,1,0...\rangle$ $\|0,1,1...\rangle$ $\|0,1,1...\rangle$ , $\|0,1,1...\rangle$ ${\displaystyle 0,1,1...$ $\rangele$ $\|0,1,1...\rangle$ $\|0,1,0,1...\rangle$ $\|0,1,0,1...\rangle$ , $\|0,1,0,1...\rangle$ $\|0,1,0,1...\rangle$ ${\displaystyle 0,1,0,1...$ $\rangele$ $\|0,1,0,1...\rangle$ $\|1,0,1,0...\rangle$ , $\|1,0,1,0...\rangle$ $\|1,0,1,0...\rangle$ , $\|1,0,1,0...\rangle$ ${\displaystyle$ $\rangele }...$
...	...

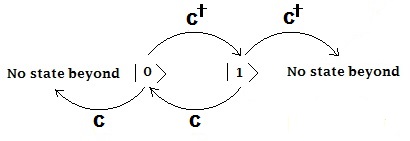
특정 Fock 상태에 대한 조치

The operation of creation and annihilation operators on Fermionic Fock states.

단일 모드 Fermionic Fock 상태의 경우 $\left|0_{\mathbf {k} }\right\rangle$ $\left|0_{\mathbf {k} }\right\rangle$ ${\$ $\left|0_{\mathbf {k} }\right\rangle$
$c_{\mathbf {k}^{}\mathbf {k}\왼쪽 0_{\mathbf {k}}\rigle =\왼쪽 1_{\mathbf {k}\right\rangele }$
및 $c_{\mathbf {k} }^{\dagger }\left|1_{\mathbf {k} }\right\rangle =0$ $c_{\mathbf {k} }^{\dagger }\left|1_{\mathbf {k} }\right\rangle =0$ 1 $c_{\mathbf {k} }^{\dagger }\left|1_{\mathbf {k} }\right\rangle =0$ = $c_{\mathbf {k} }^{\dagger }\left|1_{\mathbf {k} }\right\rangle =0$ ${\displaystyle c_{\mathbf {k}{}^{\mathbf$ {k $}\왼쪽$ 1_ ${\mathbf {k}}}\rigle =0$ 모든 주의 최대 점령 횟수는 1이므로. 파울리 배제 원칙에 명시된 바와 같이 페르미온 1개 이하가 동일한 주를 점유할 수 없다.
단일 $\left|1_{\mathbf {k} }\right\rangle$ Fermionic Fock 상태의 경우, 1k $\left|1_{\mathbf {k} }\right\rangle$ ${\$ $\left|1_{\mathbf {k} }\right\rangle$
$c_{\mathbf {k}\왼쪽 1_{\mathbf {k}}\오른쪽\rangele =\왼쪽 0_{\mathbf {k}\오른쪽\rangele$
$c_{\mathbf {k} }\left|0_{\mathbf {k} }\right\rangle =0$ $c_{\mathbf {k} }\left|0_{\mathbf {k} }\right\rangle =0$ $c_{\mathbf {k} }\left|0_{\mathbf {k} }\right\rangle =0$ $c_{\mathbf {k} }\left|0_{\mathbf {k} }\right\rangle =0$ $c_{\mathbf {k} }\left|0_{\mathbf {k} }\right\rangle =0$ = 0 $c_{\mathbf {k} }\left|0_{\mathbf {k} }\right\rangle =0$ {\ $displaystyle c_{\mathbf {k}}\왼쪽$ 0_ ${\mathbf {k}}\rigle =0$ 입자 번호는 0보다 작을 수 없으므로
멀티모드 페르미오닉 포크 상태의 경우 $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{\beta }},n_{\mathbf {k} _{\alpha }},...\right\rangle$ . $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{\beta }},n_{\mathbf {k} _{\alpha }},...\right\rangle$ k $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{\beta }},n_{\mathbf {k} _{\alpha }},...\right\rangle$ , $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{\beta }},n_{\mathbf {k} _{\alpha }},...\right\rangle$ . . . . . . . $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{\beta }},n_{\mathbf {k} _{\alpha }},...\right\rangle$ k $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{\beta }},n_{\mathbf {k} _{\alpha }},...\right\rangle$ , n $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{\beta }},n_{\mathbf {k} _{\alpha }},...\right\rangle$ $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{\beta }},n_{\mathbf {k} _{\alpha }},...\right\rangle$ , $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{\beta }},n_{\mathbf {k} _{\alpha }},...\right\rangle$ . $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{\beta }},n_{\mathbf {k} _{\alpha }},...\right\rangle$ . . . $\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{\beta }},n_{\mathbf {k} _{\alpha }},...\right\rangle$ ${\$ 1}, $n_{\mathbf {k} _{1$ },{{1 $},nmathbf$ {k $},{2$ }}...로 표현된다 $.$ $n_{\mathbf{k} _{\mathbf{k} _{\mathbf {k} _{\mathbf }}, _{\mathbf },$ $\right\rangele }$
${\displaystyle c_{\mathbf {k} _{\alpha }}\left n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...$ $n_{\mathbf{k} _{\mathbf{k} _{\mathbf {k} _{\mathbf }}, _{\mathbf },$ $\right\rangle =(-1)^{\sum _{\beta <\alpha }n_{\beta }}\left n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...,n_{\mathbf {k} _{\beta }},1-n_{\mathbf {k} _{\alpha }},...$ $\right\rangele$
여기서 $(-1)^{\sum _{\beta <\alpha }n_{\beta }}$ ( $(-1)^{\sum _{\beta <\alpha }n_{\beta }}$ - $(-1)^{\sum _{\beta <\alpha }n_{\beta }}$ ) $(-1)^{\sum _{\beta <\alpha }n_{\beta }}$ < $(-1)^{\sum _{\beta <\alpha }n_{\beta }}$ n $(-1)^{\sum _{\beta <\alpha }n_{\beta }}$ β ${\$ 은 $(-1)^{\sum _{\beta <\alpha }n_{\beta }}$ 관련 단일 입자 상태의 순서와 모든 이전 주의 페르미온 점령 번호 추가에 따라 달라지는 요르단-위너 문자열이라고 불린다.^[5]^{: 88}

페르미오닉 포크 상태의 비대칭 거동

거래소 운영자 하의 페르미온 상태의 비대칭적 행동은 반공관계에서 처리된다. 여기서 두 상태 사이의 입자 교환은 한 상태에서 한 입자를 섬멸하고 다른 상태에서 한 입자를 생성함으로써 이루어진다. Fock 상태 $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ , $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ n $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ , $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ . $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ . . . $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ . . . . . . . . . . . . . . . . . $|\psi \rangle =\left|n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},...n_{\mathbf {k} _{m}}...n_{\mathbf {k} _{l}}...\right\rangle$ ${\$ $n_{\mathbf{k} _{m}}...$ $n_{\mathbf{k} _{l}}...$ $\right\rangle }$ and want to shift a particle from state $k_{l}$ to state $k_{m}$ , then we operate the Fock state by $c_{\mathbf {k} _{m}}^{\dagger }.c_{\mathbf {k} _{l}}$ in the following way:

우리가 가진 반공관계로

c_{\mathbf {k} _{m}^{{m}}{m}^{m}^{m}{mathbf {k} _{l}=-c_{\mathbf {k}{mathbf}{m}^{\m}}}}}}}}}}}}{mathb}}}}}{\mathbf{\c}}}}}}}}}}}}}}}}}}}}}}}

c_{\mathbf{k} _{m}^{\c_{\mathbf {k} _{l}\{l}\{1},n_{\mathbf {k} _{2}}, ....n_{\mathbf{k}}}}}...n_{\mathbf{k} _{l}}...\rigle ={\sqrt{n_{\mathbf{k} _{m}+1}{{m}+1}{\sqrt{n_{l}}}}\{\mathbf {k}}{1}{1}{1},n_{mathbf{k}}}}}}{mathathbf{m+}}}}}}}}}}}}}}}}}}}}}}}}}}}}.n_{\mathbf {k} _{l}-1...\right\rangele

그렇지만

{\begin{aligned}&c_{{\mathbf {k} }_{l}}.c_{{\mathbf {k} }_{m}}^{\dagger } n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},....n_{{\mathbf {k} }_{m}}...n_{{\mathbf {k} }_{l},...\rangle \\={}-&c_{{\mathbf {k} }_{m}}^{\dagger }.c_{{\mathbf {k} }_{l}} n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},....n_{{\mathbf {k} }_{m}}...n_{{\mathbf {k} }_{l},...\rangle \\={}-&{\sqrt {n_{{\mathbf {k} }_{m}}+1}}{\sqrt {n_{{\mathbf {k} }_{l}}}} n_{{\mathbf {k} }_{1}},n_{{\mathbf {k} }_{2}},....n_{{\mathbf {k} }_{m}}+1...n_{{\mathbf {k} }_{l}-1,...\rangele \end{aigned}}

따라서 페르미온 Fock 상태는 입자 교환 연산자에 의해 작동 중인 대칭이다.

포크 상태는 일반적으로 에너지 고유 상태가 아니다.

2차 정량화 이론에서 해밀턴 밀도 함수는 다음과 같이 주어진다.

{\mathfrak{H}={\frac {1}{2m}\nabla _{i}\nabla ^{*(x)\\nabla _{i}\psi(x)

^[3]^{: 189}

총 해밀턴인은 에 의해 주어진다.

{\begin{aligned}{\mathcal {H}}&=\int d^{3}x\,{\mathfrak {H}}=\int d^{3}x\psi ^{*}(x)\left(-{\frac {\nabla ^{2}}{2m}}\right)\psi (x)\\\therefore {\mathfrak {H}}&=-{\frac {\nabla ^{2}}{2m}}\end{aligned}}

자유 슈뢰딩거 ^[3]^{: 189}이론에서

{\mathfrak {H}\psi _{n}^{{n}^{n}^{n(+)={2}}:\psi _{n}^{n}^{0}{n}^{n}{n}^{n}}{n}}^{n}}}(x)

그리고

\int d^{3}x\,\i1\{n}^{n}^{*(x)\,\i1\{n}^{n}^{n}(+)=\n'}}

그리고

\psi (x)=\sum _{n}a_{n}\psi _{n}^{(+)}(x)

(

\psi (x)=\sum _{n}a_{n}\psi _{n}^{(+)}(x)

)

\psi (x)=\sum _{n}a_{n}\psi _{n}^{(+)}(x)

=

\psi (x)=\sum _{n}a_{n}\psi _{n}^{(+)}(x)

\psi (x)=\sum _{n}a_{n}\psi _{n}^{(+)}(x)

\psi (x)=\sum _{n}a_{n}\psi _{n}^{(+)}(x)

n (

\psi (x)=\sum _{n}a_{n}\psi _{n}^{(+)}(x)

) (

\psi (x)=\sum _{n}a_{n}\psi _{n}^{(+)}(x)

)

\psi (x)=\sum _{n}a_{n}\psi _{n}^{(+)}(x)

{\

displaystyle \psi(x)=\sum _{n}a_{n}\reason _{n

}^{n

^(+)}(x

$a_{n}$ 서 n ${\$ 은 $a_{n}$ (는) 소멸 연산자다.

\therefore {\mathcal {H}}=\sum _{n,n'}\int d^{3}x\,a_{n'}^{\dagger }\psi _{n'}^{(+)^{*}}(x)\,{\mathfrak {H}}a_{n}\psi _{n}^{(+)}(x)

비접촉식 입자에 대해서만 ${\mathfrak {H}}$ ${\$ $a_{n}$ n ${\$ 통근한다 $a_{n}$ . 일반적으로 통근하지 않는다. 비 상호작용 입자의 경우,

{\mathcal {H}}=\sum _{n,n'}\int d^{3}x\,a_{n'}^{\dagger }\psi _{n'}^{(+)^{*}}(x)\,E_{n}^{0}\psi _{n}^{(+)}(x)a_{n}=\sum _{n,n'}E_{n}^{0}a_{n'}^{\dagger }a_{n}\delta _{nn'}=\sum _{n}E_{n}^{0}a_{n}^{\dagger }a_{n}=\sum _{n}E_{n}^{0}{\widehat {N}}

그들이 통근하지 않으면 해밀턴인은 위의 표현을 하지 않을 것이다. 그러므로 일반적으로 Fock 상태는 시스템의 에너지 고유 상태가 아니다.

진공변동

진공 상태 또는 $|0\rangle$ $|0\rangle$ $0\rangele$ 은 $|0\rangle$ (는) 가장 낮은 에너지의 상태 및{\ $displaystyle a}$ 및 $a$ $\$ {\ $displaystyle$ a $^{\dager}}}$ 의 $a^\dagger$ 기대 값이다.

a 0\rangele =0=\langle 0 a^{\cHB }

전기장과 자기장과 벡터 전위는 동일한 일반 형태의 모드 확장을 가진다.

F\left({\vec {r},t\오른쪽)=\varepsilon ae^{i{\bec}x-\omega t}+h\cdot c

따라서 이러한 필드 연산자의 기대값이 진공 상태에서 소멸되는 것을 쉽게 알 수 있다.

\langle 0 F 0\angle =0

그러나 이들 필드 연산자의 제곱의 기대값이 0이 아니라는 것을 알 수 있다. 따라서 현장에서는 제로 앙상블 평균에 대한 변동이 있다. 이러한 진공 변동은 양자 광학에서의 램 시프트를 포함한 많은 흥미로운 현상의 원인이 된다.

멀티 모드 포크 상태

다중 모드 필드에서 각 생성 및 소멸 연산자는 자체 모드로 작동한다. So $a_{\mathbf {k} _{l}}$ and $a_{\mathbf {k} _{l}}^{\dagger }$ will operate only on $\left n_{\mathbf {k} _{l}}\right\rangle$ . Since operators corresponding to different modes operate in different sub-spaces of the Hilbert 공간, 전체 필드는 다음 모든 모드에서 $|n_{\mathbf {k} _{l}}\rangle$ $|n_{\mathbf {k} _{l}}\rangle$ k $|n_{\mathbf {k} _{l}}\rangle$ $|n_{\mathbf {k} _{l}}\rangle$ $n_{\mathbf {k} _{l}\rangele$ 의 직접 산물이다.

\left n_{\mathbf {k} _{1}}\right\rangle \left n_{\mathbf {k} _{2}}\right\rangle \left n_{\mathbf {k} _{3}}\right\rangle \ldots \equiv \left n_{\mathbf {k} _{1}},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf{k} _{l}}...\right\rangle \equiv \왼쪽 \{n_{\mathbf {k}\}\\right\rangele

생성 및 소멸 연산자는 자체 모드의 숫자 상태만 올리거나 낮추어 멀티 모드 상태에서 작동한다.

{\displaystyle{\mathbf{k}a_{{\mathbf{k}}}{{l}n_{1},n_{\mathbf {k}{1}{{}}},n_{\mathbf {k}{}}}},{\mathbf{}}}}}{3}}...n_{{\mathbf {k} }_{l},...\rangle &={\sqrt{n_{\mathbf{k}}{{}_{l}}n_{1}{{{\mathbf {k}{1}{1},n_{\mathbf {k}}{2}},n_{\mathbf{k}}}}{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}...n_{{\mathbf {k} }_{l}-1,...\rangle \\a_{\mathbf{k}}{l}^{}}{{l}}}^{{{\mathbf {k}{1}{1},n_{\mathbf {k}}{2}},n_{\mathbf {k}{}}}}}}}}{3}}}}}}}}}}}}}}}}}}}}...n_{{\mathbf {k} }_{l},...\rangle &={\sqrt{n_{{\mathbf{k}}{{l}+1}n_{1}{{{}}{{{}},n_{\mathbf{k}}}{{2}},n_{\mathbf{k}}}{}}}}}}{3}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}...n_{{\mathbf {k} }_{l}+1,...\rangele \end{aigned}}}

또한 각 모드의 숫자 연산자의 합인 필드에 대한 총 숫자 연산자를 정의한다.

{\hat{n}_{\mathbf {k}}}=\sum {n}{\mathbf {k} _{l}}}

멀티 모드 Fock 상태는 고유값이 모든 모드의 총 점령 번호인 총 수 연산자의 고유 벡터다.

{\hat{n}_{\mathbf{k}}} \n_{\mathbf {k}\}\rangele =\ref(\sum n_{\\mathbf {k} _{l}\right) \{n_{mathbf {}\}}\rangele

비 상호작용 입자의 경우, 번호 연산자와 해밀턴이 서로 통근하므로 다중 모드 Fock 상태는 멀티 모드 해밀턴의 고유 지위가 된다.

{\hat {H}}\left \{n_{\mathbf {k} }\}\right\rangle =\left(\sum \hbar \omega \left(n_{\mathbf {k} _{l}}+{\frac {1}{2}}\right)\right)\left \{n_{\mathbf {k} }\}\right\rangle

단일 광자 상태의 소스

단일 광자는 단일 방출체(atoms, 질소 방사성 센터,^[8] Quantum dot^[9])를 사용하여 정기적으로 생성된다. 그러나 이러한 출처가 항상 매우 효율적인 것은 아니며, 실제로 단일 광자를 요구 시 얻을 확률은 낮으며, 종종 복잡하고 부적절하여 실험실 환경에서 벗어날 수 있다.

비결정론적 행동을 희생하고 이러한 문제들을 극복하는 다른 원천들이 일반적으로 사용된다. 예고된 단일 광자 선원은 쌍이 분할되는 확률론적 2광자 선원으로, 한 광자의 검출은 나머지 광자의 존재를 예고한다. 이러한 선원은 일반적으로 정기적으로 폴링된 리튬 니오베이트(후발 파라메트릭 다운-변환) 또는 실리콘(후발 4파 혼합)과 같은 일부 물질의 광학적 비선형성에 의존한다.

비분류적 행동

Fock 주들의 Gloeber-Sudarshan P 표현은 이러한 주들이 순전히 양자 역학이고 고전적인 상대도 없다는 것을 보여준다. $\scriptstyle \varphi (\alpha )\,$ ( $\scriptstyle \varphi (\alpha )\,$ ) ${\$ 의 $\scriptstyle\varphi(\alpha) \,$ ^{[clarification needed]} 이러한 상태는 Dirac 델타 함수의 $2n$ $displaystyle 2n}$ 'th번째 파생상품이므로 고전적인 확률 분포가 아니다.

참고 항목

참조

^ Friedrichs, K. O. (1953). Mathematical aspects of the Quantum Theory of Fields. Interscience Publishers. ASIN B0006ATGK4.
^ Mandel, Wolf (1995). Optical coherence and quantum optics. Cambridge University Press. ISBN 0521417112.
^ ^a ^b ^c ^d Gross, Franz (1999). Relativistic Quantum Mechanics and Field Theory. Wiley-VCH. ISBN 0471353868.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ "Quantum Mechanics 1 Lecture Notes on Identical Particles, TIFR, Mumbai" (PDF).
^ ^a ^b Altland, Alexander; Simons, Ben (2006). Condensed Matter Field Theory. Cambridge University Press. ISBN 0521769752.
^ ^a ^b Bruus, Flensberg (2003). Many-Body Quantum Theory in Condensed Matter Physics: An Introduction. OUP Oxford. ISBN 0198566336.
^ Schwabl, Hilton, Lahee (2008). Advanced Quantum Mechanics. Springer. ISBN 978-3540850618.{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크)
^ C. Kurtsiefer, S. Mayer, P. Zarda, Patrick and H. Weinfurter, (2000), "안정적인 단일 광자의 솔리드 스테이트 소스", Phys. 레트 85(2) 290--293, doi 10.1103/PhysRevRevlett.85.290
^ 산토리, M. 펠튼, G. 솔로몬, Y. 데일, Y. 야마모토(2001), "퀀텀 도트에서 단일 광자 트리거", 물리적 Rev. Let. 86 (8):1502--1505 DOI 10.1103/PhysRevRevlett.86.1502

외부 링크

MIT의 Bladan Vuletic은 Fock 상태(예: 단일 광자)를 생성하기 위해 원자 앙상블을 사용해왔다(PDF).
대화형 실험 QuantumLab으로 단일 광자 상태(Fock 상태) 생성 및 측정

[Friedrichs-1] Friedrichs, K. O. (1953). Mathematical aspects of the Quantum Theory of Fields. Interscience Publishers. ASIN B0006ATGK4.

[Mandel-2] Mandel, Wolf (1995). Optical coherence and quantum optics. Cambridge University Press. ISBN 0521417112.

[FGross-3] Gross, Franz (1999). Relativistic Quantum Mechanics and Field Theory. Wiley-VCH. ISBN 0471353868.

[TIFR-4] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ "Quantum Mechanics 1 Lecture Notes on Identical Particles, TIFR, Mumbai" (PDF).

[Altland-5] Altland, Alexander; Simons, Ben (2006). Condensed Matter Field Theory. Cambridge University Press. ISBN 0521769752.

[Bruus-6] Bruus, Flensberg (2003). Many-Body Quantum Theory in Condensed Matter Physics: An Introduction. OUP Oxford. ISBN 0198566336.

[Schwabl-7] Schwabl, Hilton, Lahee (2008). Advanced Quantum Mechanics. Springer. ISBN 978-3540850618.{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크)

[8] C. Kurtsiefer, S. Mayer, P. Zarda, Patrick and H. Weinfurter, (2000), "안정적인 단일 광자의 솔리드 스테이트 소스", Phys. 레트 85(2) 290--293, doi 10.1103/PhysRevRevlett.85.290

[9] 산토리, M. 펠튼, G. 솔로몬, Y. 데일, Y. 야마모토(2001), "퀀텀 도트에서 단일 광자 트리거", 물리적 Rev. Let. 86 (8):1502--1505 DOI 10.1103/PhysRevRevlett.86.1502

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Search

포크 상태

네임스페이스

더

목차

정의

두 개의 입자를 사용하는 예제

보소닉 포크 상태

보손 생성 및 소멸 연산자

생성 및 소멸 연산자의 비Hermitity

운영자 ID

특정 Fock 상태에 대한 조치

수 연산자의 작용

보소닉 포크 상태의 대칭 거동

페르미오닉 포크 주

페르미온 생성 및 소멸 연산자

운영자 ID

수 연산자의 작용

최대직업번호

특정 Fock 상태에 대한 조치

페르미오닉 포크 상태의 비대칭 거동

포크 상태는 일반적으로 에너지 고유 상태가 아니다.

진공변동

멀티 모드 포크 상태

단일 광자 상태의 소스

비분류적 행동

참고 항목

참조

외부 링크

Search

포크 상태

정의

두 개의 입자를 사용하는 예제

보소닉 포크 상태

보손 생성 및 소멸 연산자

생성 및 소멸 연산자의 비Hermitity

운영자 ID

N 보소닉 기반 상태 n k 1, n k 2, n k 3 . . . . . . . ⟩ {\displaystyle n_{\mathbf {k}{1}{1},n_{\mathbf {k}{{}}}}{{{}}}},n_{\mathbf{}}}}{}}}}}}}}}}}}}}}}}{{{{{{{{3}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}n_{{\mathbf {k} }_{l},...\rangele }

특정 Fock 상태에 대한 조치

수 연산자의 작용

보소닉 포크 상태의 대칭 거동

페르미오닉 포크 주

페르미온 생성 및 소멸 연산자

운영자 ID

수 연산자의 작용

최대직업번호

N fermionic basises n k 1, n k 2, n k 3 . . . . . . ⟩ {\displaystyle \\n_{{1},n_{\mathbf {k} _{2}},n_{\mathbf {k} _{3}}...n_{\mathbf{k} _{l},...\right\rangele }

특정 Fock 상태에 대한 조치

페르미오닉 포크 상태의 비대칭 거동

포크 상태는 일반적으로 에너지 고유 상태가 아니다.

진공변동

멀티 모드 포크 상태

단일 광자 상태의 소스

비분류적 행동

참고 항목

참조

외부 링크