오각형 이코시테트라헤드론

오각형 이코시테트라헤드론
(모델을 회전하려면 ccw* 또는 cw를 클릭하십시오.)*
유형	카탈루냐 주
콘웨이 표기법	gC
콕시터 다이어그램
면 폴리곤	불규칙한 오각형
얼굴	24
가장자리	60
정점	38 = 6 + 8 + 24
면 구성	V3.3.3.3.4
디헤드각	136° 18' 33'
대칭군	O, ½BC₃, [4,3]⁺, 432
이중 다면체	정육면체를 잘라내다
특성.	볼록, 얼굴-변환, 치랄
그물

Xerardo Neira가 설명한 방법에 따라 Trivonacci 상수(AC)의 기하학적 구조로 나침반과 마크 자로 구성된다.

오각형 이코시트라헤드론 3d 모델

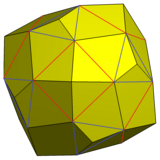
기하학에서, 오각형 이코시테트라헤드론 또는 오각형 이코시카에트라헤드론은^[1] 스너브 큐브의 이중인 카탈로니아 고체다. 결정학에서는 Gyroid라고도 불린다.^[2]^[3]

그것은 두 가지 뚜렷한 형태를 가지고 있는데, 그것은 서로 거울 이미지(또는 "반동형")이다.

건설

오각형 이코시트라헤드론은 듀얼을 사용하지 않고도 스너브 큐브에서 만들 수 있다. 스너브 입방체의 6개의 사각 면에 사각 피라미드가 추가되고, 사각형 면과 모서리를 공유하지 않는 8개의 삼각형 면에 삼각형 피라미드가 추가된다. 피라미드 높이는 스너브 큐브의 다른 24개의 삼각형 면과 일직선으로 되도록 조정된다. 결과는 오각형 이코시트라헤드론이다.

데카르트 좌표, 평행 좌표.

$t\approx 1.839\,286\,755\,21$ $t\approx 1.839\,286\,755\,21$ $t\approx 1.839\,286\,755\,21$ $t\approx 1.839\,286\,755\,21$ $t\approx 1.839\,286\,755\,21$ $(\displaystyle t\$ 약 1 $.839\,286\,755\,21$ 로 트리보나치 상수를 나타낸다(트리보나치 상수에 대한 기하학적 설명은 스너브 큐브 참조). 그 다음 원점을 중심으로 한 오각형 이코시트라헤드론의 38 정점에 대한 데카르트 좌표는 다음과 같다.

(±1, ±(2t+1, ±t²)의 짝수 순열 12개와 짝수 마이너스 부호가 있음
(±1, ±(2t+1, ±t²)의 12개 홀수 순열과 홀수 수의 마이너스 부호가 있음
6개 점³(±t, 0, 0), (0, ±t³, 0) 및 (0, 0, 0, ±t³)
8점(±t², ±t², ±t²)

기하학

The pentagonal faces have four angles of $\arccos((1-t)/2)\approx 114.812\,074\,477\,90^{\circ }$ and one angle of $\arccos(2-t)\approx 80.751\,702\,088\,39^{\circ }$ . 펜타곤에는 각각 3개의 짧은 가장자리가 있고 $(t+1)/2\approx 1.419\,643\,377\,607\,08$ 길이( $(t+1)/2\approx 1.419\,643\,377\,607\,08$ + 1 $(t+1)/2\approx 1.419\,643\,377\,607\,08$ 1.419 $(t+1)/2\approx 1.419\,643\,377\,607\,08$ $(t+1)/2\approx 1.419\,643\,377\,607\,08$ $(t+1)/2\approx 1.419\,643\,377\,607\,08$ $(t+1)/2\approx 1.419\,643\,377\,607\,08$ ${\displaystyle (t+1)/2\$ 약 $1.419\,643\,377\,607\,08}$ 의 긴 가장자리가 있다 $(t+1)/2\approx 1.419\,643\,377\,607\,08$ 예각은 두 긴 가장자리 사이에 있다. 이음각은 $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ ( $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ - $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ / $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ ( $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ - $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ 2 $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ ) $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ ${\$ 약 $136.309\,232\,892\,32^{\circ}}}}$ 에 해당한다 $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$

듀얼 스너브 큐브의 가장자리 길이가 단위인 경우 표면적 및 부피는 다음과 같다.^[4]

{\reasoned}A&=3{\sqrt{\sqrt}{22(5t-1)}{4t-3}&\\\\ 19.299\,94\\\\\V&={\sqrt {\\prac {11(t-4)}{2(20t-37)}}}}&\7.474\end{aigned}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

직교 투영

오각형 이코시테트라헤드론은 정점을 중심으로 하는 두 개의 대칭 위치, 그리고 한 개의 정점 위 대칭 위치가 있다.

직교 투영
투영적 대칭	[3]	[4]⁺	[2]
이미지
이중 이미지

변형

동일한 키랄 팔면 대칭을 가진 등면 변형은 가장자리 길이가 3개인 오각형 면으로 구성할 수 있다.

표시된 변형은 3개의 동일 평면 삼각형이 있는 새로운 삼각형 면들이 동일한 오각형 면으로 통합되도록 6개의 사각형 면과 8개의 삼각형 면에 피라미드를 추가하여 구성할 수 있다.

강화 피라미드와 병합된 면이 있는 스너브 큐브	오각형 이코시테트라헤드론	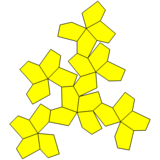그물

관련 다면체 및 틸팅

구면 오각형 이코시테트라헤드론

이 다면체는 다면체 순서와 얼굴 구성의 펜타곤 기울기의 일부로서 위상학적으로 관련이 있다(V3.3.3.3.n). (순서는 쌍곡면을 어떤 n으로 기울이는 것으로 진행된다.) 이 얼굴 변환 수치는 회전 대칭을 가지고 있다.

n32 스너브 틸팅의 대칭 변이: 3.3.3.3.n v t
대칭 n32년	구면				유클리드 주	콤팩트 쌍곡선		파라콤.
대칭 n32년	232	332	432	532	632	732	832	∞32
스너브 수치
구성.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
자이로 수치
구성.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.1987

펜타곤 이코시트라헤드론은 일련의 이중 스너브 폴리헤드 및 얼굴 구성 V3.3.4.3.n이 있는 틸팅에서 두 번째다.

4n2 스너브 틸팅의 대칭 변이: 3.3.4.3.n v t
대칭 4n2	구면		유클리드 주	콤팩트 쌍곡선				파라콤.
대칭 4n2	242	342	442	542	642	742	842	∞42
스너브 수치
구성.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
자이로 수치
구성.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.1987

오각형 이코시테트라헤드론은 정육면체 및 일반 팔면체와 관련된 균일한 다면체의 이중형 중 하나이다.

균일한 팔면체 다면체
대칭: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{3^1,1}

		=	=	=				= 또는	= 또는	=

이중에서 균일한 폴리헤드라까지
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

참조

^ 콘웨이, 사물의 대칭, 페이지 284
^ "Promorphology of Crystals I".
^ "Crystal Form, Zones, & Habit". Archived from the original on 2003-08-23.
^ Eric W. Weisstein, Pentagonal icositetrahedron (Catalan solid) at MathWorld.

Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (제3-9)절)
Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (13반경 볼록 다면체 및 이중체, 28페이지, 펜타곤 이코시테트라헤드론)
2008년 사물의 대칭, 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라우스, ISBN 978-1-56881-220-5 [1] (21장, 아르키메데스 및 카탈로니아 다면체의 명명 및 기울기, 287페이지, 오각형 이코시카이트트라헤드론)