퍼펙트 파이브

Perfect fifth
퍼펙트 파이브
평등한 담금질
정의의
완전 5위
반비례완전 4위
이름
기타 이름디아펜트
약어P5
크기
세미톤7
인터벌 클래스5
just interval3:2
센트
평등한 기질700
그냥 억양701.955
완벽한 다섯 번째 간격의 예

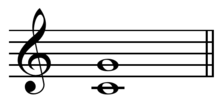
음악 이론에서 완벽한 5번째는 주파수 비율이 3:2인 한 쌍의 투구에 해당하는 음악적 간격이다.

서양 문화에서 온 클래식 음악에서 5번째는 이음계 음계의 연속된 다섯 음의 첫 번째 음에서 마지막 음까지의 간격이다.[1] 완벽한 5번째(흔히 P5)는 7개의 세미톤에 걸쳐 있고, 줄어든 5번째는 6개, 증강 5번째는 8개 세미톤에 걸쳐 있다. 예를 들어, 노트 G는 C 위의 7개 반에 위치하기 때문에 C에서 G까지의 간격은 완벽한 5분의 1이다.

완벽한 5번째는 두 번째와 세 번째 고조파 사이의 간격으로서 고조파 시리즈에서 도출될 수 있다. 이온음계에서는 지배음계가 강장음보다 5분의 1이 더 높다.

완벽한 5번째는 합성과 옥타브를 제외한 다른 어떤 간격보다 자음, 즉 안정적이다. 그것은 모든 장음 및 단음 화음(트라이어드)과 그 확장의 뿌리 위에서 발생한다. 19세기 후반까지, 그것은 종종 그것의 그리스 이름들 중 하나인 디아펜트로 언급되었다.[2] 그것의 역전은 완벽한 4번째다. 다섯 번째 옥타브는 열두 번째다.

완벽한 5번째는 "Twinkle, Twinkle, Little Star"의 시작에 있다; 첫 번째 "Twinkle"의 음은 루트 노트이고 두 번째 "Twinkle"의 음은 그 위의 5번째 음이다.

대체 정의

완벽이라는 용어는 완벽한 5번째를 단순한 피치 관계와 높은 수준의 조화 때문에 부르는 완벽한 간격의 그룹(일립, 완벽한 4번째,옥타브 포함)에 속하는 것으로 식별한다.[3] 피타고라스의 튜닝을 이용해 한 옥타브(피아노 등)에 12음만 내는 악기를 튜닝할 때 125음 중 1음(늑대 5음)이 심하게 불협화음을 내며 '완벽한' 것으로 해석될 경우, 이 용어가 '높은 자음'으로 해석될 경우 거의 '완벽한'이라고 할 수 없다. 그러나 정확한 영건적 철자를 사용할 때, 피타고라스 튜닝이나 의미심장한 기질에서 5번째 늑대는 실제로 완벽한 5번째가 아니라 6번째 감소된 6번째(예: G♯–E♭)이다.

완벽한 간격은 또한 변형이 완벽한 자연적인 간격으로도 정의된다. 여기서 자연적인 경우, 변형이 아닌, 기본 음표와 기본 음표에서 시작하는 주요 이음계 척도의 다른 음표 사이의 간격(예를 들어, C에서 시작하여 C, D, E, F, G, A, B, C까지의 간격, 샤프 또는 플랫이 없는 간격); 이것은 정의된다.인셉션은 일치 정도에 호소하지 않고 일치, 4번째, 5번째, 옥타브만 완벽한 간격을 이끈다.[4]

완벽이라는 용어는 또한 평등한 기질과 같은 다양한 다른 튜닝 시스템에서 "성질" 또는 "불완전한" 작은 정수의 비율에 맞춘 간격을 구별하기 위해 정의의 동의어로 사용되어 왔다.[5][6] 완벽한 합주곡은 1:1의 피칭비, 완벽한 옥타브 2:1, 완벽한 네 번째 4:3, 그리고 완벽한 다섯 번째 3:2를 가지고 있다.

이 정의에서 다른 간격은 완벽한 제3의 간격(5:4)[7] 또는 완벽한 6의 장조 간격(5:3)이라고도 할 수 있다.[8]

기타 자질

완벽함 외에도 5분의 2의 다른 종류, 즉 자질이 있다. 즉 감소된 5분의 1은 더 작은 색채의 세미톤이고, 증강된 5분의 1은 한 색채의 세미톤이 더 큰 것이다. 세미톤 단위로 볼 때, 이것들은 각각 트리톤(또는 증강된 4번째)과 마이너 6번째에 해당한다.

피치비

D에 딱 5점. D 위의 완벽한 5번째(A+, 27/16)는 중간의 C: (AND, 5/3)보다 단지 주요 6번째(AND, 5/3)보다 높은 싱크로닉 쉼표(81/80 또는 21.5 센트)이다.[9]
A 바로 아래 5번째. A(D-, 10/9) 아래의 완벽한 5번째는 just/Pythagorean major caior: (DRG, 9/8)보다 낮은 싱토닉 쉼표다.[9]

정확히 조정된 5분의 1의 음률은 3:2(초기 음악 이론에서도 헤미올라로 알려져 있다)[10][11]로, 즉 윗 음이 아랫 음이 두 개의 음을 내는 것과 같은 시간에 세 개의 진동을 일으킨다는 뜻이다. 바이올린을 튜닝할 때 딱 완벽한 5번째 소리를 들을 수 있는데, 인접한 현을 3:2의 정확한 비율로 조정하면 그 결과는 매끄럽고 자음적인 소리, 그리고 바이올린 소리가 조화롭게 들린다.

피아노와 같은 키보드 악기는 보통 성질이 같은 퍼펙트 5번째 버전을 사용하므로 모든 키에서 연주할 수 있다. 12음 동일 기질에서 담금질 퍼펙트 5의 주파수는 2 ) 7 }}}}{7 또는 약 1.498307이다. 700센트로 정의되는 똑같이 담금질된 완벽한 5번째는 약 701.955센트로 정의되는 완벽한 5번째보다 약 2센트가 더 좁다.

케플러는 정수비 측면에서 음악적 튜닝을 탐구했고, "낮은 불완전한 5위"를 40:27 피칭비로, "더 큰 불완전한 5위"를 243:160 피칭비로 정의했다.[12] 그의 완벽한 5번째 비율인 1.48148(680센트)은 1.4983(이상 1.50에 상대적)의 동일 기질 튜닝(700센트)보다 훨씬 더 '불완전'하다. 헤르만 폰 헬름홀츠(Hermann von Helmholtz)는 불완전한 5분의 1의 비율로 301:200 (708 센트)의 비율을 사용하며, 동일 기질에서의 5분의 1의 비율과 "완벽한 5분의 1"(3:2)을 대조하고, 그러한 "불완전한" 튜닝에서 비롯되는 비트의 청각성을 논한다.[13]

조화롭게 사용

W. E. 히스코테는 옥타브가 삼합체 내의 일차적 단결을 나타내는 것으로서, 연속적인 과정으로부터 생성된 더 높은 단결인 "첫 번째 옥타브, 그 다음 다섯 번째, 그리고 세 번째, 두 번째 옥타브의 결합"이라고 설명한다.[14] 헤르만 폰 헬름홀츠는 그의 책의 영어 번역 편집자가 4번째와 5번째는 서로 교환할 수 없거나 확실하지 않을 수 있지만, 완벽한 4번째, 5번째, 옥타브 같은 어떤 간격은 "알려진 모든 음악적 음계에서 발견된다"고 주장한다.[15]

완벽한 5번째는 장·단기 트라이어드 건설과 그 확장의 기본 요소다. 이러한 화음은 많은 음악에서 자주 발생하기 때문에 완벽한 5번째 화음은 그만큼 자주 발생한다. 그러나 많은 악기들이 오버론으로서 완벽한 5분의 1을 포함하고 있기 때문에 화음(특히 뿌리 위치)의 5분의 1을 생략하는 것은 예사롭지 않다.

완벽한 5번째는 "큰 테르티안" 하모니뿐만 아니라 7번째 화음에도 존재한다. (뿌리 3분의 1에 4개 이상의 톤으로 구성된 조화) 완전한 5분의 2의 존재는 사실 이러한 화음의 불협화음 간격을 부드럽게 할 수 있는데, 그것은 대 7분의 2의 불협화음이 두 개의 완벽한 5분의 2의 존재에 의해 부드러워지는 주요한 7번째 화음에서와 같다.

화음은 5중으로 쌓아서 5중 하모니를 만들어 낼 수도 있다. 그러한 하모니는 폴 힌데미스의 음악과 같은 좀 더 현대적인 음악에 존재한다. 이 조화는 또한 "청소년들의 춤"에서 스트라빈스키의 "봄의 의식"에도 나타나는데, 4개의 C 트럼펫과 피콜로 트럼펫, 1개의 뿔이 5단 B-플랫 5중창을 연주한다.[16]

베어 파이브, 오픈 파이브 또는 비어 있는 파이브

8번째 음의 E5 전원 코드

맨 5번째, 열린 5번째 또는 비어있는 5번째는 3번째가 없는 완벽한 5번째만 포함하는 화음이다. 페로틴의 비데룬트 옴므와 세데룬트 프린세스, 기욤 드 마하우트의 메세 드 노스트레 데임, 모차르트 레퀴엠의 키리, 브루크너 9번 교향곡의 제1악장은 모두 열린 5회에서 끝나는 곡들의 예들이다. 이러한 화음은 중세 음악, 신성한 하프 노래, 그리고 록 음악 전반에 공통적이다. 하드 록, 메탈, 펑크 음악에서, 과하게 움직이거나 왜곡된 일렉트릭 기타는 3분의 1을 진흙으로 만들 수 있고, 5분의 1은 바삭바삭하다. 또한 빠른 화음 기반 구절은 가장 흔한 4개의 기타 손 모양을 하나로 결합하여 연주하기 쉽게 만들어진다. 록 뮤지션들은 그들을 파워 코드라고 부른다. 전력 화음은 종종 옥타브 더블링(즉, 베이스 음은 한 옥타브 더 높게 2배 더 높게, 예를 들어 F3–C4–F4)을 포함한다.

파차시쿠
캉투

빈 5위는 전통 음악, 예를 들어 아시아 음악, 그리고 칸투와 시쿠리와 같은 콜럼비아 이전의 안데스 음악 장르에서 사용된다. 모든 곡에서 같은 선율이 5와 옥타브 평행으로 리드되고 있다.

서양 작곡가들은 그 구절을 이국적인 풍미를 주기 위해 그 간격을 사용할지도 모른다.[17] 비어 있는 5번째는 또한 간성에게 모호한 품질을 주기 위해 사용되기도 하는데, 이는 맨 다섯 번째가 중대하거나 사소한 톤수를 나타내지 않기 때문이다.

튜닝 및 톤 시스템 사용

옥타브와 함께 딱 완벽한 5번째는 피타고라스 튜닝의 기초를 이룬다. 약간 좁혀진 완벽한 5번째도 하나의 조정의 기초가 된다.[citation needed]

5초 원은 색소음계(색소원)를 위한 음치 공간의 모델로서, 근접성을 색소음 인접성이 아닌 음표에서 다른 음표까지 얻는 데 필요한 완벽한 5초 수로 간주한다.

참고 항목

참조

  1. ^ 돈 마이클 랜델(2003) 하버드대 음악사전 인터벌 4판(매사추세츠주 캠브리지: 하버드 대학 출판부: 페이지 413.
  2. ^ William Smith; Samuel Cheetham (1875). A Dictionary of Christian Antiquities. London: John Murray. p. 550. ISBN 9780790582290.
  3. ^ Piston, Walter; DeVoto, Mark (1987). Harmony (5th ed.). New York: W. W. Norton. p. 15. ISBN 0-393-95480-3.. 옥타브, 완벽한 간격, 3분의 1과 6분의 1은 "상호간격"으로 분류되지만, 3분의 3과 6분의 1은 "불완전한 조화"로 적격이다.
  4. ^ Kenneth McPherson Bradley (1908). Harmony and Analysis. C. F. Summy. p. 17.
  5. ^ Charles Knight (1843). Penny Cyclopaedia. Society for the Diffusion of Useful Knowledge. p. 356.
  6. ^ John Stillwell (2006). Yearning for the Impossible. A. K. Peters. p. 21. ISBN 1-56881-254-X. perfect fifth imperfect fifth tempered.
  7. ^ Llewelyn Southworth Lloyd (1970). Music and Sound. Ayer Publishing. p. 27. ISBN 0-8369-5188-3.
  8. ^ John Broadhouse (1892). Musical Acoustics. W. Reeves. p. 277. perfect major sixth ratio.
  9. ^ a b John Fonville (Summer 1991). "Ben Johnston's Extended Just Intonation: A Guide for Interpreters". Perspectives of New Music. 29 (2): 109 (106–137). JSTOR 833435.
  10. ^ Willi Apel (1972). "Hemiola, hemiolia". Harvard Dictionary of Music (2nd ed.). Cambridge, Massachusetts: Harvard University Press. p. 382. ISBN 0-674-37501-7.
  11. ^ Randel, Don Michael, ed. (2003). "Hemiola, hemiola". Harvard Dictionary of Music (4th ed.). Cambridge, Massachusetts: Harvard University Press. p. 389. ISBN 0-674-01163-5.
  12. ^ Johannes Kepler (2004). Stephen Hawking (ed.). Harmonies of the World. Running Press. p. 22. ISBN 0-7624-2018-9.
  13. ^ Hermann von Helmholtz (1912). On the Sensations of Tone as a Physiological Basis for the Theory of Music. Longmans, Green. pp. 199, 313. perfect fifth imperfect fifth Helmholtz tempered
  14. ^ W. E. 히스코트 (1888), "Introposprivation Ecripty" (The Nature of Harmony and Metre)에서 W. E. 히스코트 (London: Swan Sonnenschein) p. xx가 번역 및 편집했다.
  15. ^ Hermann von Helmholtz (1912). On the Sensations of Tone as a Physiological Basis for the Theory of Music. Longmans, Green. p. 253. perfect fifth imperfect fifth Helmholtz tempered
  16. ^ 피스톤 & 드보토 1987, 페이지 503–505.
  17. ^ 2012년 12월 28일 뉴라인 극장의 "왕의 내부" 스콧 밀러