
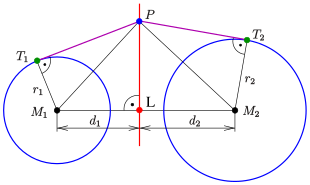
두 원 외부의 P 은 접선 거리(보라색)가 같으면 급진 축(빨간색
P 은 접선 거리(보라색)가 같으면 급진 축(빨간색 에 놓여 있다: 1= = } . P , , T {\ P}}개가 공통 접선 위에 놓여
에 놓여 있다: 1= = } . P , , T {\ P}}개가 공통 접선 위에 놓여 있다면, 은 1, }}의 중간점이다
있다면, 은 1, }}의 중간점이다 .
. 기하학에서 두 개의 비집중 원의 급진적인 축은 원과 관련된 힘이 같은 점들의 집합이다. 이러한 이유로 급진축을 두 원의 동력선 또는 동력 이등분자라고도 한다. 자세한 내용:
의 , 2 {\},}}의 경우 , 중심 M 1, M 2 M_{1}, }} 및
, 중심 M 1, M 2 M_{1}, }} 및 반지i },2}} 원에 대한
반지i },2}} 원에 대한 점 의 힘은
점 의 힘은 다음과 같다
다음과 같다
 .
.
점 은(는) 과격한 축에 속한다 .
.
- ( )= ( P)
 .
.
원의 공통점이 두 개라면, 급진적인 축은 원의 공통적인 제분선이다.
점 이(가) 원 외부에 있는 경우, {\P}은 두 원과 접선 거리가 같다
경우, {\P}은 두 원과 접선 거리가 같다 .
.
반지름이 같을 경우, 은 M1,M 2 {\ M_{1}}의 선 세그먼트 이등분자 입니다
어쨌든 급진축은 M 의 {2}}에 수직인 선이다
- 공지에 관하여
프랑스 수학자 M이 과격축이라는 표기법을 사용했다. 도끼처럼 과격하다. [1]
J.V. 폰셀렛은 코드 이데일을 사용했다. [2]
J. 플뤼커는 코달레라는 용어를 소개했다.[3]
J. Steiner는 동력의 과격한 축선(Linie der gleichen Potenzen)을 칭하여 전력선(Potenzgerade)으로 이어졌다.[4]
특성.
기하학적 형태와 그 위치
 →, → 1, m→ vec vec _{1},{\ {{m}2}} },
→, → 1, m→ vec vec _{1},{\ {{m}2}} }, 그러면 그 래디컬 라인의 정의 방정식을 다음과 같이 작성될 수 있다.
그러면 그 래디컬 라인의 정의 방정식을 다음과 같이 작성될 수 있다.

d , }}의 정의 및 계산 올바른 방정식에서 얻은 것이다.
- 급진축의 점 집합은 실로 선이며 권선 중심을 통과하는 선에 수직이다.
(→ - → 1 }는 래디컬 축에 대한 정상적인 벡터!)
래디컬 축에 대한 정상적인 벡터!)
방정식을 →→ 2로 나누면 헤시안 정규 형태를 얻게 된다 중심 위치 벡터를 삽입하면 중심에서 급진 축까지의 거리가 발생한다.
중심 위치 벡터를 삽입하면 중심에서 급진 축까지의 거리가 발생한다.
 ,
,- = M2 {\d=2}
 .
.
( L 이 (가) ,M 2}} 에 있지 않으면 음수가 될 수 있다
(가) ,M 2}} 에 있지 않으면 음수가 될 수 있다 .)
.)
원들이 두 지점에서 교차하는 경우, 급진적인 선은 공통점을 통과한다. 서로 만질 수만 있다면 그 급진적인 선은 흔히 접선하는 선이다.
특수 포지션
- 두 개의 교차하는 원들의 급진적인 축은 그들의 공통적인 제분선이다.
- 두 개의 만지는 원의 급진적인 축은 그들의 공통 접선이다.
- 두 개의 비교차 원의 급진적인 축은 두 개의 편리한 장비 원(아래 참조)의 공통점이다.
직교 원

을(를) 통과하는 접선의 접촉점은 직교 원(녹색)에 위치한다 .
. - 원 밖에
 있는 점 과
있는 점 과 (와) 두 접선 점 의 경우 방정식
(와) 두 접선 점 의 경우 방정식 P 2= T 2= ( P) ^{}}는 고정되고
P 2= T 2= ( P) ^{}}는 고정되고 , T 은
, T 은 는) P 및 반지름
는) P 및 반지름 radius {\sqrt
radius {\sqrt  을
을 {\i}}}}}}}}}은 직교차한다
{\i}}}}}}}}}은 직교차한다
 . 따라서 다음과 같다.
. 따라서 다음과 같다.
- If
 is a point of the radical axis, then the four points
is a point of the radical axis, then the four points  lie on circle
lie on circle  , which intersects the given circles
, which intersects the given circles  orthogonally.
orthogonally.
- 급진축은 모든 원의 중심들로 구성되며, 이는 주어진 원을 직교적으로 교차한다.
직교 원 계통
직교적으로 두 개의 원과 교차하는 원 연필을 만들기 위해 이전 절에서 설명한 방법은 원과 직교하는 두 개의 원과 교차하는 시스템을 구성하기 위해 확장될 수 있다.[5][6]
, }}개의 누운 원(앞부분과 같이), , , 1, 2}}개의 중심과 radi 및 급진적인
중심과 radi 및 급진적인 축을 두십시오
축을 두십시오 . 이제 모든 원은 c 2}}:
. 이제 모든 원은 c 2}}: c 1 {\과
c 1 {\과 (와 함께 라디컬 축으로
(와 함께 라디컬 축으로 구성된 과 된다 }가 그러한
구성된 과 된다 }가 그러한 원인 경우, 중심은
원인 경우, 중심은  M 반경
M 반경 2
2  앞의 결과에서 방정식을 얻는다.
앞의 결과에서 방정식을 얻는다.
- }}:{
 여기서 > r }>은(는) 고정되어 있다
여기서 > r }>은(는) 고정되어 있다 .
.
= - 1}를 하여 방정식을 다음과 같이 다시 쓸 수 있다.
같이 다시 쓸 수 있다.
- = - r + 2{\}^{1}^{}+\}^{2}^{2}^{2}^{2}^{

반지름 2}}이 주어진 경우, 이 방정식에서 }} ~ (고정) 새 중심부의 (고정)급극축까지의 거리
경우, 이 방정식에서 }} ~ (고정) 새 중심부의 (고정)급극축까지의 거리 Δ 2{\displaystysty \delta_{2}}. 도표에서 새 원의 색은 보라색이다. 모든 녹색 원(도표 참조)은 그 중심이 급진 축에 있고 원 c , 2 }}회 직교적으로
Δ 2{\displaystysty \delta_{2}}. 도표에서 새 원의 색은 보라색이다. 모든 녹색 원(도표 참조)은 그 중심이 급진 축에 있고 원 c , 2 }}회 직교적으로 교차하며, 따라서 모든 새로운 원(보라색)도 교차한다. (빨간색)급수축을 y축으로, 라인 M 1} x축으로
교차하며, 따라서 모든 새로운 원(보라색)도 교차한다. (빨간색)급수축을 y축으로, 라인 M 1} x축으로 선택하면 원의 두 연필에는 다음과 같은 방정식이 있다.
선택하면 원의 두 연필에는 다음과 같은 방정식이 있다.
- 보라색:( - ) 2+ = + r -d \\ (

- : 2+ (y- ) 2= y 2+ d - r . \

(( , y ) (은 녹색 원의 중심이다.)
녹색 원의 중심이다.)
속성:
a) 두 의 녹색 원은 원 직교 시스템의 극인 / 2= 1 - r , 0 }^{에서 X 축에 교차한다. 즉, x축은 그린 서클의 급진적인 선이라는 뜻이다.
/ 2= 1 - r , 0 }^{에서 X 축에 교차한다. 즉, x축은 그린 서클의 급진적인 선이라는 뜻이다.
b) 보라색 원은 공통점이 없다. But, if one considers the real plane as part of the complex plane, then any two purple circles intersect on the y-axis (their common radical axis) at the points  .
.
특별한 경우:
a) d = 1}의 경우 녹색 원은 x축을 공통 접선으로 하여 원점에서 서로 접촉하고 보라색 원은 y축을 공통 접선으로 한다. 이러한 원형의 체계를 동축 포물선(아래 참조)이라고 한다.
원은 x축을 공통 접선으로 하여 원점에서 서로 접촉하고 보라색 원은 y축을 공통 접선으로 한다. 이러한 원형의 체계를 동축 포물선(아래 참조)이라고 한다.
b) c }를 중심
 즉 1= 0 으로 축소하면
즉 1= 0 으로 축소하면 방정식이 보다 단순한 형태로 변하며 M = 1{\
방정식이 보다 단순한 형태로 변하며 M = 1{\ }.
}.
결론:
a) 모든 실제 원 연필

- 자산 보유: y축은 ( 1), ( ) c의 과격한 축이다

- > 의 경우
 c( 1), 2) c가 / =( ± (
c( 1), 2) c가 / =( ± ( 에서 교차한다
에서 교차한다 .
. - < 의 경우 공통점이
 없다.
없다. - = 의 경우(, ) 에서 터치하고

 y축은 공통 접선이다.
y축은 공통 접선이다.
b) 실제 원 연필 두 자루


- 직교 원형을 이루다 즉, 두 원 c (), () 이(가) 직교한다
 .
.
c) b)의 방정식에서 좌표 자유 표현을 얻는다.

주어진 극 , }}에 대한 원의 직교계 - 주어진 P , 2
 중간 지점 및
중간 지점 및 라인 세그먼트 이등분 g 에
라인 세그먼트 이등분 g 에 대해 두 방정식
대해 두 방정식 

- P 에

 그러나 에
그러나 에 1, P 2 {\
1, P 2 {\ N N 사이는 아니다
N N 사이는 아니다 - 시스템의 극인
 ,P }에 의해 고유하게 결정되는 원의 직교 시스템을 설명한다.
,P }에 의해 고유하게 결정되는 원의 직교 시스템을 설명한다. - = 2= O 의 경우 시스템의

 , }}개도 처방해야 한다. 이 시스템은 포물선이다.
, }}개도 처방해야 한다. 이 시스템은 포물선이다. 

 {\}에 M
{\}에 M 
 }}에 N 포함.
}}에 N 포함.
직선 및 나침반 구조:
직교 원 시스템은 극 , 
- 축(라디칼 축)은 극의
 P }}: 라인 세그먼트 이등분자 이다
P }}: 라인 세그먼트 이등분자 이다 .
. - 원(도표에서 녹색)은P , 2 중심은 g 에 있다

 그것들은 쉽게 그려질 수 있다. N 의 경우 반지름은
그것들은 쉽게 그려질 수 있다. N 의 경우 반지름은 N= 입니다
N= 입니다
- In order to draw a circle of the second pencil (in diagram blue) with center
 on
on  , one determines the radius
, one determines the radius  applying the theorem of Pytagoras: 도표 참조).
applying the theorem of Pytagoras: 도표 참조).
= }}개의 경우 축을 추가로 선택해야 한다. 그 시스템은 포물선이고 쉽게 그릴 수 있다.
추가로 선택해야 한다. 그 시스템은 포물선이고 쉽게 그릴 수 있다.
동축원
정의 및 속성:
, }를 두 개의 원으로 하고 , }}개의
원으로 하고 , }}개의 전원 기능을 한다. 그런 다음 의 경우
전원 기능을 한다. 그런 다음 의 경우

원 () 의 방정식이다( 아래 참조). 그러한 원의 시스템을 원 1, }}
아래 참조). 그러한 원의 시스템을 원 1, }} . (= = {\}의
. (= = {\}의 경우 은 c, 2{\}} .)의 과격한 축을 설명한다.
경우 은 c, 2{\}} .)의 과격한 축을 설명한다.
() 의 전원 함수는
 .
.
규범 방정식( , 2 x 계수는  (의
(의  은
은  (λ, x )= 0
(λ, x )= 0 
간단한 계산은 다음을 나타낸다.
- ( ), c() , c(\\\ \은 1, c c_2}}와인 축을 가지고 있다


이 (가) 무한대로 이동할 수 있도록 허용하면 , = ( 의 동축 원 시스템의 구성원이라는
(가) 무한대로 이동할 수 있도록 허용하면 , = ( 의 동축 원 시스템의 구성원이라는 것을 인식하게 된다
것을 인식하게 된다
(E): If  intersect at two points
intersect at two points  , any circle
, any circle  contains
contains  , too, and line
, too, and line  is t공동 급진 축 이런 시스템을 타원체라고 한다.
is t공동 급진 축 이런 시스템을 타원체라고 한다.
(P): 1, }}: 에서 접선된 경우
 원은 ,c 2 {\
원은 ,c 2 {\ 1},2}}: P 에서도
1},2}}: P 에서도 접선된다. 공통 접선은 그들의 공통적인 급진적 축이다. 그런 시스템을 포물선이라고 한다.
접선된다. 공통 접선은 그들의 공통적인 급진적 축이다. 그런 시스템을 포물선이라고 한다.
(H): 1,c }}: 공통점이 없는 경우, 시스템 쌍도 동일하다. 어느 한 쌍의 원의 급진적인 축은 , 2}}의 급진적인 축이다
경우, 시스템 쌍도 동일하다. 어느 한 쌍의 원의 급진적인 축은 , 2}}의 급진적인 축이다 그 시스템은 쌍곡선이라고 불린다.
그 시스템은 쌍곡선이라고 불린다.
자세한 내용:
다음과 같은 좌표 소개


그 다음 y축은 그들의 급진적인 축이다(위 참조).
전원 함수 , , y) 을 계산하면 다음과 같은 표준 원 방정식이 제공된다 .
.

정사각형 및 = - d2 1 - {\2}={\ {1}-\ 중앙의 x 좌표)를 완성하면 방정식의 중심 형식이 산출된다.
중앙의 x 좌표)를 완성하면 방정식의 중심 형식이 산출된다.

> 1 }의 경우 ,c ,c () 원은 두 점을
두 점을 가진다.
가진다.

공통적으로 동축 원의 체계는 타원형이다.
r = 디스플레이 스타일 }{1}의 경우, 원 c , ,c () (\lambda 는 점
점 = ( 0 (의 공통점을 가지며
= ( 0 (의 공통점을 가지며 시스템이 포물선이다.
시스템이 포물선이다.
< }<1}{1}의 경우 원  1, , () 는 공통점이 없고 시스템이
1, , () 는 공통점이 없고 시스템이 쌍곡성이다.
쌍곡성이다.
대체 방정식:
1) 원의 동축계 정의방정식에서는 동력함수의 배수를 사용할 수도 있다.
2) 원 중 하나의 방정식은 원하는 급진축의 방정식으로 대체할 수 있다. 급진축은 반지름이 무한히 큰 원형으로 볼 수 있다. 예를 들면 다음과 같다.


첫 번째 원과 선 x= 2 }}을 래디컬 축으로 하는 모든 원을 설명한다.
하는 모든 원을 설명한다.
3) 두 원의 동등한 지위를 표현하기 위하여, 다음의 형태를 자주 사용한다.

그러나 이 경우, , 매개 변수에 의한 원의 표현은 고유하지 않다.
않다.
응용 프로그램:
a)순환과 뫼비우스 변환은 각도와 일반화된 원을 보존한다. 따라서 원의 직교 시스템은 이러한 매핑에 대한 조사와 함께 필수적인 역할을 한다. [9][10]
b) 전자기학에서는 동축 원이 필드 라인으로 나타난다. [11]
의 급적의 급,, 적의의 건 construction의 .

3개의 원의 급진적 중심 녹색 원은 세 원과 직교적으로 교차한다. - For three circles
 , no two are concentric, there are three radical axis
, no two are concentric, there are three radical axis  . If the circle centers lie not on a line, the radical axes intersect in a common point
. If the circle centers lie not on a line, the radical axes intersect in a common point  , the radical cent3개의 원 중에서 두 원의 직교원(방사선원)도 세 번째 원과 직교한다.
, the radical cent3개의 원 중에서 두 원의 직교원(방사선원)도 세 번째 원과 직교한다.
- 교정: rodical 축 에는 c k {\k}}}와 접선 거리가 같은 모든 점이 포함되어
 있다
있다 와
와 의
의 교차점 은 세 원 모두에 대해 접선 거리가 동일하다
교차점 은 세 원 모두에 대해 접선 거리가 동일하다 . 따라서 도 급진축 g 의 지점이다
. 따라서 도 급진축 g 의 지점이다

- 이 속성은 두 개의 비 교차 원 c , 2 }}
 : , 2 }를 교차하는, 주어진 중심에 중앙이 아닌
: , 2 }를 교차하는, 주어진 중심에 중앙이 아닌 세 번째 원 3을 그릴 수 있다
세 번째 원 3을 그릴 수 있다 래디컬 축 , 을(를) 그릴 수 있다
래디컬 축 , 을(를) 그릴 수 있다 . 이들의 교차점은 세 원 중 급진적
. 이들의 교차점은 세 원 중 급진적 R 이며 g 에 놓여 있다
R 이며 g 에 놓여 있다 의 displaystyle {\}}에 수직인
의 displaystyle {\}}에 수직인  을 통과하는 선은 급진축 g 이다
을 통과하는 선은 급진축 g 이다

추가 시공 방법:

동그라미 , c }}개의 동력이 있는 급진축의 구성. ( 1)= ( P ) 이다
동력이 있는 급진축의 구성. ( 1)= ( P ) 이다
주어진 c 에 동일한 힘을 가진 모든 지점은 에 동심원으로 있는 원 위에 놓여 있다
 그것을 등전원 원이라고 부르자. 이 속성은 두 개의 원의 급진적인 축의 추가 시공 방법에 사용할 수 있다.
그것을 등전원 원이라고 부르자. 이 속성은 두 개의 원의 급진적인 축의 추가 시공 방법에 사용할 수 있다.
두 개의 비 교차 원 , c 1 c 2 c c 1, 2 {\},2 c c, }를 그릴 수 있다
c c, }를 그릴 수 있다 (
( 도 참조). In detail:
도 참조). In detail:  . If the power is large enough, the circles
. If the power is large enough, the circles  have two points in common, which lie on the radical axis
have two points in common, which lie on the radical axis  .
.
양극 좌표와의 관계
일반적으로 두 개의 분리된 비집중 원은 양극 좌표계의 원과 정렬할 수 있다. 이 경우, 급진적인 축은 단순히 이 의 y y - 축이다 . 좌표계의 두 초점을 통과하는 축의 모든 원은 두 원과 직교적으로 교차한다. 원들의 최대 집합은 모두 주어진 선에 중심을 두고 있고 모든 쌍이 같은 급진적인 축을 가지고 있는 것으로, 동축 원의 연필로 알려져 있다.
. 좌표계의 두 초점을 통과하는 축의 모든 원은 두 원과 직교적으로 교차한다. 원들의 최대 집합은 모두 주어진 선에 중심을 두고 있고 모든 쌍이 같은 급진적인 축을 가지고 있는 것으로, 동축 원의 연필로 알려져 있다.
삼선 좌표에서의 급진적 중심
원들이 일반적인 방법으로 삼선 좌표로 표현된다면, 그들의 급진적인 중심은 어떤 결정요인으로 편리하게 주어진다. 특히 X = x : y : z는 세로 길이 a = BC, b = CA, c = AB , 삼각형 ABC 평면의 변수 점을 나타내며 다음과 같이 원을 나타낸다.
- (dx + eye + fz)(ax + by + cz) + g(ayz + bzx + cxy) = 0
- (hx + iy + jz)(ax + by + cz) + k(ayz + bzx + cxy) = 0
- (lx + my + nz)(ax + by + cz) + p(ayz + bzx + cxy) = 0
그렇다면 급진적인 중심이 요점이다.

래디컬 평면 및 하이퍼플레인
3차원의 두 비원성 구의 급진적 평면은 유사하게 정의된다: 그것은 두 구에 대한 접선의 길이가 같은 지점들의 중심이다.[12] 이 중심점이 평면이라는 사실은 급진적인 축이 직선이라는 사실에서 3차원에서 회전하면서 따라온다.
어떤 차원에서도 유클리드 공간의 하이퍼스피어에도 동일한 정의를 적용할 수 있어 두 개의 비원성 하이퍼페어의 급진적 하이퍼플레인(hyperplane)을 부여한다.
메모들
- ^ 미셸 샤슬스, C. H. 슈누제: Die Grundlehren der Neuern Geometrie, Erster Theil, Verlag Leibrock, Braunschweig, 1856, 페이지 312
- ^ 피셔 박사: Lehrbuch der Analysische Geometrie, Darmstadt 1851, Verlag Ernst Kern, 페이지 67
- ^ H. 슈바르츠: 다이 엘리먼트 데어 분석가 지오메트리 데어 에베네, Verlag H. W. 슈미트, 할레, 1858년, 페이지 218
- ^ 제이콥 스타이너: 에이네게 기하학적 구조 베트라흐퉁엔 인: Journal für die reine und Angelwandte Mathetik, 밴드 1, 1826, 페이지 165
- ^ A. Schenfliess, R. Courant: Einführung in die Analytische Geometrie der Ebene und des Raumes, Springer-Verlag, 1931, 페이지 113
- ^ C. 카라테오도리: 펑크티온텐테오리, 비르카유저-베를라크, 바젤, 1961년 ISBN 978-3-7643-0064-7,p. 46
- ^ 댄 페도: 원: 수학적 관점, 미국수학협회, 2020, ISBN 9781470457327, 페이지 16
- ^ 라클란: 현대 순수 기하학, 맥밀란&코, 뉴욕, 1893, 페이지 200에 관한 기초 논문
- ^ 카라테오도리: 펑키온티허리 47쪽
- ^ R. Sauer: Ingenieur-Mathematik: Zweiter 밴드: Differentleichungen und Funktionentheuri, Springer-Verlag, 1962년 ISBN 978-3-642-532-0, 페이지 105
- ^ 클레멘스 셰이퍼: 엘렉트로다이나믹 und Optik, Verlag: 드 그루이터, 1950년 ISBN 978-3-11-230936-0, 페이지 358.
- ^ 메리암-웹스터 온라인 사전.
참조
추가 읽기
외부 링크
 | 위키미디어 커먼스는 급진적 도끼와 관련된 미디어를 보유하고 있다. |


















 (가)
(가) 


 (와) 두 접선 점
(와) 두 접선 점 






 (와
(와











 녹색 원의 중심이다.)
녹색 원의 중심이다.) 












































 (가) 무한대로 이동할 수 있도록 허용하면
(가) 무한대로 이동할 수 있도록 허용하면 









 점
점





 않다.
않다. 
















