This is a good article. Click here for more information.

가역성 셀룰러 오토매틱

Reversible cellular automaton
9개의 상태를 가진 1차원 반전성 셀룰러 오토매틱.각각의 단계에서, 각각의 세포는 왼쪽 이웃으로부터 모양을 복사하고 오른쪽 이웃으로부터 색을 복사한다.

가역형 셀룰러 자동화는 모든 구성이 독특한 전임자를 갖는 셀룰러 자동이다.즉, 업데이트 전 모든 셀의 이전 상태가 모든 셀의 업데이트된 상태로부터 고유하게 결정될 수 있도록 주변의 상태에 기초하여 모든 셀을 동시에 업데이트하는 규칙을 가진, 각각 유한한 상태 집합에서 추출한 상태를 포함하는 정기적인 셀 격자다.가역형 셀룰러 자동화의 시간 역학관계는 아마도 훨씬 더 큰 이웃에 있는 또 다른 셀룰러 자동규칙에 의해 항상 설명될 수 있다.

여러 가지 방법으로 셀룰러 오토마타 규칙을 되돌릴 수 있는 것으로 알려져 있는데, 여기에는 각각의 업데이트가 셀을 블록으로 분할하여 각 블록에 개별적으로 회전할 수 없는 기능을 적용하는 블록 셀룰러 오토매틱 방법과 업데이트 규칙이 두 pr의 상태를 결합한 2차 셀룰러 오토매틱 방법이 포함된다.자동화의 기이한 걸음걸이자동화가 이러한 방법 중 하나로 정의되지 않고 대신 규칙 테이블로 주어지는 경우, 가역성 여부를 시험하는 문제는 블록 셀룰러 오토마타와 1차원 셀룰러 오토마타에 대해 해결할 수 있지만, 다른 유형의 셀룰러 오토마타에 대해서는 해석할 수 없다.

가역성 셀룰러 오토마타는 가역성 컴퓨팅의 자연스러운 모델을 형성하는데, 이는 초저전력 컴퓨팅 장치로 이어질 수 있는 기술이다.양자역학의 원리를 이용하여 계산을 수행하는 한 가지 방법인 양자 세포 자동화는 종종 되돌릴 수 있어야 한다.또한 이상적인 기체에서의 입자의 움직임이나 자기 전하의 정렬의 Ising 모델과 같은 물리적 모델링의 많은 문제들은 자연적으로 되돌릴 수 있으며, 가역성 세포 자동화에 의해 시뮬레이션될 수 있다.

가역성과 관련된 특성은 전체 구성 공간에서 가역할 수는 없지만 초기에는 모든 임의 구성이 수렴하는 유인기로서 구성 공간의 하위 집합을 갖는 세포 자동화를 연구하는데 사용될 수 있다.Stephen Wolfram은 "어느 시스템이든 끌어당기는 자에 한 번, 되돌릴 수 있는 기본 규칙이 없더라도, 어떤 의미에서는 대략적인 가역성을 보여주어야 한다"[1]고 썼다.

예

1차원 오토마타

세포 자동화는 세포(종종 1차원 또는 2차원 배열), 각 세포에 들어갈 수 있는 유한한 값이나 상태의 집합, 각 셀을 한정된 세트의 인근 세포와 연관시키는 근린, 그리고 모든 세포의 값이 동시에 nei 값의 함수로 업데이트되는 업데이트 규칙에 의해 정의된다.징징거리는 세포가장 간단한 셀룰러 오토마타는 1차원 셀 배열을 가지고 있으며, 각각 0 또는 1의 이진값을 가질 수 있으며, 각각의 셀은 그것과 그것의 가장 가까운 두 개의 셀로 구성된 이웃을 양쪽에 가지고 있다. 이것들은 기본 셀룰러 오토마타라고 불린다.[2]그러한 자동화에 대한 업데이트 규칙이 각 셀이 항상 동일한 상태로 유지되도록 하는 경우, 자동은 되돌릴 수 있다. 즉, 각 셀의 이전 상태와 현재 상태가 같기 때문에 모든 셀의 이전 상태를 현재 상태에서 복구할 수 있다.마찬가지로 업데이트 규칙으로 인해 모든 셀이 0에서 1로, 그 반대로 상태가 변경되거나, 셀이 고정된 인접 셀로부터 상태를 복사하도록 하거나, 또는 상태를 복사한 다음 그 값을 역전시키는 원인이 되는 경우에는 반드시 되돌릴 수 있다.[3]토폴리와 마골루스(1990년)는 이러한 종류의 가역성 세포 자동화를 각 세포의 상태가 단지 하나의 이웃한 세포의 이전 상태인 "십이성"에만 의존하는 것으로 부른다.그 단순함에도 불구하고, 각 세포가 이웃 세포의 상태를 모방하게 하는 업데이트 규칙은, 시프트 맵으로 알려진 기호 역학 이론에서 중요하다.[4]

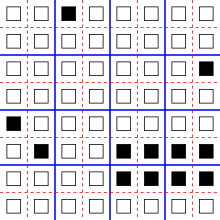
조금 덜 사소한 것으로, 셀이 다시 1차원 배열을 형성하지만, 각 상태는 왼쪽 부분 l와 오른쪽 부분 r로 구성된 순서 쌍(l,r)이며 각각 가능한 값의 유한 집합에서 도출된다고 가정한다.셀의 왼쪽 부분을 왼쪽 이웃의 왼쪽 부분으로, 그리고 오른쪽 이웃의 오른쪽 부분으로 설정하는 전환 함수를 정의한다.즉, 왼쪽 이웃의 상태가 (a,b)이고 오른쪽 이웃의 상태가 (c,d)인 경우, 세포의 새로운 상태는 (a,b)× (c,d) = (,d)로 정의된 쌍방향 연산 ×를 사용하여 이러한 상태를 결합한 결과물이다.이 구조의 예는 그림에서 제시되는데, 왼쪽 부분은 형상으로 그래픽으로 표현되고 오른쪽 부분은 색상으로 표현된다. 이 예에서 각 셀은 왼쪽 이웃의 모양과 오른쪽 이웃의 색상으로 업데이트된다.그러면 이 자동화는 되돌릴 수 있다: 각 쌍의 왼쪽에 있는 값이 오른쪽으로 이동하고 오른쪽에 있는 값이 왼쪽으로 이동하므로, 각 셀의 이전 상태는 인접한 셀에서 이러한 값을 찾음으로써 회복될 수 있다.이 자동화에서 상태 쌍을 결합하는 데 사용되는 연산 ×는 직사각형 띠라고 알려진 대수적 구조를 형성한다.[5]

십진수를 2 또는 5로 곱하면 셀당 10개의 상태(십진수 10자리)를 갖는 1차원 가역성 셀룰러 자동화에 의해 수행될 수 있다.제품의 각 자릿수는 동일한 위치에 있는 자리와 오른쪽에 있는 자리 한 자리라는 두 자리 숫자의 주변에만 의존한다.보다 일반적으로 모든 라디ix b에서 역시 주요 요인이 b의 주요 요인이 되는 승수 또는 분수 x에 의한 두 배의 무한 자릿수 시퀀스의 곱이나 나눗셈은 세포 자동화를 형성하는 연산인데, 이는 주변의 한정된 숫자에만 의존하기 때문이며, 곱셈이 존재하기 때문에 되돌릴 수 있다. 역행의[6]다른 값에 의한 곱하기(예: 소수 자릿수를 3으로 곱하기)는 가역성을 유지하지만, 결과에서 한 자릿수를 결정하는 데 필요한 초기 값의 자릿수에 고정된 바운드가 없기 때문에 셀룰러 자동화를 정의하지는 않는다.

되돌릴 수 없는 기본적인 셀룰러 오토마타는 없다.[7]단, 규칙 90 및 기타 기본 셀룰러 오토마타는 독점적 또는 기능에 근거하여 근거리 무선 기능이 제공된다.규칙 90에서 각 셀의 상태는 두 이웃의 배타적 또는 이전 주이다.이러한 전용 또는 전환 규칙을 사용하면 이 규칙에 의해 연속적인 상태 반복이 생성될 수 있다는 점에서 국지적으로 변환 규칙을 되돌릴 수 없다.규칙 90은 되돌릴 수 있는 세포 자동 규칙이 아니다. 왜냐하면 규칙 90에서 모든 상태는 전체 셀 배열에 대한 4개의 가능한 선행 규칙이 있는 반면, 가역 규칙은 구성당 정확히 1개의 선행 규칙이 있어야 하기 때문이다.[8]

크리터스

주요기사 : Critters (세포자동화)
글라이더는 Critters의 중앙 랜덤 시드 영역에서 탈출하여 세포 자동화를 차단한다.

가장 유명한 세포자동화 규칙 중 하나인 콘웨이의 게임 오브 라이프(Game of Life)는 되돌릴 수 없다. 예를 들어, 완전히 소멸되는 많은 패턴을 가지고 있기 때문에 모든 세포가 죽은 구성에는 전임자가 없는 에덴 동산 패턴도 있다.그러나 발명가 토마소 토폴리와 노먼 마골러스가 쓴 또 다른 '크리터스'라는 규칙은 되돌릴 수 있고 라이프와 비슷한 동적 행동을 가지고 있다.[9]

Critters 규칙은 블록 셀룰러 오토매틱으로, 각 단계에서 자동자의 셀을 2×2 블록으로 분할하고 각 블록을 다른 블록과 독립적으로 업데이트하는 블록 셀룰러 오토매틱은 블록 셀룰러 오토매틱이다.그것의 전이 기능은 정확히 두 개의 살아있는 세포가 없는 블록에서 모든 세포의 상태를 뒤집고, 게다가 정확히 세 개의 살아있는 세포로 180° 블록을 회전한다.이 기능은 변환이 불가능하기 때문에, 이 규칙들에 의해 정의된 자동화는 되돌릴 수 있는 세포 자동이다.[9]

죽은 세포의 더 큰 영역 안에서 중심에 있는 더 작은 무작위 세포의 작은 영역으로 시작했을 때, 생명의 글라이더와 유사한 많은 작은 패턴들이 중심 무작위 영역에서 탈출하여 서로 상호작용한다.크래터스 법칙은 또한 무한히 다양한 주기의 오실레이터뿐만 아니라 다양한 속도의 더 복잡한 우주선을 지원할 수 있다.[9]

시공

몇 가지 일반적인 방법은 자동으로 되돌릴 수 있는 세포 자동측정 규칙을 만드는 것으로 알려져 있다.

세포자동차단기

주요 기사:블록 셀룰러 오토매틱
셀룰러 오토마타 블록을 위한 마골러스 동네.셀의 칸막이는 파란색 실선으로 표시된 2×2블록 세트와 빨간색 실선으로 표시된 블록 세트 사이에서 번갈아 나타난다.

블록 셀룰러 오토매틱은 매 단계마다 오토매틱의 셀이 결합 서브셋(블록이라고 함)으로 분할되어 각 블록에 독립적으로 동일한 변환이 적용되는 오토매틱이다.일반적으로 이러한 자동화는 둘 이상의 파티션을 블록으로 사용하고 시스템의 다른 시간 단계에서 이러한 파티션 간에 회전한다.[10]마르골루스 동네라고 불리는 이 디자인의 자주 사용되는 형태에서, 자동화의 세포들은 사각 격자를 형성하고 각 단계에서 더 큰 2 × 2 제곱 블록으로 분할된다.한 번에 블록의 중심은 다음 번에 4블록의 구석이 되고, 반대로 2×2의 각 4개의 셀은 이전 칸막이의 4개의 다른 2×2제곱에 속하게 된다.[11]위에서 논의한 크리터스 규칙은 이러한 유형의 자동화의 예다.

블록 셀룰러 자동화를 위한 가역 규칙을 설계하고, 주어진 규칙이 가역 가능한지 여부를 결정하는 것은 쉽다. 블록 셀룰러 자동화가 가역적이 되려면 자동화의 각 단계에서 개별 블록에 적용되는 변환 자체가 가역적일 필요가 있고 충분하다.블록 셀룰러 자동화가 가역될 때, 그것의 역학관계의 시간역전 버전은 동일한 블록 구조를 가진 블록 셀룰러 자동화로 설명될 수 있으며, 블록으로 분할된 시간역전 시퀀스를 사용하며, 각 블록에 대한 전환 기능이 원래 규칙의 역기능이 된다.[10]

되돌릴 수 없는 자동모사 시뮬레이션

토폴리(1977)는 되돌릴 수 없는 d차원 셀룰러 오토매틱 규칙을 되돌릴 수 있는 (d + 1)차원 규칙에 내장하는 방법을 보여주었다.새로운 되돌릴 수 있는 규칙의 각 d차원 조각은 원래 규칙의 단일 시간 단계를 시뮬레이션한다.이러한 방식으로 토폴리는 임의의 튜링 기계를 시뮬레이션하는 기능과 같이 되돌릴 수 없는 셀룰러 오토마타의 많은 특징들이 또한 되돌릴 수 있는 셀룰러 오토마타까지 확장될 수 있다는 것을 보여주었다.

토폴리의 추측과 허클링(1998)이 증명했듯이, 토폴리의 방법에 의해 야기된 차원 증가는 그 일반성을 위해 필요한 지불이다: 가벼운 가정(내장물의 변환-불변성 등), 에덴동산을 가역성 셀룰러 자동화에 내장하는 셀룰러 자동화의 모든 내장에서는 반드시 dime을 증가시켜야 한다.nsion.

모리타(1995)는 허링턴의 가정에 따르지 않고 차원을 변경하지 않는 또 다른 유형의 시뮬레이션을 설명한다.Morita의 방법은 "quiscent" 또는 "dead" 상태가 있는 모든 되돌릴 수 없는 자동화의 유한 구성을 시뮬레이션할 수 있다. 따라서 셀과 셀의 주변이 모두 정지 상태일 경우 다음 단계에서 셀은 대기 상태를 유지한다.시뮬레이션은 원래의 되돌릴 수 없는 자동화와 동일한 차원의 가역 블록 셀룰러 자동화를 사용한다.시뮬레이션된 자동화의 되돌릴 수 없는 단계에 의해 파괴될 정보는 대신 구성에서 시뮬레이션 자동화의 무한 대기 영역으로 전송된다.이 시뮬레이션은 시뮬레이션된 자동화의 모든 셀을 동시에 업데이트하는 것이 아니라, 한 단계를 시뮬레이션하는 시간이 시뮬레이션되는 구성의 크기에 비례한다.그럼에도 불구하고 시뮬레이션은 모든 셀이 동시에 업데이트되는 것처럼 시뮬레이션된 자동화의 동작을 정확하게 보존한다.이 방법을 사용하면 심지어 1차원 가역성 세포 오토마타도 범용 연산이 가능하다는 것을 보여줄 수 있다.[12]

2차 셀룰러 오토마타

2차 셀룰러 오토매틱에서 시간 t의 셀 상태에 영향을 미치는 과거의 셀
규칙 18 1차원 셀룰러 오토메이션(왼쪽)과 그로부터 파생된 2차 셀룰러 오토메이션(오른쪽)이다.이미지의 각 행에는 시간이 아래로 흐르는 자동화의 구성이 표시된다.
주요 기사:2차 셀룰러 오토매틱

2차 셀룰러 오토매틱 기법은 어떤 셀룰러 오토매틱도 가역형 셀룰러 오토매틱으로 변형시키는 방법인데, 에드워드 프레드킨이 발명하고 여러 저자들이 1984년에 처음 출간했다.[13]이 기법에서, 시간 t에서의 자동 t에서의 각 셀의 상태는 시간 t - 1의 근린과 시간 t - 2의 자체 상태 둘 다의 함수다. 구체적으로는, 자동화의 전환 기능은 시간 t - 1의 각 근린들을 상태 집합의 순열에 매핑한 다음, 그 순열을 시간 t - 2의 상태에 적용한다.자동화의 역역학(reverse dynamics)은 각각의 이웃을 역순열에 매핑하여 같은 방식으로 진행함으로써 계산될 수 있다.[14]

2진수 값 상태(0 또는 1)가 있는 오토마타의 경우, 주에서 가능한 순열은 단 두 개뿐이며, 이는 그 자체가 2진수 값을 갖는 배타적 또는 주(州)로 나타낼 수 있다.이러한 방식으로 기존의 2-값 셀룰러 자동화는 시간 t - 1의 상태에서 기존 자동화의 전환 기능을 사용한 다음 시간 t - 2의 상태와 이들 상태의 배타적 또는 시간 t - 2의 상태를 계산하여 시간 t의 상태를 결정할 수 있다.그러나, 이러한 방식으로 결정된 가역성 세포 자동화의 동작은 그것이 정의된 세포 자동화의 동작과 전혀 유사하지 않을 수 있다.[14]

2차 자동화는 2차 자동화의 연속된 시간 단계부터 기존 셀룰러 자동화의 단일 상태로 상태 쌍을 결합함으로써 전환 기능이 이전 단일 단계에만 의존하는 재래식 셀룰러 자동화로 변환될 수 있다.[14]

보존경관

Patt(1971)가 발견한 1차원 세포자동차는 4개의 연속 세포로 구성된 이웃을 이용한다.이 오토메이션에서는, 세포가 패턴 「0?10」에서 「?" 위치를 차지할 때마다 상태를 뒤집는다. 그러한 두 가지 패턴이 겹칠 수 있는 것은 없으므로, 플립된 셀을 둘러싼 동일한 「경관」이 전이 후에도 계속 존재한다.다음 단계에서는 같은 "?" 위치에 있는 셀이 다시 뒤집혀 원래의 상태로 되돌아간다.따라서 이 자동화는 그 자체의 역이며, 가역성이 있다.Patt는 작은 이웃이 있는 2개의 주 1차원 셀룰러 오토마타에 대한 모든 무차별적인 검색을 수행했다. 이 검색은 이 자동화를 발견하게 했고, 그것이 1차원 2차원 되돌릴 수 있는 셀룰러 오토마톤 중 가장 단순하다는 것을 보여주었다.3셀 이웃을 가진 가역형 2주 오토마타는 없으며, 4셀 이웃을 가진 모든 2주 가역형 오토마타는 팻의 오토매틱에 있는 단순한 변형이다.[15]

Patt의 자동화는 되돌릴 수 있는 셀룰러 자동화를 설계하기 위한 "보존된 풍경" 기법의 한 예로 되돌아 볼 수 있다.이 기법에서 세포의 상태에 대한 변화는 스스로 상태를 바꾸지 않는 이웃들의 패턴에 의해 촉발된다.이와 같이 동일한 패턴의 존재는 시간이 경과한 자동화의 역학 변화를 촉발하는 데 이용될 수 있다.Patt의 자동화는 매우 단순한 역학(모든 구성의 순환 시퀀스는 길이 2를 가진다)을 가지고 있지만, 둘 이상의 트리거링 패턴으로 보존된 동일한 가로경관 기법을 사용하는 오토마타는 보다 복잡한 동작을 할 수 있다.특히 그들은 2차전지 자동화를 시뮬레이션 할 수 있다.[15]

밀러&프레드킨(2005)의 SOLT 모델은 보존된 조경기술의 특별한 사례다.이 모델에서 정수 그리드의 셀은 짝수 부분 집합과 홀수 부분 집합으로 분할된다.각 단계에서 다른 패리티의 주변 셀 구성에 따라 한 패리티의 특정 셀 쌍이 교환된다.이 모델을 사용하는 규칙은 당구공 컴퓨터를 시뮬레이션 할 수도 있고,[16] 여러 가지 다른 속도로 움직이거나 여러 다른 주파수에서 진동할 수 있는 살아있는 세포의 긴 줄을 지원할 수도 있다.[17]

이론

셀룰러 오토메이션은 셀의 배열로 구성되는데, 각각의 셀은 한정된 수의 가능한 상태를 가지며, 인접한 셀의 상태만을 기준으로 모든 셀을 동시에 업데이트하는 규칙도 함께 가지고 있다.셀룰러 자동화의 구성은 자동화의 모든 셀에 상태를 할당하는 것이다; 셀룰러 자동화의 업데이트 규칙은 구성에서 구성까지의 함수를 형성하며, 셀의 업데이트 값은 셀의 일부 유한한 이웃에만 의존하고, 기능은 tr에 따라 불변한다.입력 배열의 회선

이러한 정의와 함께, 세포 자동화는 다음 조건 중 하나를 만족시킬 때 되돌릴 수 있으며, 이 모든 조건들은 수학적으로 서로 동등하다.[18]

  1. 자동화의 모든 구성에는 업데이트 규칙에 의해 자동에 매핑되는 고유한 이전 구성이 있다.
  2. 자동화의 업데이트 규칙은 편향이다. 즉, 일대일 기능이다.
  3. 업데이트 규칙은 주입 함수, 즉 두 구성이 모두 동일한 공통 구성에 매핑되는 두 개의 구성이 없다.이 조건은 업데이트 규칙이 편향적이라는 가정에 의해 명백하게 암시된다.다른 방향에서, 세포 자동화를 위한 에덴동산 정리는 모든 주입 업데이트 규칙이 비주사적이라는 것을 암시한다.[19]
  4. 자동화의 시간 역학은 또 다른 세포 자동화로 설명할 수 있다.이것이 가능하려면 업데이트 규칙이 비굴해야 한다.다른 방향에서 업데이트 규칙이 비주사적인 경우, 그것은 또한 비주사적인 역 함수를 가진다.이 역 함수는 세포 자동 규칙이어야 한다.이 사실의 증거는 커티스-을 사용한다.Hedlund-Lyndon 정리, 구성 공간의 칸토어 위상에 관해서 연속적인 변환-상변함수로서의 세포 자동 규칙의 위상학적 특성화.[20]
  5. 자동화의 업데이트 규칙은 상태 공간과 세포 격자의 번역에 의해 정의된 시프트 동적 시스템의 자동형성이다.즉, Curtis--처럼 교대 지도에 통용되는 동형상이다.헤들런드-린든 정리가 함축하고 있다.[21]

Di Gregorio & Trautteur(1975)는 세포 자동화에 대한 가역성의 몇 가지 대체 정의를 분석한다.이들 중 대부분은 주입성 또는 자동화의 전환 기능의 허탈성과 동등한 것으로 판명되지만, 이 두 가지 정의 중 어느 하나와 일치하지 않는 대안이 하나 더 있다.그것은 정지 상태나 정지 상태를 가진 생명의 게임과 같은 오토마타에 적용된다.그러한 자동에서, 미세하게 많은 비쿼시 셀만 가지고 있는 경우, 구성을 "완료"로 정의할 수 있으며, 모든 유한한 구성이 최소한 하나의 유한한 전임자를 갖는 자동타 클래스를 고려할 수 있다.이 세분류는 허탈형 및 주입형 자동자와 구별되는 것으로 밝혀졌으며, 일부 후속 연구에서는 이 특성을 가진 자동자를 변위성 유한 자동자라 불렀다.[22]

가역성 테스트

주어진 1차원 셀룰러 오토매틱의 가역성을 시험하는 문제가 알고리즘 솔루션을 가지고 있다는 것은 아모로소&패트(1972)에 의해 처음 나타났다.오토마타 이론과 드 브루이즌 그래프에 기초한 대체 알고리즘은 컬릭(1987년)과 서트너(1991년)가 각각 부여했다.

  • 컬릭은 전환 기능이 주기적인 구성의 하위 집합(양방향에서 동일한 하위 문자열을 무한정 반복하는 경우)에 주입되는 경우에만 세포 자동이 주입 전환 기능을 가지고 있다는 관찰에서 시작한다.그는 주기적인 문자열에서 자동화의 전환 규칙을 수행하는 비계수적 유한 상태 변환기를 정의한다.이 변환기는 문자열의 시작 부분에 있는 자동화의 주변을 기억하고 입력 끝에 연결된 인접 영역이 비결정적으로 선택된 전환이 정확할 때 합격 상태로 들어가면서 작동한다.그리고 나서 Culik은 변환기의 입력과 출력을 교환한다.이 스왑에서 발생하는 변환기는 주어진 자동화의 역역학을 시뮬레이션한다.마지막으로, Culik은 이전에 알려진 알고리즘을 적용하여 결과적으로 교환된 변환기가 각 입력을 단일 출력에 매핑하는지 여부를 시험한다.[23]
  • Sutner는 각 꼭지점이 연속적인 셀 순서에서 셀에 대한 상태 할당 쌍을 나타내는 지시 그래프(de Bruijn 그래프의 일종)를 정의한다.이 시퀀스의 길이는 오토매틱의 주변 크기보다 한 개 적은 값으로 선택된다.수트너의 그래프의 가장자리는 한 셀을 제외한 모든 셀에서 겹치는 셀의 한 쌍을 나타내며, 따라서 시퀀스의 결합은 셀룰러 자동화의 완전한 이웃이다.그러한 각 가장자리는 왼쪽의 중첩에서 오른쪽의 중첩으로 방향을 정한다.가장자리는 셀 시퀀스의 겹치는 부분에서 호환 가능한 상태 할당을 나타낼 때만 그래프에 포함되며, 자동 규칙(전위 가장자리로 결정된 주변 환경에 적용)이 두 상태 할당에 대해 동일한 결과를 제공할 때만 그래프에 포함된다.이 그래프의 선형 시간 강한 연결 분석을 수행함으로써, 어떤 정점이 사이클에 속하는지 결정할 수 있다.이 그래프가 적어도 하나의 꼭지점에 서로 다른 두 개의 상태 할당이 있는 방향 사이클을 포함하는 경우에만 전환 규칙은 비주관적이다.[8]

이러한 방법들은 입력 자동화의 상태 전환 테이블 크기의 제곱에 비례하는 다항식 시간을 필요로 한다.[24]힐만(1991)의 관련 알고리즘은 주기적인 경계 조건을 가진 셀의 유한 길이 배열에 적용될 때 주어진 규칙이 무시무시한지, 그리고 만약 그렇다면, 어떤 길이에 해당하는지를 결정한다.

블록 셀룰러 자동화의 경우, 시험 가역성 또한 쉽다: 자동화의 블록에 있는 전환 기능이 변환할 수 없는 경우에만 자동화가 역전될 수 있으며, 이 경우 역방향 자동화는 역전환 함수와 동일한 블록 구조를 가지고 있다.[10]

단, 2개 이상의 차원으로 다른 이웃이 있는 셀룰러 오토마타의 경우 가역성 테스트의 문제는 판독할 수 없으며, 이는 항상 문제를 중지하고 항상 정확하게 답하는 알고리즘이 존재할 수 없다는 것을 의미한다.카리에 의한 이러한 사실의 증거는 왕 타일에 의한 평면의 타일링에 대해 이전에 알려진 불분명함에 근거한 것으로, 가장자리에 어떤 타일 쌍이 가장자리에 맞는지 구속하는 네모난 타일 세트 이다.카리는 왕 타일 세트에서 셀룰러 자동화를 정의하는데, 주어진 타일 세트가 전체 평면 타일을 타일로 할 수 있는 경우에만 자동이 주입되지 않는다.그의 건축은 폰 노이만(Von Neumann) 인근과 주(州)가 많은 세포를 사용한다.같은 논문에서, 카리는 또한 2차원 이상의 주어진 세포 자동 법칙이 (즉, 에덴 동산이 있는지) 허탈적인지 시험하는 것은 불찰할 수 없는 것임을 보여주었다.

역주변크기

셀의 근방이 m 셀의 간격인 셀당 n개의 상태를 갖는 1차원 반전성 셀룰러 오토매틱에서 역역학을 나타내는 오토매틱은 최대 nm − 1 - m + 1개의 셀로 구성된 이웃을 가지고 있다.이 경계는 m = 2에 빡빡한 것으로 알려져 있다: 시간 경과 역학 관계가 정확히 n - 1 크기의 셀룰러 자동화를 이루는 2-셀 이웃이 있는 n-state 가역형 셀룰러 오토마타가 존재한다.[25]

어떤 정수 m의 경우 폰 노이만 근방에 있는 2차원 가역형 m-상태 세포자동차가 미세하게 많을 뿐이다.따라서, 폰 노이만 근린과 m-상태 셀룰러 오토마타의 모든 역전은 최대 f(m)의 반경을 가진 근린 지역을 사용하게 하는 잘 정의된 기능 f(m)가 있다: 단순히 f(m)를 시간의 역전을 나타내는 데 필요한 많은 가역형 m-상태 셀룰러 오토마타 중에서 최대값으로 한다.ics of the automaton.그러나 Kari의 불분명한 결과 때문에 f(m)를 계산하는 알고리즘이 없으며 이 함수의 값은 어떤 계산 가능한 함수보다 매우 빠르게, 매우 빠르게 커져야 한다.[12]

울프람의 분류

스테판 울프람에 의해 잘 알려진 세포 자동 분류는 무작위 초기 조건에서 그들의 행동을 연구한다.가역형 셀룰러 자동화의 경우, 가능한 모든 구성 중에서 초기 구성을 균일하게 무작위로 선택한 경우, 동일한 균일한 무작위성이 모든 후속 상태에 대해 계속 유지된다.따라서 대부분의 가역성 세포 자동화는 울프램의 등급 3: 거의 모든 초기 구성이 사이비 무작위 또는 과장되게 진화하는 오토마타인 것처럼 보일 것이다.그러나, 국소적 동요가 자동화의 거동에 미치는 영향을 분석함으로써 서로 다른 가역적 세포 자동화를 구별할 수 있다.가역성 세포 자동화의 초기 상태를 변경하면 이후 상태에 대한 변화가 경계가 있는 지역 내에서만 유지되거나 불규칙하지만 무한히 전파되거나 빠르게 확산될 수 있으며, 울프람(1984)은 이러한 세 가지 유형의 행동을 모두 보여주는 1차원 가역성 세포 자동화 규칙을 나열한다.

울프람의 후기 연구는 1차원 규칙 37R 자동화가 이 점에서 특히 흥미롭다고 본다.더 큰 빈 동네를 중심으로 한 작은 무작위 세포의 씨앗에서 시작하여 주기적인 경계 조건을 가진 유한한 배열의 세포에서 달리면, 질서와 혼돈 상태 사이에서 요동치는 경향이 있다.그러나, 무한의 셀 집합에서 동일한 초기 조건과 함께 그것의 구성은 몇 가지 유형의 단순한 이동 입자로 구성되는 경향이 있다.[26]

추상대수학

되돌릴 수 있는 세포 자동화를 공식화하는 또 다른 방법은 추상 대수학을 포함하며, 이러한 공식화는 가역 가능한 세포 자동화에 대한 컴퓨터 검색을 개발하는 데 유용했다.보이케트(2004)는 반원소 빅그룹을 원소 쌍에 대해 설정된 S와 두 개의 연산 → 및 ←로 구성된 대수적 구조로 정의하여 두 개의 등가 공리를 만족한다.

  • S의 모든 원소 a, b, c에 대해, (a → b) ( (b → c) = b.
  • S의 모든 원소 a, b, c에 대해, (a b b) → (b ← c) = b.

예를 들어, 운영 → 오른쪽 인수, 운영 ← 왼쪽 인수를 반환하는 두 운영의 경우 그렇다.

보이켓의 주장대로, 어떤 1차원 가역성 세포 자동화는 직사각형 형태의 자동화와 동등하다. 직사각형 형태에서는 세포가 매 단계마다 반 단위를 상쇄하고, 자동화의 전진 및 역진화 모두 단지 두 개의 세포로 이웃을 가지고 있는데, 그 세포는 각 방향으로 반 단위 떨어져 있다.가역형 자동화가 2개 이상의 셀을 가진 경우, 시뮬레이션 자동화의 각 셀이 시뮬레이션 자동화의 연속된 셀 블록을 시뮬레이션하는 셀당 더 많은 셀과 더 작은 이웃을 가진 가역형 자동화에 의해 시뮬레이션될 수 있다.반원형 거대집단의 두 공리는 정확히 이들 두 개의 셀 동네의 전진 및 후진 전환 기능이 서로 역행하는 데 필요한 조건이다.즉, 모든 반원형 빅그룹노이드는 직사각형 형태로 가역성 세포 자동화를 정의하는데, 여기서 자동화의 전환 기능은 → 연산을 사용하여 근방의 두 개의 셀을 결합하고, operation 연산은 비슷하게 자동화의 역역학을 정의한다.모든 1차원 가역성 세포 자동화는 이 형태에서 한 개와 같다.[5]

보이켓은 이 대수적 공식화를 모든 가능한 불평등 가역성 세포 자동자를 완전히 나열하는 알고리즘의 기초로 사용했다.[27]

보존법

연구자들이 물리적 시스템을 시뮬레이션하기 위해 가역성 셀룰라 오토마타를 설계할 때, 그들은 일반적으로 시스템의 보존 법칙을 설계에 통합한다. 예를 들어, 이상적인 가스를 시뮬레이션하는 셀룰러 자동화는 가스 입자의 수와 그것의 총 모멘텀을 보존해야 한다. 그렇지 않으면 정확한 모멘텀을 제공하지 못할 것이기 때문이다.그러나, 어떤 의도적인 설계와는 무관하게, 되돌릴 수 있는 세포 자동화가 가질 수 있는 보존 법칙에 대한 연구도 있었다.이러한 연구에서 측정한 보존량의 전형적 유형은 자동화된 k세포의 모든 연속적인 하위 집합에 걸쳐 각 하위 집합에 있는 세포 상태의 일부 수치 함수의 합을 취한다.그러한 양은 한정된 값을 취할 때마다 자동화의 각 단계마다 그 값이 자동으로 일정하게 유지되고, 이 경우 자동화의 kth-order 불변량이라고 불린다면 보존된다.[28]

예를 들어, 셀 상태가 왼쪽 값과 오른쪽 값의 집합 L과 R에서 도출된 값(l,r)의 쌍이며, 각 셀의 왼쪽 값이 각 단계마다 오른쪽으로 이동하고, 각 셀의 오른쪽 값이 왼쪽으로 움직이는 직사각형 대역의 예로서 정의된 1차원 셀룰러 자동을 떠올려 보자.이 경우 밴드의 각 왼쪽 또는 오른쪽 값 x에 대해 보존된 수량, 즉 해당 값을 갖는 총 셀 수를 정의할 수 있다.만일 left 왼쪽 값과 ρ 오른쪽 값이 있다면 λ + ρ - 2 독립 1차 변이체가 있으며, 어떤 1차 변이체도 이러한 기본 변이들의 선형 결합으로 나타낼 수 있다.왼쪽 값과 연관된 보존 수량은 일정한 비율로 오른쪽으로 균일하게 흐른다. 즉, 라인의 일부 지역 C 내에서 x와 같은 왼쪽 값의 수가 0시에 일정한 값을 갖는 경우, t에서 이동된 지역 C + t/2에 대해 동일한 값을 취한다.마찬가지로, 올바른 값과 관련된 보존 수량은 왼쪽으로 균일하게 흐른다.[29]

1차원 가역형 셀룰러 자동은 직사각형 형태로 배치될 수 있으며, 그 후에 전환 규칙이 상태 집합의 순열과 함께 idempotent 반원형 빅그룹(단일한 상태 값을 가진 셀 영역이 경계에서만 변하는 가역형 규칙)의 작용에 반영될 수 있다.자동규칙(허용을 생략하여 형성된 변형된 규칙)의 idempotent 리프팅을 위한 1차 불변제는 반드시 직사각형 밴드의 그것과 같이 동작한다. 그들은 상호 작용 없이 일정한 속도로 왼쪽이나 오른쪽으로 흐르는 불변성의 기초를 가지고 있다.전체 자동화를 위한 1차 불변제는 정확히 순열의 동일한 궤도에 속하는 모든 상태 쌍에 동일한 중량을 주는 공회전제 리프팅의 불변성이다.그러나 규칙에서 상태의 순열은 이러한 불변성이 불균일하게 흐르며 상호작용을 동반하는 idempotent 리프팅에서와 다르게 행동하게 할 수 있다.[29]

물리적 시스템에서 노에더의 정리는 보존 법칙과 시스템의 대칭 사이에 동등성을 제공한다.그러나, 세포 자동화의 경우, 시스템의 에너지에 의해 지배되는 대신, 자동화의 동작은 그 규칙으로 암호화되고, 자동화는 그것이 따를 수 있는 어떤 보존법칙에 관계없이 특정한 대칭(공간과 시간의 변환 불변성)을 준수하도록 보장되기 때문에, 이 정리가 직접적으로 적용되지는 않는다.그럼에도 불구하고, 특정 가역성 시스템의 보존량은 어떤 면에서 에너지와 유사하게 작용한다.예를 들어, 자동화의 지역마다 보존된 수량의 평균값이 다를 경우, 자동화의 규칙은 이 수량이 소멸되어 이후 상태에서는 수량의 분포가 더 균일해질 수 있다.이러한 보존된 양을 시스템의 에너지에 대한 스탠드로 사용하면 고전 물리학의 방법을 사용하여 분석할 수 있다.[30]

적용들

격자 가스 오토마타

주요기사 : 격자가스자동화

격자 가스 자동화는 유체나 이상적인 기체에서 입자의 움직임을 시뮬레이션하도록 설계된 세포 자동이다.그러한 시스템에서는 가스 입자가 다른 입자와 탄성 충돌을 겪을 때까지 일정한 속도로 직선으로 움직인다.격자 가스 오토마타는 일정한 수의 속도(일반적으로 1개의 속도 및 4~6개의 방향 중 하나)만 허용하고 가능한 충돌 유형을 단순화하여 이러한 모델을 단순화한다.[31]

구체적으로 HPP 격자 가스 모델은 4축 평행 방향에서 단위 속도로 이동하는 입자로 구성된다.두 입자가 반대 방향으로 같은 선에서 만나면 충돌하여 수직선의 충돌 지점에서 바깥쪽으로 보내진다.이 시스템은 물리적 가스의 보존 법칙을 준수하며, 물리적 가스의 행동과 유사한 외관을 가진 시뮬레이션을 생성한다.그러나 비현실적인 추가 보존법을 준수하는 것으로 밝혀졌다.예를 들어, 어떤 단일 라인 내의 총 모멘텀은 보존된다.또한 이 모델에서 축-병렬 방향과 비축-병렬 방향 사이의 차이(이소트로피)는 바람직하지 않을 정도로 높다.FHP 격자 가스 모델은 입자가 4개 방향만이 아닌 60도 각도로 서로 다른 6개 방향으로 이동하도록 하여 HPP 모델을 개선한다.어떤 정면 충돌에서도, 두 개의 나가는 입자는 두 개의 들어오는 입자로부터 60도 각도로 꺾인다.3방향 충돌은 FHP 모델에서도 가능하며, 총 운동량을 보존하고 HPP 모델의 비물리적 부가 보존 법칙을 피하는 방식으로 처리된다.[31]

이 시스템들에서 입자의 움직임은 가역성이 있기 때문에, 그것들은 전형적으로 가역성 세포 자동화와 함께 구현된다.특히 HPP와 FHP 격자 가스 오토마타 모두 마르골루스 인근을 이용한 2주 블록 셀룰러 오토매틱으로 구현이 가능하다.[31]

이싱 모형

Ising 모델은 자기계통의 행동을 모델링하는데 사용된다.그것은 위아래로 스핀을 나타내는 각각의 상태를 나타내는 셀의 배열로 구성되어 있다.계통의 에너지는 서로 같은 스핀을 갖는 인접한 셀 쌍의 수에 따라 달라지는 함수에 의해 측정된다.따라서, 만약 어떤 세포가 두 주에서 동일한 수의 이웃을 가지고 있다면, 그것은 전체 에너지를 바꾸지 않고 그 자신의 상태를 뒤집을 수 있다.그러나 이러한 플립은 인접한 두 셀이 동시에 플립하지 않는 경우에만 에너지를 절약할 수 있다.[32]

이 시스템의 셀룰러 자동 모델은 사각 격자를 두 개의 교대 서브셋으로 나누고, 한 번에 두 서브셋 중 하나를 업데이트한다.각각의 업데이트에서 뒤집힐 수 있는 모든 셀은 그렇게 한다.이것은 Ising 모델을 조사하는 데 사용할 수 있는 가역성 세포 자동화를 정의한다.[32]

당구공 계산 및 저전력 컴퓨팅

프레드킨&토폴리(1982)는 이 당구공 컴퓨터를 가역 컴퓨팅에 대한 조사의 일환으로 제안했다.당구공 컴퓨터는 트랙에서 움직이는 동기화된 입자(당구공)의 시스템으로 구성되며 고정된 장애물에 의해 유도된다.입자들이 서로 충돌하거나 장애물과 충돌할 때, 그들은 실제 당구공처럼 탄력적인 충돌을 겪는다.컴퓨터에 대한 입력은 특정 입력 트랙의 입자의 유무에 따라 암호화되며, 출력 트랙의 미립자 유무에 따라 출력도 유사하게 인코딩된다.선로 자체는 전선으로, 입자는 전선으로 전송되는 부울 신호로 상상될 수 있다.입자가 장애물에 부딪히면, 그것은 장애물로부터 반사된다.이러한 반사는 입자가 따르고 있는 전선 방향의 변화로 해석될 수 있다.서로 다른 트랙에 있는 두 개의 입자가 충돌할 수 있으며, 충돌 지점에서 논리 게이트를 형성할 수 있다.[33]

Margolus(1984)가 보여주었듯이 당구공 컴퓨터는 Margolus 이웃과 함께 2개의 상태 가역 블록 셀룰러 자동화를 사용하여 시뮬레이션할 수 있다.이 자동화의 업데이트 규칙에서, 정확히 하나의 라이브 셀이 있는 블록은 180° 회전하고, 대각선 방향으로 두 개의 라이브 셀이 있는 블록은 90° 회전하며, 다른 모든 블록은 변경되지 않은 상태로 유지된다.이 규칙들은 고립된 살아있는 세포들이 대각선 궤도를 따라 움직이면서 당구공처럼 행동하게 한다.하나 이상의 살아있는 세포로 구성된 연결된 그룹은 대신 당구공 컴퓨터의 고정 장애물처럼 행동한다.마골러스는 또한 부록에서 2차원 무어 지역을 사용하는 3주 2차 셀룰러 오토매틱이 당구공 컴퓨터를 시뮬레이션할 수 있다는 것을 보여주었다.

수학의 미해결 문제:

모든 3차원 가역형 셀룰러 자동화가 국소적으로 가역 가능한가?

(수학에서 더 풀리지 않은 문제)

당구공 모델과 같이 되돌릴 수 있는 보편적인 연산 모델을 연구해야 하는 한 가지 이유는 이론적으로 매우 적은 양의 에너지를 소비하는 실제 컴퓨터 시스템으로 이어질 수 있기 때문이다.랜다워의 원리에 따르면 되돌릴 수 없는 계산 단계는 단계당 일정한 최소한의 에너지가 필요하지만, 가역 가능한 단계는 임의로 0에 가까운 단계당 에너지의 양으로 수행할 수 있다.[34]그러나, 랜다워의 바운드보다 적은 에너지를 사용하여 연산을 수행하기 위해서는 세포 자동이 세계적으로 가역할 수 있는 전환 기능을 갖는 것이 충분하지 않다. 필요한 것은 전환 기능의 로컬 연산도 가역적인 방법으로 행해지는 것이다.예를 들어, 가역 블록 셀룰러 오토마타는 항상 국소적으로 가역할 수 있다: 각 개별 블록의 동작은 미세하게 많은 입력과 출력으로 가역할 수 있는 기능의 적용을 수반한다.토폴리와 마골러스(1990년)는 모든 가역성 세포 자동화에 로컬로 가역성 업데이트 규칙이 있는지 처음으로 물었다.카리(1996)는 1차원 및 2차원 자동자의 경우 양성 반응이 나왔고, 듀란드로스(2001)는 가역형 셀룰러 자동화가 국소적으로 (아마도 다른) 가역형 셀룰러 자동화에 의해 시뮬레이션될 수 있다는 것을 보여주었다.그러나 모든 가역적 전환 기능이 국소적으로 가역적인가 하는 문제는 2개 이상의 차원에 대해서는 여전히 열려 있다.[35]

동기화

Tron 규칙에 의해 생성된 직선 모양

토폴리와 마르골루스의 트론(Tron) 법칙은 마르골루스 이웃과 함께 되돌릴 수 있는 블록 세포 법칙이다.2 × 2 블록의 셀이 모두 동일한 상태를 가질 때, 블록의 모든 셀은 상태가 변한다. 다른 모든 경우, 블록의 셀은 변하지 않는다.토폴리와 마르골루스가 주장하듯이, 이 규칙에 의해 생성되는 패턴의 진화는 마르골루스 동네의 어떤 다른 규칙도 동기화하는 시계로 사용될 수 있다.이와 같이 동기화된 세포자동차는 비동기 세포자동으로 실행하면서 표준 마골루스 근린생활 규칙과 동일한 역학관계를 준수한다.[36]

암호화

카리(1990년)는 암호화 시스템으로 다차원 가역성 셀룰러 오토마타를 사용할 것을 제안했다.카리의 제안에서는 세포 자동 법칙이 암호키가 될 것이다.암호화는 규칙을 한 단계 앞으로 실행하여 수행되고 암호 해독은 한 단계 뒤로 실행되어 수행된다.카리는 이와 같은 시스템을 공개키 암호 시스템으로 사용할 수 있다고 제안한다.원칙적으로 공격자는 가역성 시험의 불해독성 때문에 주어진 암호화 키(전방 규칙)로부터 암호 해독 키(역방향 규칙)를 알고리즘적으로 결정할 수 없었으므로, 시스템의 보안을 훼손하지 않고 포워드 규칙을 공개할 수 있었다.그러나, Kari는 그러한 시스템에 어떤 유형의 가역성 셀룰러 자동화를 사용해야 하는지 명시하거나, 이 접근방식을 사용하는 암호 시스템이 어떻게 암호화/암호 해독 키 쌍을 생성할 수 있는지를 보여주지 않았다.

차이, 차오, 저우(2005)는 대체 암호화 시스템을 제안했다.그들의 시스템에서 암호화 키는 1차원 셀룰러 자동화의 각 셀에 대한 로컬 규칙을 결정한다.이 규칙에 기반한 2차 자동화는 암호화된 출력으로 변환하기 위해 입력에 대해 여러 라운드에 걸쳐 실행된다.자동화의 가역성 속성은 동일한 시스템을 역방향으로 실행하여 암호화된 메시지의 암호를 해독할 수 있도록 한다.이 시스템에서는 암호화와 암호 해독에 모두 동일한 키가 사용되기 때문에 키를 비밀에 부쳐야 한다.

양자 컴퓨팅

주요 기사:양자세포자동화

양자 세포 자동자는 상태와 상태 전환이 양자 역학의 법칙을 따르는 자동자 배열이다.양자 세포 오토마타는 파인만(1982년)에 의해 연산 모델로 제안되었고 와트로닉(1995년)에 의해 처음으로 공식화되었다.이러한 자동화에 대한 몇 가지 경쟁적 개념은 연구 중에 있으며, 그 중 많은 개념은 이러한 방식으로 건설된 자동화를 되돌릴 수 있어야 한다.[37]

물리적 보편성

얀징(2010)은 세포 자동화가 물리적으로 보편화될 수 있는지 질문했는데, 이는 즉, 자동 세포의 경계 영역에 대해, 상태가 적절한 지지 비계를 형성하는 세포로 그 지역을 둘러싸서 자동화가 일련의 임의 변환을 실행하도록 하는 것이 가능해야 한다는 것을 의미한다.지역 내의 주이 성질이 없는 오토마타는 에덴동산 패턴을 가지고 있고, 에덴동산을 만드는 변혁을 구현할 수 없기 때문에 이러한 자동화는 되돌릴 수 있거나 적어도 국소적으로 주입되어야 한다.

샤이퍼(2015년)는 이러한 의미에서 물리적으로 보편적인 가역성 세포 자동화를 구축했다.셰퍼의 오토매틱은 두 개의 주와 마골리스 근방이 있는 블록 셀룰러 오토매틱으로 당구공 모델과 HPP 격자 가스의 오토마타와 밀접한 관련이 있다.그러나 당구공 모델은 일부 지역 내 국가가 읽고 변형되는 것을 막는 뚫을 수 없는 벽을 쌓는 데 사용될 수 있기 때문에 물리적으로 보편적인 것은 아니다.셰퍼의 모델에서 모든 패턴은 결국 4방향으로 대각선으로 움직이는 입자로 분해된다.따라서 그의 오토매틱은 튜링의 완전한 것이 아니다.그러나 셰퍼는 그것보다 더 천천히 분해되는 비계에 의해 어떤 유한한 구성을 둘러싸는 것이 가능하다는 것을 보여주었다.구성이 입자로 분해된 후, 비계는 그러한 입자들을 가로채서 비계 내에 구성된 부울 회로 시스템에 대한 입력으로 사용한다.이러한 회로는 초기 구성의 임의 기능을 계산하는 데 사용할 수 있다.그런 다음 비계는 회로의 출력을 다시 움직이는 입자의 시스템으로 변환하여 초기 영역에 수렴하여 서로 충돌하여 변환된 상태의 복사본을 만든다.이런 식으로 셰퍼의 시스템은 어떤 기능도 주 공간의 어떤 경계 영역에 적용하는 데 사용할 수 있으며, 이 자동 법칙이 물리적으로 보편적이라는 것을 보여준다.[38]

메모들

  1. ^ 울프람(2002년), 페이지 1018.
  2. ^ 쉬프(2008), 페이지 44.
  3. ^ 토폴리 & 마골루스(1990).
  4. ^ 블랜차드, 데바니 & 킨(2004) 페이지 38: "시프트 맵은 상징 역학에서 의심할 여지 없이 근본적인 물체다."
  5. ^ a b 보이케트(2004)
  6. ^ 울프람(2002년), 페이지 1093.
  7. ^ 패트(1971년).
  8. ^ a b 수트너(1991년).
  9. ^ a b c 토폴리 & 마골루스(1987), 섹션 12.8.2, "비평가들", 페이지 132–134; 마골루스(1999), 마로타(2005).
  10. ^ a b c 토폴리와 마골루스(1987), 섹션 14.5, "파티션화 기법", 페이지 150–153; 쉬프(2008), 섹션 4.2.1, "파티션 셀룰러 오토마타", 페이지 115–116.
  11. ^ 토폴리 & 마골루스(1987), 12장 "마골루스 이웃" 페이지 119–138.
  12. ^ a b 카리(2005년).
  13. ^ 마르골루스(1984년), 비히니악(1984년), 울프람(1984년).
  14. ^ a b c 토폴리 & 마골루스(1987), 섹션 14.2, "2차 주문 기법", 페이지 147–149.울프람(2002년), 페이지 437ff.매킨토시(2009년).
  15. ^ a b 토폴리 & 마골루스(1990), 섹션 5.3, "보존경관 순열", 페이지 237–238.
  16. ^ 밀러 & 프레드킨(2005년).
  17. ^ 밀러 & 프레드킨(2012년).
  18. ^ 1차원 사례에서, 이러한 동등성들 중 몇몇은 이미 세포 자동화가 아닌 역동적인 시스템의 언어로 Hedlund(1969년), Organy 4.1에 의해 제시되었다.더 높은 치수는 리처드슨(1972)과 디 그레고리오 & 트라우트터(1975)를 참조한다.
  19. ^ 마이힐(1963년).
  20. ^ 리처드슨(1972년).
  21. ^ 헤들런드(1969년).
  22. ^ 모라알(2000년)
  23. ^ 컬릭은 이 결과에 대해 1979년 오토마타 이론 교과서를 인용하지만, 베알 외 연구 자료를 참조한다. (2003) 변환기가 함수를 정의하는지 여부를 효율적으로 시험하기 위한 최신 개발.
  24. ^ 아모로소&패트(1972)나 컬릭(1987) 모두 알고리즘의 시간 복잡성을 명시적으로 진술하지 않지만, 수트너(1991)는 그렇게 하고, 이 바운드는 체이즐러&카리(2007)에서도 찾아볼 수 있다.
  25. ^ 카리(1992년), 체이즐러(2004년), 체이즐러&카리(2007년).
  26. ^ 울프람(2002년), 페이지 454–457.
  27. ^ 보이케트(2004)힐만(1991)과 젝 투오 모라 외 연구소를 참조한다. (2005) 폭-2 가역성 셀룰러 오토마타의 열거에 관한 밀접하게 관련된 연구를 위한 것이다.
  28. ^ 핫토리&타케슈(1991);후쿠치(2007년).
  29. ^ a b 보이켓, 카리 & 타아티(2008).
  30. ^ Pomau(1984년), Takesue(1990년), Capobianco & Tofoli(2011년).
  31. ^ a b c 토폴리 & 마골루스(1987), 16장 "유체 역학", 페이지 172–184.
  32. ^ a b 토폴리 & 마르골루스(1987), 17.2장 "이싱 시스템" 페이지 186–190.
  33. ^ 듀란드로스(2002년).
  34. ^ 프레드킨&토폴리(1982년).
  35. ^ 카리 (2005, 2009)
  36. ^ 토폴리 & 마골루스(1987), 섹션 12.8.3, "비동기식 연산", 페이지 134–136.
  37. ^ 마이어(1996); 슈마허&베르너(2004);셰퍼드, 프란츠 & 베르너(2006);나가즈 & 보잔(2008).
  38. ^ 2014년 6월 26일 "A Physical Universal Cellular Automaton", Shtetl-Optimized, Scott Aaronson을 참조하십시오.

참조