룽지 현상

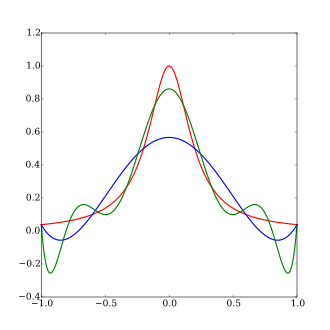
수치해석의 수학적 분야에서 룬지 현상(Runge's phenomeness) 독일어:[ˈʁʊŋə])는 등간격 보간 점들의 집합에 걸쳐 고도의 다항식들과 함께 다항식 보간을 사용할 때 발생하는 간격의 가장자리들에서의 진동 문제입니다. 칼 데이비드 톨메 룬지(Carl David Tolmé Runge, 1901)는 특정 함수를 근사화하기 위해 다항식 보간법을 사용할 때 오류의 거동을 탐구할 때 발견했습니다.^[1] 이 발견은 더 높은 곳으로 가는 것이 항상 정확도를 향상시키는 것은 아니라는 것을 보여줍니다. 이 현상은 푸리에 급수 근사치의 깁스 현상과 유사합니다.

서론

Weierstrass 근사 정리는 [a,b] 구간에 정의된 모든 연속 함수 f(x)에 대하여, n=0, 1, 2, …에 대한 다항 함수 P(x)의 집합이 존재하며, 각각의 차수는 n이 무한대인 경향이 있으므로 [a,b]에 대해 균일한 수렴을 갖는 f(x)에 근사한다고 말합니다. 즉,

${\displaystyle \lim_{n\rightarrow \infty}\left(\sup_{a\leq x\leq b}\left f(x)-P_{n}(x)\right \right)=0.}$

이 점들을 통과하는 n차 다항식 P(x_n)를 사용하여 함수 f(x)의 n+1개의 등간격 점을 보간하려는 경우를 생각해 보자. 당연히 더 많은 점을 사용하면 f(x)를 더 정확하게 재구성할 수 있다고 Weierstrass의 정리에서 기대할 수 있습니다. 그러나 이 특정 다항 함수 집합_n P(x)는 균일한 수렴의 속성을 갖는 것이 보장되지 않습니다. 이 정리는 다항 함수 집합이 존재한다는 것만 언급하고, 하나를 찾는 일반적인 방법을 제공하지 않습니다.

이렇게 생성된 P_n(x)는 실제로 n이 증가함에 따라 f(x)로부터 멀어질 수 있으며, 이는 일반적으로 보간 포인트의 끝 근처에서 확대되는 발진 패턴에서 발생합니다. 이 현상의 발견은 룬지 덕분입니다.^[2]

문제

룬지 함수를 고려합니다.

${\displaystyle f(x)={\frac {1}{1+25x^{2}}}\,}$

('아그네시의 마녀'의 축척된 버전) 룬지는 이 함수를 -1과 1 사이의 등거리점 x에서_i 보간하면 다음과 같은 결과를 얻을 수 있습니다.

${\displaystyle x_{i}={\frac {2i}{n}-1,\quad i\in \left\{0,1,\dots,n\right\}$

차수가 ≤ n인 다항식_n P(x)인 경우, 결과적인 보간은 구간의 끝, 즉 -1과 1에 가까운 방향으로 진동합니다. 다항식의 차수가 증가할 때 보간 오차가 증가한다는 것이 (경계 없이) 증명될 수도 있습니다.

${\displaystyle \lim_{n\rightarrow \infty}\left(\sup_{-1\leq x\leq 1} f(x)-P_{n}(x) \right)=\infty.}$

이는 등거리 지점에서 고차 다항식 보간이 번거로울 수 있음을 보여줍니다.

이유

룽지 현상은 이 문제의 두 가지 속성의 결과입니다.

• 이 특정 함수의 n차 도함수의 크기는 n이 증가할 때 빠르게 증가합니다.
• 점 사이의 등거리는 n이 증가할 때 빠르게 증가하는 르베그 상수로 이어집니다.

두 특성이 결합하여 진동의 크기를 증가시키기 때문에 이 현상은 그래픽적으로 분명합니다.

생성 함수와 n차의 보간 다항식 사이의 오차는 다음과 같이 주어집니다.

${\displaystyle f(x)-P_{n}(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}\prod _{i=0}^{n}(x-x_{i})}$

(-1, 1)의 $일부$ξ에 대해 ${\displaystyle$ \xi$}.$ 따라서,

${\displaystyle \max _{-1\leq x\leq 1} f(x)-P_{n}(x) \leq \max _{-1\leq x\leq 1}{\frac {\left f^{(n+1)}(x)\right }{(n+1)!$$}}\max _{-1\leq x\leq 1}\prod _{i=0}^{n} x-x_{i} }$.

${\displaystyle n_{}}$${\displaystyle {}_{}x)}$ ${\displaystyle w_{n}(x)}$ 결절 함수로 표시합니다.

${\displaystyle w_{n}(x)=(x-x_{0})(x-x_{1})\cdots (x-x_{n})}$

${\displaystyle {그리고}_{}}$ W ${\$를 ${\displaystyle W_{}}$ ${\$ 함수의$$ 최대 크기로$$ 설정합니다.

${\displaystyle {}_{}{W}_{}}$ = ${\displaystyle \underset{}{max}}$- $1$≤ x ≤ 1 w (x) {\displaystyle W${\displaystyle {\_}_{}}${n} =\max _{-1\leq x\leq 1} w_{n}(x) }.

등거리 노드를 사용하여 다음을 증명하는 것은 기본적입니다.

${\displaystyle W_{n}\leq n!h^{n+1}}$

여기서 $h$ = ${\displaystyle 2}$/ n {\displaystyle h = 2/n}은 스텝 크기입니다.

또한 $f{\displaystyle }$ ${\displaystyle f}$의 (n+1)번째 도함수가 유계라고$$ 가정합니다.

${\displaystyle \underset{}{max}}$- ${\displaystyle \underset{}{1}}$ ${\displaystyle \underset{}{\le }}$ x ${\displaystyle \underset{}{\le }}$ ${\displaystyle \underset{}{1}}$ ${\displaystyle f\underset{}{}{}^{}}$(${\displaystyle n^{}}$+ ${\displaystyle 1^{}}$)${\displaystyle {}^{}}$( ${\displaystyle x}$) ${\displaystyle \le }$ ${\displaystyle {}_{}}$ ${\displaystyle n_{}}$+ ${\displaystyle 1_{}}$ ${\$

그러므로,

${\displaystyle \underset{}{max}}$- ${\displaystyle \underset{}{1}}$ ${\displaystyle \underset{}{\le }}$ ${\displaystyle \underset{}{x}}$ ${\displaystyle \underset{}{\le }}$ 1 ${\displaystyle f\underset{}{}}$ ${\displaystyle (x}$)${\displaystyle }$- ${\displaystyle P_{}}$ n${\displaystyle {}_{}}$(${\displaystyle x}$) ${\displaystyle \le }$ ${\displaystyle {Mn}_{}}$+ 1 ${\displaystyle {\mathrm{h}}_{}}$ ${\displaystyle \frac{n^{}}{}}$+ ${\displaystyle \frac{1^{}}{}}$(${\displaystyle \frac{\mathrm{n}}{}}$+ 1${\displaystyle \frac{}{}}$) ${\$ _${-1\leq$ x$\leq$ 1} f$(x)-P_{n}(x) \leq M_{n+1}{\frac {h^{n+1}}{(n+1$

그러나 ${\displaystyle N_{}}$+ ${\displaystyle 1_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle (n}$+ ${\displaystyle 1)!}$ 5 ${\displaystyle {\mathrm{n}}^{}}$+ 1 ${\$이기 때문에 n이 증가하면 룽지 함수의 (n+1)번째 도함수의 크기가 증가합니다.$^{n+1$ 결과적으로, 결과적으로 상한인 $({\displaystyle 10}$/ n${\displaystyle {}^{}}$) ${\displaystyle n^{}}$+ ${\displaystyle 1^{}}$ ${\displaystyle {}^{}}$! ${\displaystyle (10$/ $n)^{n+1}n$은 n이 무한대인 경향이 있을 때 무한대인 경향이 있습니다.

룽지 현상을 설명하는 데 자주 사용되지만, 오차의 상한이 무한대로 간다는 사실이 물론 오차 자체도 n과 함께 발산한다는 것을 의미하지는 않습니다.

완화

보간점 변경

간격의 $가장자리$^[3], 특히 공식 1${\displaystyle }$/ 1${\displaystyle \sqrt{}}$- ${\displaystyle x\sqrt{\mathrm{}}}$ ${\displaystyle \sqrt{{2\mathrm{}}^{}}}$ ${\$ 1$/{\sqrt {1-x^{2}}}$에 의해 주어진 점근 밀도(구간 [-1, 1])를 사용하여 진동을 최소화할 수 있습니다$.$ 이러한 노드 집합의 표준 예는 Chebyshev 노드입니다. 이 경우 룽지 함수를 근사하는 데 있어 최대 오차는 다항식 차수가 증가함에 따라 감소하는 것이 보장됩니다.

재샘플링 없는 S-Runge 알고리즘

잘 작동하는 노드 집합에서 재샘플링이 불가능하기 때문에 등거리 샘플을 사용해야 하는 경우 S-Runge 알고리즘을 고려할 수 있습니다.^[4] 이 접근법에서 원래 노드 집합은 Chebyshev 노드 집합에 매핑되어 안정적인 다항식 재구성을 제공합니다. 이 방법의 특이점은 매핑된 노드에서 리샘플링을 할 필요가 없다는 것인데, 이를 페이크 노드라고도 합니다. 이 절차의 Python 구현은 여기에서 확인할 수 있습니다.

구간 다항식의 사용

분할 다항식인 스플라인 곡선을 사용하면 문제를 피할 수 있습니다. 보간 오차를 줄이려고 할 때 사용되는 다항식의 정도를 증가시키는 대신 스플라인을 구성하는 데 사용되는 다항식의 수를 증가시킬 수 있습니다.

제한적 최소화

더 높은 차수의 다항식을 맞출 수도 있습니다(예를 들어, n ${\displaystyle$ n$}$개의 점에서 n + 1 {\displaystyle n+1} 대신 $n$ = ${\displaystyle {}^{}}$ ${\$$displaystyle$ N = n^{$2$}} 차수의 다항식을 사용하고, 첫 번째(또는 두 번째) 도함수가 최소 L 2 {\displaystyle L^{2} 노름을 갖는 보간 다항식을 맞출 수도 있습니다.

유사한 접근법은 다항식의 $m{\displaystyle }$ ${\displaystyle$ m$}$번째$$ 도함수와 $m{\displaystyle }$ ${\displaystyle$ m$}$번째$$ 도함수의 평균값 사이의 ${\displaystyle {제한}^{}}$된 버전의$Lp$ {\$displaystyle$ L$^{p}$ 거리를$$ 최소화하는 것입니다. 명시적으로, 최소화하기 위해

${\displaystyle V_{p}=\int _{a}^{b}\left {\frac {\mathrm {d} ^{m}P_{N}(x)}{\mathrm {d} x^{m}}}-{\frac {1}{b-a}}\int _{a}^{b}{\frac {\mathrm {d} ^{m}P_{N}(z)}{\mathrm {d} z^{m}}}\mathrm {d} z\right ^{p}\mathrm {d} x-\sum _{i=1}^{n}\lambda _{i}\,\left(P_{N}(x_{i})-f(x_{i})\right),}$

${\displaystyle \mathrm{여기}}$서 다항식 계수 및 라그랑주$$에 대한 $N$≥ n - 1 ${\$$displaystyle N\$geq n - 및$m$ < N {\$displaystyle$ m N}, λ i$displaystyle$ \lambda _{i}. ${\displaystyle N}$ = n - 1 {\$displaystyle$ N= n-1}일${\displaystyle \mathrm{때}}$, 라그랑주 승수에 의해 생성된 제약 방정식은 P ${\displaystyle N_{}}$(${\displaystyle x)}$ ${\displaystyle P_{N}(x)}$을 모든 $n{\displaystyle }$ ${\displaystyle n}$개의$$ 점을 통과하는 최소 다항식으로 줄입니다$$. 반대쪽 끝에서, ${\displaystyle \underset{}{림}}$ ${\displaystyle N}$ → ∞ P N($x$) ${\displaystyle \lim_{N$\to $\infty}P_${N}(x)}는 조각 다항식 근사와 매우 유사한 형태로 접근할 것입니다. $m$ = ${\$displaystyle m=1}일 때, $특히$ lim N → ∞ P N(x) {\displaystyle \lim_{N\to \infty }P_{N}(x)}는 선형 조각 다항식, 즉 보간점을 직선으로 연결하는 것에 접근합니다.

$V{\displaystyle {}_{}}$ ${\displaystyle p_{}}$ ${\$를 최소화하는 과정에서$$ p ${\displaystyle p}$가 수행하는 역할은 평균값에서 벗어난 변동 크기의 중요도를 제어하는 것입니다$$. $p{\displaystyle }$ ${\displaystyle p}$가 클수록 작은 변동에 비해 큰 변동이 불이익을 받습니다. 유클리드 $노름$인 p = ${\displaystyle 2}$ ${\$displaystyle $p$$$= 2}의 가장 큰 장점은 분석 솔루션을 허용하고 V p {\displaystyle V_{p}가 최소값을 단 하나만 가질 것을 보장한다는 것입니다. $p$≠ 2일 때 ${\displaystyle$ p\n$eq 2}$ V ${\displaystyle p_{}}$ ${\$에는 여러 개의 최소값이 있을$$ 수 있으므로$$발견된 특정 최소값이 로컬 최소값이 아닌 전역 최소값이 되도록 보장하기가 어렵습니다.

최소 자승 적합

또 다른 방법은 최소 제곱법을 사용하여 더 낮은 차수의 다항식을 맞추는 것입니다. 일반적으로 $m{\displaystyle }$ ${\displaystyle$ m$}$ 등거리$$ 점을 사용할 때 N< 2 ${\$ N$<2{\sqrt {m}}$이면 최소 제곱 근사치 ${\displaystyle P_{}}$ N${\displaystyle {}_{}x)}${\$displaystyle P_{N}(x)}$가 잘 조절됩니다.^[5]

번스타인 다항식

번스타인 다항식을 사용하면 모든 연속 함수를 닫힌 구간에서 균일하게 근사할 수 있지만 이 방법은 계산 비용이 다소 많이 듭니다.^{[citation needed]}

외부 가짜 제약 조건 보간

이 방법은 유형 P ″(x) = 0의 제약의 조밀한 분포를 보간 간격의 각 변의 끝점 근처에 외부에 위치한 노드에 최적으로 적층하는 것을 제안합니다. 여기서 P(x)는 보간 다항식의 2차 도함수입니다. 이러한 제약 조건은 보간 간격에 속하지 않고 룬지 함수의 동작과 일치하지 않으므로 외부 가짜 제약 조건이라고 합니다. 이 방법은 룽지 현상을 완화하기 위해 조각 다항식(스플라인)보다 더 나은 보간 성능을 가지고 있음을 입증했습니다.^[6]

근사 이론에서 나온 관련 진술

미리 정의된 모든 보간 노드 테이블에 대해 해당 노드에 대한 보간 다항식의 시퀀스가 분기되는 연속 함수가 있습니다.^[7] 모든 연속 함수에 대해 보간 과정이 수렴하는 노드 테이블이 있습니다.^{[citation needed]} 체비셰프 보간(즉, 체비셰프 노드에서)은 모든 절대 연속 함수에 대해 균일하게 수렴합니다.

참고 항목

• 체비셰프 노드
• 사인곡선 기저함수에 대한 깁스 현상과 비교
• Occam의 면도기는 더 단순한 모델을 주장합니다.
• 수렴 실패의 또 다른 예인 슈바르츠 랜턴
• 스톤-바이어스트라스 정리
• 테일러 급수
• 윌킨슨 다항식

참고문헌