반정형 다면체
Semiregular polyhedron |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
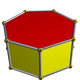 |  |  |  |
반정형 다면체(또는 반정형 다면체)라는 용어는 다른 저자들에 의해 다양하게 사용된다.
원래의 정의에서, 그것은 규칙적인 다각형의 얼굴을 가진 다면체이며, 정점에 전이적인 대칭군이다. 오늘날, 이것은 더 흔히 균일한 다면체라고 불린다(이것은 보다 일반적인 반정형 다면체의 1900년 정의에서 따온 것이다).[1][2] 이러한 다면체에는 다음이 포함된다.
- 13개의 아르키메데스 고형물.
- 볼록 프리즘의 무한 시리즈.
- 볼록한 일련의 대척점들 (그들의 반정맥적 성질은 케플러에 의해 처음 관찰되었다.)
이러한 반정형 고형물은 정점 구성에 의해 완전히 지정될 수 있다: 정점 주위에서 발생하는 순서대로 면의 숫자에 의한 얼굴 목록이다. 예를 들어: 3.5.3.5는 각 꼭지점을 중심으로 두 개의 삼각형과 두 개의 오각형을 번갈아 나타내는 이코시다데카헤드론을 나타낸다. 대조적으로 3.3.3.5는 오각형 항정신병이다. 이 다면체들은 때때로 정점-변환으로 묘사된다.
고셋 이후, 다른 작가들은 더 높은 차원의 폴리토페스와 관련하여 다른 방식으로 반정형이라는 용어를 사용해 왔다. E. L. Elte는[3] Coxeter가 너무 인위적이라고 발견한 정의를 제공했다. 콕시터 자신은 고셋의 수치를 균일하다고 불렀는데, 반정형으로 분류되는 부분집합만 상당히 제한되어 있었다.[4]
그러나 다른 사람들은 더 많은 다면체를 반정형으로 분류하면서 반대 방향으로 나아갔다. 여기에는 다음이 포함된다.
- 고셋의 정의에 부합하는 항성 다면체 3세트는 위에서 열거한 세 가지 볼록 세트와 유사하다.
- 위의 반정형 고형물의 이중들은 이중 다면체가 원형과 동일한 대칭을 공유하기 때문에 그것들 역시 반정형으로 보아야 한다고 주장한다. 이 이중에는 카탈로니아 고형물, 볼록한 디피라미드, 볼록한 반디피라미드 또는 사다리꼴라와 그 비콘벡스 유사점이 포함된다.
혼란의 또 다른 원인은 아르키메데스 고형물이 정의되는 방식에 있으며, 다시 다른 해석이 나타난다.
고셋의 반정형 정의는 더 높은 대칭의 그림인 정형과 정각형 다면체를 포함한다. 일부 후기 저자들은 이것들이 반정형이 아니라고 말하는 것을 선호한다. 왜냐하면 그들은 그것보다 더 규칙적이기 때문이다 - 균일한 다면체는 정규, 준정형, 그리고 반정형 다면체를 포함하고 있다고 한다. 이 명명 체계는 잘 작동하며, 혼돈의 많은 (그러나 결코 전부는 아니다)를 조정한다.
실제로 가장 저명한 권위자들조차 혼란을 겪을 수 있으며, 주어진 다면체 세트를 반정형 및/또는 대정형으로 정의하고, 이후 논의에서 다른 세트를 가정(또는 언급)할 수도 있다. 어떤 사람이 명시한 정의를 볼록한 다면체에만 적용한다고 가정하는 것은 아마도 가장 흔한 실패일 것이다. Coxeter, Cromwell,[5] Cundy & Rollett는[6] 모두 그러한 실수를 범했다.
일반적 발언
많은 작품에서 반정형 다면체는 아르키메데스 고체의 동의어로 사용된다.[7] 예를 들어, Cundy & Rollett (1961년).
우리는 고셋을 바탕으로 한 안면정규형과 정점변환형, 그리고 그들의 수직정규형(또는 베르시정규형)과 안면변환형 이중형을 구분할 수 있다.
Coxeter 외 연구진(1954)은 반정형 다면체라는 용어를 사용하여 아르키메데스 고형물 중 6개만을 포함하는 정의인 pq r 형식의 와이토프 기호가 있는 균일한 다면체(Polyhedra)와 정규 프리즘(그러나 일반 항정신병) 및 수많은 비콘벡스 고형분을 분류한다. 후에 콕시터(1973)는 고셋의 정의를 코멘트 없이 인용하여 함축적으로 받아들이게 된다.
에릭 와이스슈타인, 로버트 윌리엄스 등은 아르키메데스 고형물, 균일한 프리즘, 균일한 항정신병(입방체를 프리즘으로, 정규 옥타헤드론을 항정신병으로서 겹침)을 포함한 5개의 규칙적인 다면체를 제외한 볼록한 균일한 다면체를 의미하기 위해 이 용어를 사용한다.[8][9]
피터 크롬웰(1997)은 149페이지의 각주에 "현재의 용어로는 '세미레겔 다면체'는 아르키메데스와 카탈루냐 (아키메데스 이중) 고체를 가리킨다"고 적고 있다. 80페이지에서 그는 13명의 아르키메데인을 반관형으로 묘사하는 반면 367페이지에 묘사했다. 그는 카탈로니아인들과 그들의 '세습적인' 아르키메데인과의 관계에 대해 논한다. 함축적으로 이것은 카탈로니아인들을 반정형적이 아닌 것으로 취급하며, 따라서 그가 앞 각주에 제공한 정의와 효과적으로 모순된다(또는 적어도 혼란스럽게 한다). 그는 비콘벡스 다면체를 무시한다.
참고 항목
참조
- ^ 수학의 메신저, 맥밀런, 1900년 N차원의 정규 및 반정규격 인물에 관한 소럴드 고셋
- ^ Coxeter, H.S.M. 정규 폴리토페스, 3번째 Edn, Dover (1973)
- ^ Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen
- ^ H.S.M., M.S., Miller, J.C.P., Longuet-Higgins, M.S., Miller. 제복 폴리헤드라, 런던 왕립 협회의 철학 거래 (1954년), 페이지 401-450 (JSTOR 아카이브, 가입 필요)
- ^ Cromwell, P. P. P. Polyedra, Cambridge University Press (1977년)
- ^ Cundy H.M과 Rollett, A.P. Mathemical models, 제2 Edn. 옥스퍼드 대학교 출판부 (1961년)
- ^ 아르키메데스. (2006). 브리태니커 백과사전. 2006년 12월 19일 브리태니커 백과사전 온라인에서 검색됨(가입 필요).
- ^ Weisstein, Eric W. "Semiregular polyhedron". MathWorld. 여기서의 정의는 모든 얼굴이 합치되는 경우를 배제하지 않지만, 플라토닉 고형물은 기사의 열거에 포함되지 않는다.
- ^ Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (3장: 폴리헤드라)