포함-배제원칙

포함-배제 원리(inclusion-exclusion principle)는 두 개의 유한 집합의 결합에서 원소의 수를 구하는 친숙한 방법을 일반화하는 계산 기법입니다.

${\displaystyle A\cup B = A + B - A\cap B}$

여기서 A와 B는 두 개의 유한 집합이고 S는 집합 S의 카디널리티(집합이 유한한 경우 집합의 원소 개수로 간주될 수 있음)를 나타냅니다. 공식은 일부 요소를 두 번 셀 수 있으므로 두 집합의 크기의 합이 너무 클 수 있다는 사실을 표현합니다. 이중 카운트된 요소는 두 집합의 교차점에 있는 요소이며 교차점의 크기를 빼서 카운트를 수정합니다.

포함-배제 원리는 두 집합의 경우를 일반화한 것으로서, 집합 A, B, C에 대하여 다음과 같이 주어진 세 집합의 경우에 더 명확하게 보일 수 있습니다.

${\displaystyle A\cup B\cup C = A + B + C - A\cap B - A\cap C - B\cap C + A\cap B\cap C}$

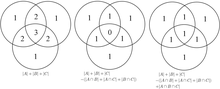
이 공식은 벤 다이어그램 그림의 각 영역이 공식의 오른쪽에 몇 번이나 포함되어 있는지 세어 확인할 수 있습니다. 이 경우, 과도하게 계산된 요소의 기여도를 제거할 때, 세 집합의 상호 교점에 있는 요소의 수가 너무 자주 차감되었기 때문에 정확한 합계를 얻으려면 다시 추가해야 합니다.

이러한 예제의 결과를 일반화하면 포함-배제의 원리를 얻을 수 있습니다. n개 집합의 합집합의 카디널리티를 구하는 방법:

1. 집합의 기수를 포함합니다.
2. 쌍대 교차점의 기수를 제외합니다.
3. 삼중 교차점의 기수를 포함합니다.
4. 4각 교차점의 기수를 제외합니다.
5. 5등분 교차점의 기수를 포함합니다.
6. n개의 쌍방향 교차점의 카디널리티가 포함되거나(n이 홀수인 경우) 제외될 때까지 계속합니다(n이 짝수인 경우).

그 이름은 그 원칙이 과도한 포함에 기초하고, 그 다음에 배제를 보상한다는 생각에서 비롯되었습니다. 이 개념은 비록 Daniel da Silva (1854)^[2]의 논문에 처음 등장하고 이후 J. J. Silva (1883)의 논문에 등장하지만,^[1] Abraham de Moivre (1718)에 기인합니다.^[3] 때때로 이러한 출판물 때문에 이 원리는 다 실바 또는 실베스터의 공식으로 언급됩니다. 이 원리는 수론에서 광범위하게 사용되는 체법의 한 예로 볼 수 있으며 체 공식으로 불리기도 합니다.^[4]

유한 확률은 확률 공간의 카디널리티에 대한 카운트로 계산되므로 포함-배제 원리에 대한 공식은 집합의 카디널리티가 유한 확률로 대체되는 경우에도 유효합니다. 좀 더 일반적으로, 두 가지 버전의 원리는 측정 이론이라는 공통 우산 아래 놓일 수 있습니다.

매우 추상적인 설정에서 포함-배제의 원리는 특정 행렬의 역산으로 표현될 수 있습니다.^[5] 이 역원은 특별한 구조를 가지고 있어서 이 원리는 조합학과 수학의 관련 분야에서 매우 귀중한 기술이 됩니다. 지안 카를로 로타의 말대로:^[6]

이산 확률과 조합 이론에서 가장 유용한 열거 원리 중 하나는 포함-배제의 유명한 원리입니다. 능숙하게 적용했을 때, 이 원리는 많은 조합적인 문제에 대한 해결책을 산출해냈습니다."

공식

일반적인 공식에서 포함-배제의 원리는 유한 집합 A에₁ 대하여, ..., A는_n 다음과 같은 항등식을 갖는다는 것을 말합니다.

${\displaystyle \left \bigcup _{i=1}^{n}A_{i}\right =\sum _{i=1}^{n} A_{i} -\sum _{1\leqslant i<j\leqslant n} A_{i}\cap A_{j} +\sum _{1\leqslant i<j<k\leqslant n} A_{i}\cap A_{j}\cap A_{k} -\cdots +(-1)^{n+1}\left A_{1}\cap \cdots \cap A_{n}\right .}$

(1)

이것은 압축적으로 다음과 같이 쓸 수 있습니다.

${\displaystyle \left \bigcup _{i=1}^{n}A_{i}\right =\sum _{k=1}^{n}(-1)^{k+1}\left(\sum _{1\leqslant i_{1}<\cdots <i_{k}\leqslant n} A_{i_{1}}\cap \cdots \cap A_{i_{k}} \right)}$

아니면

${\displaystyle \left \bigcup _{i=1}^{n}A_{i}\right =\sum _{\emptyset \neq J\subseteq \{1,\ldots ,n\}}(-1)^{ J +1}\left \bigcap _{j\in J}A_{j}\right .}$

즉, 유한 집합들의 유한 결합에 있는 원소들의 수를 세기 위해서는 먼저 개별 집합들의 기수를 합한 다음, 적어도 두 집합에 나타나는 원소들의 수를 뺀 다음, 적어도 세 집합에 나타나는 원소들의 수를 다시 더한 다음, 적어도 네 집합에 나타나는 원소들의 수를 뺀 다음, 등등. 이 프로세스는 항상 종료됩니다. (예를 들어, $n$ = ${\displaystyle 4}$이면$$$$displaystyle n = 4,} 집합이 4개를 초과하면 {\$displaystyle$ n = 4,} 집합에 나타나는 요소가 없을 수 있습니다. 마찬가지로 5개 이상의 {\displaystyle 5} 집합에 나타나는 요소도 있을 수 없습니다.)

응용 분야에서 원칙은 보완적인 형태로 표현되는 것이 일반적입니다. 즉, S를 모든 A를 포함하는 유한한 보편 집합이라 $하고$, $Ai를$¯ ${\displaystyle {\a_${i$}}}$라고 하면, 드 모르간의 법칙에 의해 S에서 A의 여집합을 나타냅니다.

${\displaystyle \left \bigcap_{i=1}^{n}{\bar {A_{i}}}\right =\left S-\bigcup_{i=1}^{n}A_{i}\right = S -\sum _{i=1}^{n} A_{i} +\sum _{1\leqslant i<j\leqslant n} A_{i}\cap A_{j} -\cdots +(-1)^{n} A_{1}\cap \cdots \cap A_{n} .}$

문장의 또 다른 변형으로 P₁, ..., P를_n 집합 S의 원소들이 가질 수도 있고 가지지 않을 수도 있는 성질들의 목록이라고 하자. 포함-배제의 원리는 어떤 성질도 가지지 않는 S의 원소들의 수를 계산하는 방법을 제공합니다. A를_i 성질 P를_i 갖는 S의 원소들의 부분집합으로 하고 그 원리를 상보적인 형태로 사용하자. 이 변종은 J. J. 실베스터 때문입니다.^[1]

오른쪽에 있는 첫 번째 m<n의 합(원칙의 일반적인 형태)만 고려하면 m이 홀수이면 과대평가를 받고 m이 짝수이면 과소평가를 받게 됩니다.

예

정수를 세는 중

포함-배제 원칙을 사용하는 간단한 예로 다음과 같은 질문을 생각해 보십시오.^[7]

{1, …, 100}의 몇 개의 정수가 2, 3, 5로 나누어지지 않습니까?

S = {1,…,100} 그리고 P는 정수가 2로 나뉠 때의 성질, P는 정수가 3으로 나뉠 때의 성질, P는 정수가 5로 나뉠 때의 성질을 말합니다. 원소들이 기본적으로 계수함으로써 성질 P를_i 갖는 S의 부분집합이 A라고_i 하자: A = 50, A = 33, A = 20입니다. 이 정수들 중 16개는 6으로, 10개는 10으로, 6개는 15로 나뉩니다. 마지막으로 30으로 나뉠 수 있는 정수는 3개뿐이므로 2, 3, 5 중 어느 것으로도 나뉠 수 없는 정수의 수는 다음과 같습니다.

100 − (50 + 33 + 20) + (16 + 10 + 6) − 3 = 26.

이탈 계수

좀 더 복잡한 예는 다음과 같습니다.

1부터 n까지 번호가 매겨진 n개의 카드 덱이 있다고 가정해 보자. m이라는 번호가 붙은 카드가 갑판의 m번째 카드일 경우 올바른 위치에 있다고 가정합니다. W, 최소 한 장의 카드가 올바른 위치에 있을 때 몇 가지 방법으로 카드를 섞을 수 있습니까?

먼저 m번째 카드가 올바른 카드의 모든 순서인 집합 A를_m 정의합니다. 그렇다면 주문 수 W는 하나 이상의 카드가 올바른 위치에 있는 경우 m은 다음과 같습니다.

${\displaystyle W=\left \bigcup _{m=1}^{n}A_{m}\right.}$

포함-배제의 원칙을 적용하고,

${\displaystyle W=\sum _{m_{1}=1}^{n} A_{m_{1}} -\sum _{1\leqslant m_{1}<m_{2}\leqslant n} A_{m_{1}}\cap A_{m_{2}} +\cdots +(-1)^{p-1}\sum _{1\leqslant m_{1}<\cdots <m_{p}\leqslant n} A_{m_{1}}\cap \cdots \cap A_{m_{p}} +\cdots }$

각 값 ${\displaystyle {Am}_{}}$ ${\displaystyle 1_{}}$∩ ⋯ ∩$Amp$ {\$displaystyle A_{$m_{1}}\cap \cap A_{m_{p}}는 p개 이상의 값 m, …, m을 올바른 위치에 갖는 셔플 집합을 나타냅니다. 적어도 p 값이 정확한 셔플의 수는 $m{\displaystyle }$ ${\displaystyle$ m$}$의 특정 값에 의존하지 않고 p에만 의존합니다$.$ 예를 들어, 1, 3, 17번째 카드가 정확한 위치에 있는 셔플의 수는 2, 5, 13번째 카드가 정확한 위치에 있는 셔플의 수와 같습니다. n개의 카드 중에서 3개가 올바른 위치에 있도록 선택되었다는 것만 중요합니다. 따라서 p번째 합에는$$($n\genfrac{}{}{0ex}{}{p}{}$) {\$textstyle {n \choose$ p$}}$개의$$ 동항이 있습니다(조합 참조).

${\displaystyle W={n \choose 1} A_{1} -{n \choose 2} A_{1}\cap A_{2} +\cdots +(-1)^{p-1}{n \choose p} A_{1}\cdots \cap A_{p} +\cdots }$

${\displaystyle {}_{}{}_{}{1}_{}}$∩ ⋯ ∩ $Ap$ {\$displaystyle$A_{1}\capdots \cap A_{p} }은 p개의 원소가 올바른 위치에 있는 순서의 수이며, 이는 나머지 n개의 원소를 순서화하는 방법의 수 또는 (n - p!)와 같습니다. 이렇게 해서 우리는 마침내 다음을 얻게 됩니다.

${\displaystyle {\begin{aligned}W&={n \choose 1}(n-1)!-{n \choose 2}(n-2)!+\cdots +(-1)^{p-1}{n \choose p}(n-p)!+\cdots \\&=\sum _{p=1}^{n}(-1)^{p-1}{n \choose p}(n-p)!\\&=\sum _{p=1}^{n}(-1)^{p-1}{\frac {n!}{p!(n-p)!}}(n-p)!\\&=\sum _{p=1}^{n}(-1)^{p-1}{\frac {n!}{p!}}\end{align}}}$

올바른 위치에 카드가 없는 치환을 디레인지먼트(derrange)라고 합니다. n!을 순열의 총 개수라고 할 때, 임의의 셔플이 어긋남을 생성할 확률 Q는 다음과 같이 주어집니다.

${\displaystyle Q=1-{\frac {W}{n!}}=\sum _{p=0}^{n}{\frac {(-1)^{p}}{p!}},}$

e의⁻¹ 테일러 전개의 n+1항에 대한 절단 따라서 여러 개의 카드가 뒤섞여 있는 주문을 추측하고 모든 카드에 대해 틀릴 확률은 약⁻¹ e 또는 37%입니다.

특별한 경우

위의 탈선 사례에서 나타나는 상황은 특별한 주의를 기울일 가치가 있을 정도로 자주 발생합니다.^[8] 즉, 포함-배제 원리 공식에 나타나는 교차점 집합의 크기가 교차점의 집합 수에만 의존하고 어떤 집합이 나타나는지에 의존하지 않습니다. 좀 더 형식적으로, 교차점이

${\displaystyle A_{J}:=\bigcap _{j\in J}A_{j}}$

{1, …, n}의 모든 k-element 부분 집합 J에 대하여 동일한 카디널리티(예: α = A)를 가지면,

${\displaystyle \left \bigcup _{i=1}^{n}A_{i}\right =\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}\alpha _{k}.}$

또는, 보편 집합 S가 카디널리티 α를₀ 갖는 상보형에서는,

${\displaystyle \left S\smallset minus \bigcup _{i=1}^{n}A_{i}\right =\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}\alpha _{k}.}$

수식 일반화

보편 집합 S의 부분집합₁₂ A, A, ..., A의_n 가군(반복 허용)이 주어지면, 포함-배제의 원리는 이들 부분집합 중 어느 것에도 포함되지 않는 S의 원소의 개수를 계산합니다. 이 개념을 일반화하면 이들 집합 중 정확히 일부 고정된 m에 나타나는 S의 원소의 수를 계산할 수 있습니다.

Let N = [n] = {1,2,…,n}. $A$ ∅ = S ${\$displaystyle A_{\emptyset} = S}를 정의하면 이전 섹션의 표기법을 사용하여 포함 – exclusion의 원리를 다음과 같이 나타낼 수 있습니다. A에 포함되지 않은 S의 요소 수는 다음과 같습니다.

${\displaystyle \sum_{J\subseteq [n]}(-1)^{J} A_{J}.}$

I가 인덱스 집합 N의 고정 부분 집합일 경우, I의 모든 i에 대해_i A에 속하고 다른 값이 없는 원소의 수는 다음과 같습니다.^[9]

${\displaystyle \sum_{I\subseteq J}(-1)^{ J - I } A_{J}.}$

집합 정의

${\displaystyle B_{k}=A_{I\cup \{k\}}{\text{ for }}k\in N\smallsetminus I.}$

포함 – exclusion의 원리(${\displaystyle B_{}{}_{}}$∅ = $AI {\displaystyle$ B_{\emptyset} = A_{I})에 따라 B에 포함되지 않는 원소의 수를 구합니다.

${\displaystyle \sum_{K\subseteq N\smallsetminus I}(-1)^{K } B_{K}.}$

N \ I의 부분집합과 I을 포함하는 N의 부분집합 사이의 대응 K ↔ J = I ∪ K는 사영이며, 이 지도 아래에서 J와 K가 대응하면 B = A가 됩니다.

비확률적으로

확률적으로${\displaystyle ,}$ 확률 공간$$(ω exclusion$,$ F, P) ${\displaystyle (\Omega$, ${\mathcal$ {$F}},\mathbb${P})}에서, 포함-– 원리는 n = 2가 됩니다.

${\displaystyle \mathbb {P} (A_{1}\cup A_{2})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})-\mathbb {P} (A_{1}\cap A_{2}),}$

n=3의 경우

${\displaystyle \mathbb {P} (A_{1}\cup A_{2}\cup A_{3})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})+\mathbb {P} (A_{3})-\mathbb {P} (A_{1}\cap A_{2})-\mathbb {P} (A_{1}\cap A_{3})-\mathbb {P} (A_{2}\cap A_{3})+\mathbb {P} (A_{1}\cap A_{2}\cap A_{3})}$

그리고 일반적으로

${\displaystyle \mathbb {P} \left(\bigcup _{i=1}^{n})A_{i}\right)=\sum _{i=1}^{n}\mathbb {P} (A_{i})-\sum _{i<j}\mathbb {P} (A_{i}\cap A_{j})+\sum _{i<j<k}\mathbb {P} (A_{i}\cap A_{j}\cap A_{k})+\cdots +(-1)^{n-1}\sum _{i<...<n}\mathbb {P} \left(\bigcap _{i=1}^{n}A_{i}\right),}$

다음과 같이 폐쇄형으로 작성할 수 있습니다.

${\displaystyle \mathbb {P} \left(\bigcup _{i=1}^{n})A_{i}\right)=\sum _{k=1}^{n}\left((-1)^{k-1}\sum _{I\subseteq \{1,\ldots ,n\} \atop I =k}\mathbb {P} (A_{I})\right),}$

마지막 합이 정확히 k개의 원소를 포함하는 인덱스 1, …, n의 모든 부분 집합 I에 걸쳐 있는 경우,

${\displaystyle A_{I}:=\bigcap _{i\in I}A_{i}}$

A와 I의 지수의_i 교집합을 나타냅니다.

Bonferroni 부등식에 따르면, 공식의 첫 번째 항들의 합은 교대로 LHS의 상한과 하한입니다. 전체 공식이 너무 번거로운 경우에 사용할 수 있습니다.

일반 측도 공간(S, σ,μ)과 유한 측도의 측정 가능한 부분 집합 A, …, A의 경우, 확률$측도$ P${\displaystyle \mathbb$ {P}}가 측도 μ로 대체될 때 위 항등식은 유지됩니다.

특수한 경우

포함-배제 원리의 확률론적 버전에서 교집합 A의_I 확률이 I의 카디널리티에만 의존한다면, 이는 {1, …, n}의 모든 k에 대하여_k 다음과 같은 a가 존재함을 의미합니다.

${\displaystyle a_{k}=\mathbb {P}(A_{)I}){\text{ for ever}}{\dots,n\}{\text{ with }} I = k,}$

그러면 위의 공식은 다음과 같이 단순화됩니다.

${\displaystyle \mathbb {P} \left(\bigcup _{i=1}^{n})A_{i}\right)=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}a_{k}}$

이항 계수$$($n$ $\genfrac{}{}{0ex}{}{k}{})$ ${\textstyle {\binom {n}{k}}$의 조합 해석으로 인해$.$ 예를 들어, 이벤트 ${\displaystyle {Ai}_{}}$ ${\displaystyle A_{i}}$가 독립적이고 동일하게 분포되어 있다면, 모든 i에 $대해$ P${\displaystyle }$(${\displaystyle {Ai}_{}}$ = ${\displaystyle p}$ ${\displaystyle$\mathbb {P} (A_{i}) = p}, ${\displaystyle {그리고}_{}}$ k = ${\displaystyle p}$k {\displaystyle a_{k} = p^{k}} 가 있으며, 이 경우 위 식을 다음과 같이 단순화합니다.

${\displaystyle \mathbb {P} \left(\bigcup _{i=1}^{n})A_{i}\right)=1-(1-p)^{n}.}$

(이 결과는 이벤트 ${\displaystyle {Ai}_{}}$ ${\$의 보형물의 교집합을 고려하여 보다 간단하게 도출할 수도 있습니다.)$$

일반 측도 공간(S, σ, μ)과 유한 측도의 측정 가능한 부분 집합 A, …, A의 경우에도 유사한 단순화가 가능합니다.

기타식

원칙은 때때로 다음과 같은 형태로^[10] 명시됩니다.

${\displaystyle g(A)=\sum _{S\subseteq A}f(S)}$

그리고나서

${\displaystyle f(A)=\sum _{S\subseteq A}(-1)^{ A - S }g(S)}$

(⁎⁎)

포함-배제 원리의 조합형 및 확률형 버전은 (⁎⁎)의 예입니다.

$만약$ 어떤$$숫자 n {\$displaystyle$ n$}$을 그것의 소인수 집합으로 본다면, (⁎⁎)는 정사각형이 없는 자연수에 대한 뫼비우스 반전 공식의 일반화입니다. 따라서 (⁎⁎)는 A의 모든 부분 집합의 부분 순서 집합의 발생 대수에 대한 뫼비우스 반전 공식으로 간주됩니다.

뫼비우스 반전 공식의 전체 버전의 일반화를 위해서는 (⁎⁎을) 다중 집합으로 일반화해야 합니다. 집합이 아닌 다중 집합의 경우, (⁎⁎)는

${\displaystyle f(A)=\sum _{S\subseteq A}\mu (A-S)g(S)}$

(⁎⁎⁎)

여기서 $A{\displaystyle }$- ${\displaystyle S}$ ${\displaystyle A-S}$는$$(${\displaystyle A}$- S${\displaystyle )}$ ⊎ $S$ = A ${\displaystyle$ ($A-S)\$uplus S = A}에 대한 다중 집합이고,

• S가 짝수 카디널리티의 집합(즉, 이중 요소가 없는 다중 집합)일 경우 μ(S) = 1.
• S가 홀수 카디널리티의 집합(즉, 이중 원소가 없는 다중 집합)일 경우 μ(S) = -1.
• S가 적절한 다중 집합이면 μ(S) = 0입니다(즉, S는 이중 요소를 갖습니다).

$\mu {\displaystyle }$(${\displaystyle A}$- ${\displaystyle S}$) ${\displaystyle \mu ($A - S$)}$는$$A - S {\$display$ A - S$}$가 집합인${\displaystyle }경우$ (⁎⁎)의 ${\displaystyle (-1{}^{}}$ ${\displaystyle A^{}}$- ${\displaystyle S^{}}$ $display (-1)^{ A$- $S}$일 뿐입니다.

적용들

포함-배제 원칙은 널리 사용되고 있으며, 여기서 몇 가지 적용 사례만 언급할 수 있습니다.

이탈 계수

포함-배제 원리의 잘 알려진 응용은 유한 집합의 모든 차수를 계산하는 조합 문제입니다. 집합 A의 어긋남은 A에서 고정점이 없는 자기 자신으로의 사영입니다. 포함-배제 원리를 통해 A의 카디널리티가 n이면, 디어런스의 수는 [n! / e]이고, 여기서 [x]는 x에 가장 가까운 정수를 나타냅니다. 자세한 증명은 여기서 확인할 수 있으며 위의 예제 섹션도 참조하십시오.

이상 횟수를 세는 문제의 첫 번째 발생은 P. R. de Montmort (1678–1719)의 Essaid 'analy surles jeux de hazard'라는 우연한 게임에 관한 초기 책에 있으며, "Montmort의 문제" 또는 "problem de rencontres"라는 이름으로 알려져 있습니다.^[11] 이 문제는 모자 검사 문제라고도 합니다.

교호작용의 수는 n의 하위 인자라고도 하며, !n으로 적습니다. 따라서 모든 바이젝션에 동일한 확률이 할당되면 n이 증가함에 따라 랜덤 바이젝션이 분산일 확률이 1/e에 빠르게 접근합니다.

교차로수 계산

포함-배제의 원리는 De Morgan의 법칙과 결합하여 집합들의 교집합의 카디널리티를 계산하는 데에도 사용될 수 있습니다. $Ak$¯ {\displaystyle {\$overline {A_{$k}}}: 각 k에 대해$Ak$ ⊆ ${\displaystyle A_${k}\subseteq A${\displaystyle {}_{}}$가 되도록 일부 보편 집합 A에 대한 A의 여집합을 나타냅니다. 그러면 저희가.

${\displaystyle \bigcap_{i=1}^{n}A_{i}={\overline {\bigcup _{i=1}^{n}{\overline {A_{i}}}}}}$

교차점을 찾는 문제를 조합을 찾는 문제로 바꾸는 것입니다.

그래프 채색

포함 배제 원리는 그래프 색상과 같은 여러 NP-하드 그래프 분할 문제에 대한 알고리즘의 기초를 형성합니다.^[12]

이 원리의 잘 알려진 응용은 그래프의 색다항식을 구성하는 것입니다.^[13]

이분 그래프 완전 일치

이분 그래프의 완전 일치 수는 이 원리를 사용하여 계산할 수 있습니다.^[14]

온함수의 수

유한 집합 A와 B가 주어졌을 때, A에서 B까지의 사변함수는 몇 개인가요? 일반성을 잃지 않고 집합의 기수만 중요하므로 A = {1, ..., k} 및 B = {1, ..., n}을 취할 수 있습니다. S를 A에서 B까지의 모든 함수들의 집합으로 사용하고, B의 각 i에 대하여, 성질_i P를 "B의 원소 i가 일치하지 않는 함수"로 정의함으로써, 포함-배제의 원리는 A와 B 사이의 함수들의 수를 다음과 같이 제공합니다.^[15]

${\displaystyle \sum _{j=0}^{n}{\binom {n}{j}}(-1)^{j}(n-j)^{k}.}$

금지된 위치가 있는 순열

S의 각 원소가 특정 위치에 있지 않도록 제한되는 집합 S = {1, ..., n}의 순열을 금지된 위치를 가진 순열이라고 합니다. 예를 들어, S = {1,2,3,4}일 때, 원소 1은 1번 또는 3번 위치에 있을 수 없고, 원소 2는 4번 위치에 있을 수 없다는 제한을 갖는 순열은 2134, 2143, 3124, 4123, 2341, 2431, 3241, 3421, 4231 및 4321입니다. 원소 i가 들어갈 수 없는 위치의 집합을 A로_i 하고, 성질 P를_i 치환이 원소_i i를 A의 위치에 넣는 성질로 함으로써, 포함-배제의 원리를 사용하여 모든 제한을 만족하는 치환의 수를 셀 수 있습니다.^[16]

주어진 예제에서 성질이 P인 순열은 12 = 2(3!), 6 = 3! 성질이 P인 순열은 성질이 P 또는 P를 가지므로 이 두 요소에는 제한이 없습니다. 제한을 만족하는 순열의 수는 다음과 같습니다.

4! − (12 + 6 + 0 + 0) + (4) = 24 − 18 + 4 = 10.

이 계산에서 마지막 4는 속성₁ P와₂ P를 모두 갖는 순열의 수이다. 공식에 0이 아닌 다른 기여는 없습니다.

두 번째 종류의 스털링 수

두 번째 종류인 스털링 수 S(n,k)는 n개 원소 집합의 분할 수를 k개의 비어 있지 않은 부분 집합(구분할 수 없는 상자)으로 계산합니다. 이들에 대한 명시적인 공식은 매우 밀접하게 관련된 문제에 포함-배제의 원리를 적용함으로써 얻을 수 있습니다. 즉, n-집합의 파티션 수를 k개의 비어 있지 않지만 구별 가능한 상자(순서된 비어 있지 않은 부분집합)로 계산하는 것입니다. n-집합의 모든 분할들로 구성된 보편 집합을 k(아마도 비어있는) 구별 가능한 상자들₁, A, A₂, …, A로_k 사용하고, 분할이 상자 A를_i 비운다는 것을 의미하는 속성_i P를 사용하여, 포함-배제의 원리는 관련 결과에 대한 답을 제공합니다. 인위적인 순서를 제거하기 위해 k!로 나누면 두 번째 종류의 스털링 수가 나옵니다.^[17]

${\displaystyle S(n,k)={\frac {1}{k!}}\sum _{t=0}^{k}(-1)^{t}{\binom {k}{t}}(k-t)^{n}.}$

룩 다항식

루크 다항식은 바둑판의 정사각형의 부분집합처럼 보이는 보드 B에 공격하지 않는 루크를 배치하는 방법의 수를 생성하는 함수입니다. 즉, 두 개의 루크가 같은 행 또는 열에 있을 수 없습니다. 보드 B는 n개의 행과 m개의 열을 가진 직사각형 보드의 정사각형의 부분집합입니다. 우리는 이것을 루크를 넣을 수 있는 정사각형이라고 생각합니다. 루크 다항식 R_B(x)에서 x의^k 계수 r_k(B)는 루크가 다른 루크를 공격하지 않는 방법의 수로 B의 제곱에 배치될 수 있습니다. 임의의 보드 B의 경우, B에 없는 직사각형 보드의 정사각형으로 구성된$$ 보완 보드 $B{\displaystyle {}^{\text{'}}}$ ${\$ B$'}$가 있습니다. 이 보완 보드에는 계수 ${\displaystyle {rk}_{}{}^{}\text{'})}$인 루 다항식 ${\displaystyle {RB\text{'}(}_{}x)}$ ${\displaystyle R_{B'}(x)}$가 있습니다${\displaystyle .}$ ${\displaystyle r_{k}(B')}$

보완 보드의 루크 다항식의 계수로 볼 때 루크 다항식의 가장 높은 계수를 계산할 수 있는 것이 편리할 때가 있습니다. 일반성을 잃지 않고 n ≤ m이라고 가정할 수 있으므로 이 계수는_n r(B)입니다. 전체 n × m "체커보드"에 n개의 공격하지 않는 루크를 배치하는 방법의 수(루크를 보드 B의 사각형에 배치하는지 여부에 관계없이)는 다음과 같이 하락 요인에 의해 결정됩니다.

${\displaystyle (m)_{n}=m(m-1)(m-2)\cdots (m-n+1).}$

P를_i 전체 보드에 n개의 공격하지 않는 신인의 할당이 보드 B의 정사각형에 없는 신인 열 i를 갖는 속성으로 지정하면 포함-배제의 원칙에 따라 다음과 같습니다.^[18]

${\displaystyle r_{n}(B)=\sum _{t=0}^{n}(-1)^{t}(m-t)_{n-t}r_{t}(B').}$

오일러 파이 함수

오일러의 토텐티브 또는 파이 함수인 φ(n)은 상대적으로 소수에서 n보다 작거나 같은 양의 정수의 수를 세는 산술 함수입니다. 즉, n이 양의 정수이면, φ(n)은 1 이외의 n과 공통 인자가 없는 1 ≤ k ≤ n 범위의 정수 k의 개수입니다. 포함 배제의 원리는 φ(n)에 대한 공식을 얻기 위해 사용됩니다. S를 집합 {1, …, n}이라 하고, 성질 P를_i 1 ≤ i≤ r에 대하여 소수 p로_i 나누는 것으로 정의합니다. 여기서 소인수분해는 다음과 같습니다.

${\displaystyle n=p_{1}^{a_{1}}p_{2}^{a_{2}}\cdots p_{r}^{a_{r}}.}$

그러면.^[19]

${\displaystyle \varphi (n)=n-\sum _{i=1}^{r}{\frac {n}{p_{i}}}+\sum _{1\leqslant i<j\leqslant r}{\frac {n}{p_{i}p_{j}}}-\cdots =n\prod _{i=1}^{r}\left(1-{\frac {1}{p_{i}}}\right).}$

희석포용-배제원칙

원리가 정확한 공식(특히 에라토스테네스의 체를 사용하여 소수를 세는 것)을 제공할 수 있는 많은 경우, 발생하는 공식은 그 안의 항 수가 과도하기 때문에 유용한 내용을 제공하지 않습니다. 각 항을 개별적으로 정확하게 추정할 수 있는 경우 오류 누적은 포함-배제 공식이 직접 적용되지 않음을 의미할 수 있습니다. 수론에서 비고 브런은 이 문제를 해결했습니다. 천천히 시작한 후, 그의 아이디어는 다른 사람들에 의해 받아들여졌고, 매우 다양한 체법이 개발되었습니다. 예를 들어, 이들은 정확한 공식이 아니라 "체화된" 집합의 상한을 찾으려고 할 수 있습니다.

닫힌 단위 구간 [0_n, 1]에서 A₁, ..., A를 임의의 집합, p, ..., 실수라고_1n 합니다. 그러면 {0, …, n}의 모든 짝수 k에 대하여 지시 함수는 다음과 같은 부등식을 만족합니다.^[20]

${\displaystyle 1_{A_{1}\cup \cdots \cup A_{n}}\geq \sum _{j=1}^{k}(-1)^{j-1}\sum _{1\leq i_{1}<\cdots <i_{j}\leq n}p_{i_{1}}\dots p_{i_{j}}\,1_{A_{i_{1}}\cap \cdots \cap A_{i_{j}}}.}$

주진술증명

모든 집합의 합집합에 포함된 $원소$를 선택하고, ${\displaystyle {A1\mathrm{}}_{}}$ ${\displaystyle {A2\mathrm{}}_{}\dots ,}$ ${\displaystyle {At}_{}}${\$displaystyle A_{1}, A_{2},\dots, A_{t}$를 포함된 개별 집합이라고 합니다. (t > 0.) 원소는 식 (1)의 좌변에 의해 정확하게 한 번씩 계산되므로, 오른쪽으로 정확하게 한 번씩 계산된다는 것을 보여줘야 합니다. 오른쪽에서 0이 아닌 기여는 특정 항의 모든 부분 집합이 선택된 요소를 포함할 때만 발생합니다. 즉, 모든 부분 $집합$이 ${\displaystyle {A1\mathrm{}}_{}}$ ${\displaystyle {A2\mathrm{}}_{},}$ …에서$${\$displaystyle A_{1}, A_{2},\dots, A_{t}}$에서 선택됩니다$.$ 기여는 각 집합에 대해 하나이므로(기간에 따라 + 또는 -) 기간에 사용된 부분 집합의 (서명된) 개수에 불과합니다. 다음은 다음과 같습니다.

${\displaystyle {\begin{aligned} \{A_{i}\mid 1\leqslant i\leqslant t\} &- \{A_{i}\cap A_{j}\mid 1\leqslant i<j\leqslant t\} +\cdots +(-1)^{t+1} \{A_{1}\cap A_{2}\cap \cdots \cap A_{t}\} ={\binom {t}{1}}-{\binom {t}{2}}+\cdots +(-1)^{t+1}{\binom {t}{t}}.\end{align}}}$

이항 정리에 의해,

${\displaystyle 0=(1-1)^{t}={\binom {t}{0}}-{\binom {t}{1}}+{\binom {t}{2}}-\cdots +(-1)^{t}{\binom {t}{t}}.}$

$({\displaystyle t}$ 0${\displaystyle )}$ = 1${\$displaystyle {\binom {t}{0}} = 1}이라는 사실과 용어를 재배열하면,

${\displaystyle 1={\binom {t}{1}}-{\binom {t}{2}}+\cdots +(-1)^{t+1}{\binom {t}{t}},}$

따라서 선택된 요소는 식 (1)의 오른쪽에 의해 한 번만 계산됩니다.

대수적 증명

대수적 증명은 지표 함수(특성 함수라고도 함)를 사용하여 얻을 수 있습니다. 집합 X의 부분집합 S의 지시함수는

${\displaystyle {\begin{aligned}&\mathbf {1} _{S:X\to \{0,1\}\\&\mathbf {1} _{S}(x)={\begin{case}1&x\in S\0&x\notin S\end{case}}\end{aligned}}$

$A{\displaystyle }$ ${\displaystyle A}$와 $B{\displaystyle }$ ${\displaystyle$ B$}$가 $X{\displaystyle }$ ${\displaystyle$ X$}$의 두 부분집합이라면$,$

${\displaystyle \mathbf {1} _{A}\cdot \mathbf {1} _{B}=\mathbf {1} _{A\cap B}}$

$\underset{}{\overset{}{결합}}$ ⋃ $i_{}$ = 1 $n$ Ai {\textstyle \bigcup _{i=1}^{n}라고 하자.집합₁ A, …, A의_n $A_{i}}.$ 일반적으로 포함-배제 원리를 증명하기 위해, 우리는 먼저 아이덴티티를 검증합니다.

${\displaystyle \mathbf {1} _{A}=\sum _{k=1}^{n}(-1)^{k-1}\sum _{I\subset \{1,\ldots ,n\} \atop I =k}\mathbf {1} _{A_{I}}}$

(⁎)

표시기 기능의 경우 다음과 같습니다.

${\displaystyle A_{I}=\bigcap _{i\in I}A_{i}.}$

다음 함수

${\displaystyle \left(\mathbf {1}_{A}-\mathbf {1}_{A_{1}}\right)\left(\mathbf {1}_{A}-\mathbf {1}_{A_{2}\right)\cdots \left(\mathbf {1}_{A}-\mathbf {1}_{A_{n}\right),}$

x가 A에 속하지 않으면 모든 인자는 0 - 0 = 0 이고, 그렇지 않으면 x가 어떤 A에 속하면 대응하는 m 인자는 1 - 1 = 0 이 됩니다. 좌변에 곱을 펼치면 식 (⁎)는 다음과 같습니다.

집합의 기수에 대한 포함-배제 원리를 증명하기 위해 A, …, A의 결합에서 모든 x에 대한 방정식(⁎)을 합합니다. 확률에 사용되는 버전을 도출하려면 (⁎)의 기대를 사용합니다. 일반적으로 방정식(⁎)을 μ에 대해 적분합니다. 이러한 유도에는 항상 선형성을 사용합니다.

참고 항목

• 부울의 부등식 – 확률 공간에 적용되는 부등식
• 조합 원리 – 조합론에서 사용되는 방법
• Maximum-minimums identity – 숫자 집합의 최대값과 비어 있지 않은 부분 집합의 최소값을 연관시킵니다.
• 목걸이 문제
• 비둘기 구멍 원리 – 상자가 들어 있는 것보다 더 많은 품목이 있는 경우, 한 상자에 적어도 두 개 이상의 품목이 들어 있어야 합니다.
• Schuette–Nesbit 공식 – 확률 이론의 수학 공식 - 위키데이터 설명을 폴백으로 표시하는 페이지

메모들

참고문헌

• Allenby, R.B.J.T.; Slomson, Alan (2010), How to Count: An Introduction to Combinatorics, Discrete Mathematics and Its Applications (2 ed.), CRC Press, pp. 51–60, ISBN 9781420082609
• Björklund, A.; Husfeldt, T.; Koivisto, M. (2009), "Set partitioning via inclusion–exclusion", SIAM Journal on Computing, 39 (2): 546–563, doi:10.1137/070683933
• Brualdi, Richard A. (2010), Introductory Combinatorics (5th ed.), Prentice–Hall, ISBN 9780136020400
• Cameron, Peter J. (1994), Combinatorics: Topics, Techniques, Algorithms, Cambridge University Press, ISBN 0-521-45761-0
• Fernández, Roberto; Fröhlich, Jürg; Alan D., Sokal (1992), Random Walks, Critical Phenomena, and Triviality in Quantum Field Theory, Texts an Monographs in Physics, Berlin: Springer-Verlag, pp. xviii+444, ISBN 3-540-54358-9, MR 1219313, Zbl 0761.60061
• Graham, R.L.; Grötschel, M.; Lovász, L. (1995), Hand Book of Combinatorics (volume-2), MIT Press – North Holland, ISBN 9780262071710
• Gross, Jonathan L. (2008), Combinatorial Methods with Computer Applications, Chapman&Hall/CRC, ISBN 9781584887430
• "Inclusion-and-exclusion principle", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Mazur, David R. (2010), Combinatorics A Guided Tour, The Mathematical Association of America, ISBN 9780883857625
• Roberts, Fred S.; Tesman, Barry (2009), Applied Combinatorics (2nd ed.), CRC Press, ISBN 9781420099829
• Stanley, Richard P. (1986), Enumerative Combinatorics Volume I, Wadsworth & Brooks/Cole, ISBN 0534065465
• van Lint, J.H.; Wilson, R.M. (1992), A Course in Combinatorics, Cambridge University Press, ISBN 0521422604

이 문서는 PlanetMath의 포함 배제 원칙의 자료를 통합하고 있으며, 이 자료는 Creative Commons Attribution/Share-Alike License에 따라 라이센스가 부여되어 있습니다.