Ω-autom톤

이론 컴퓨터 과학의 한 분야인 오토마타 이론에서 Ω-오토마톤(또는 스트림 오토마톤)은 입력으로서 유한한 문자열이 아닌 무한히 무한하게 실행되는 유한 오토마타의 변형이다.Ω-automata는 멈추지 않기 때문에 단순히 수용 상태의 집합보다는 다양한 수용 조건을 가지고 있다.

Ω-automata는 하드웨어, 운영 체제, 제어 시스템과 같이 종료할 것으로 예상되지 않는 시스템의 동작을 지정하는 데 유용하다.그러한 시스템의 경우, "모든 요청에 대해, 결국 승인이 뒤따른다" 또는 "인정이 뒤따르지 않는 요청이 있다"와 같은 속성을 명시하기를 원할 수 있다.전자는 무한한 말의 속성이다. 즉, 이 속성을 만족한다는 유한한 순서를 말할 수 없다.

Ω-automata의 등급은 각각 결정론적 또는 비결정론적인 Büchi automata, Rabin automata, Streett automata, parity automata, Muller aomata를 포함한다.이러한 Ω-automata의 등급은 수용 조건에서만 다르다.그들은 결정론적인 Büchi automata를 제외하고 모두 정규 Ω 언어를 정확하게 인식하고 있는데, 이는 다른 모든 언어보다 엄격히 약하다.이러한 모든 유형의 오토마타는 동일한 Ω 언어 집합을 인식하지만, 그럼에도 불구하고 주어진 Ω 언어에 대한 표현 간명성은 다르다.

결정론 Ω-오토마타

형식적으로 결정론 Ω-automaton은 튜플 A = (Q,ENT,Δ,Q₀,Ac)로서 다음과 같은 성분으로 구성된다.

• Q는 유한한 집합이다.Q의 원소를 A의 상태라고 한다.
• σ은 A의 알파벳이라 불리는 유한 집합이다.
• Δ: Q × σ → Q는 A의 전이함수라 불리는 함수다.
• Q는₀ Q의 요소로서 초기 상태라고 한다.
• Acc는 승인 조건이며, 공식적으로 Q의^ω 하위 집합이다.

A에 대한 입력은 알파벳 σ에 대한 무한 문자열이다. 즉, 무한 시퀀스 α = (a₁₂,a₃,a,a,...)이다.그러한 입력에 대한 A의 런은 다음과 같이 정의된 상태의 무한 시퀀스 ρ = (r₀,r₁,r₂,r,...)이다.

• r₀ = q₀.
• r₁ = Δ(r₀,a₁)
• r₂ = Δ(r₁,a₂)

...

• r_n = Δ(r_n-1,a_n)

Ω-automaton의 주요 목적은 모든 입력 집합의 하위 집합을 정의하는 것이다.허용되는 입력 집합.반면에, 일반적인 유한 자동화의 경우, 모든 실행은 상태_n r로 끝나고, r이_n 수용 상태인 경우에만 입력이 허용되지만, Ω-automata에 대해서는 허용 입력 집합의 정의가 더 복잡하다.여기서 우리는 전체 런 ρ을 살펴봐야 한다.해당 실행이 Acc에 있을 경우 입력이 허용된다.수용된 입력 Ω-words 집합은 자동자에 의해 인식된 Ω 언어라고 불리며, 이를 L(A)로 나타낸다.

Q의^ω 하위 집합으로서 Acc의 정의는 순전히 형식적이며 일반적으로 그러한 집합은 무한하기 때문에 연습에 적합하지 않다.다양한 종류의 Ω-automata(부치, 라빈 등) 사이의 차이는 Q의^ω 특정 하위 집합 Acc를 유한 집합으로 인코딩하는 방법에 있으며, 따라서 그러한 하위 집합이 인코딩할 수 있는 방법에 있다.

비결정성 Ω-오토마타

형식적으로 비결정성 Ω-automaton은 튜플 A = (Q,ENT,Δ,Q₀,Ac)로서 다음과 같은 성분으로 구성된다.

• Q는 유한한 집합이다.Q의 원소를 A의 상태라고 한다.
• σ은 A의 알파벳이라 불리는 유한 집합이다.
• Δ는 Q × × × Q의 부분집합으로 A의 전이관계라고 한다.
• Q는₀ Q의 하위 집합으로, 초기 상태 집합이라고 불린다.
• Acc는 Q의^ω 부분집합인 허용 조건이다.

전환 함수 Δ를 갖는 결정론 Ω-automaton과 달리, 비결정론적 버전은 전환 관계 Δ를 가진다.Δ는 함수로서 간주될 수 있다는 점에 유의한다 : Q × σ → P(Q) × σ에서 전력 집합 P(Q)까지의 함수.따라서 상태 q와_n 기호 a를_n 주어진다면, 다음 상태_n+1 q는 반드시 고유하게 결정되는 것이 아니라, 가능한 다음 상태의 집합이 있다.

입력 α = (a₁,a₂,a₃,a,a...)에 대한 A의 런은 다음 조건을 만족하는 임의의 무한 시퀀스 ρ = (r₀,r₁,r₂,r...)이다.

• r은₀ Q의₀ 요소다.
• r은₁ Δ(r₀,a₁)의 원소다.
• r은₂ Δ(r₁,a₂)의 원소다.

...

• r은_n Δ(r_n-1,a_n)의 원소다.

비결정론적 Ω-automaton은 주어진 입력에 대해 많은 다른 런을 허용하거나 전혀 허용하지 않을 수 있다.가능한 실행 중 하나 이상이 수락인 경우 입력이 허용된다.런이 수락되는지 여부는 결정론적 Ω-automata에 관해서 Acc에만 의존한다.모든 결정론 Ω-automaton은 Δ를 Δ의 그래프로 삼음으로써 비결정론 Ω-automaton으로 간주할 수 있다.결정론적 Ω-automata에 대한 런 정의와 합격은 비결정론적 사례의 특별한 경우다.

수용조건

허용 조건은 Ω-words의 무한 집합일 수 있다.그러나 사람들은 대부분 정밀하게 대표할 수 있는 수용 조건을 연구한다.다음은 다양한 대중적 수용 조건을 나열한 것이다.

리스트에 대해 논의하기 전에, 다음과 같이 관찰해 봅시다.무한정 운영되는 시스템의 경우 특정 행동이 무한정 반복되는 경우가 많은지 관심을 갖는 경우가 많다.예를 들어, 네트워크 카드가 무한히 많은 ping 요청을 수신하는 경우, 일부 요청에는 응답하지 못할 수 있지만 수신된 ping 요청의 무한 부분 집합에는 응답해야 한다.이는 다음과 같은 정의에 동기를 부여한다.어떤 런 ρ에 대해서도 Inf(ρ)는 ρ에서 무한히 자주 일어나는 상태 집합이 되게 한다.특정 상태를 무한히 자주 방문한다는 이러한 개념은 다음과 같은 허용 조건을 정의하는 데 도움이 될 것이다.

• Büchi automaton은 Q의 일부 부분집합 F에 대해 다음과 같은 허용 조건을 사용하는 Ω-automaton A이다.

부치 조건

A는 인프(Inf) f F가 비어 있지 않은, 즉 ρ에서 무한히 자주 일어나는 수용 상태가 있는 ρ을 정확히 받아들인다.

• 라빈 자동은 Ω-automaton A로_i, 상태 집합의_i 일부 집합에 대해 다음과 같은 허용 조건을 사용한다.

라빈 조건

A는 Ω으로 쌍(B_i,G_i)이 존재하는 런(Run)을 정확히 받아들여, B_i ∩ Inf(Run)는 비어 있고 G_i ∩ Inf(Run)는 비어 있지 않다.

• A Street automaton은 다음과 같은 허용 조건을 사용하는 Ω-automaton A로, 상태 집합의 일부 설정 Ω(B_i,G_i)에 대해,

스트리트 조건

A는 Ω의 모든_i 쌍(B,G_i)에 대해 B_i ∩ Inf(ρ)가 비어 있거나 G_i ∩ Inf(ρ)가 비어 있지 않은 ρ을 정확히 받아들인다.

• 패리티 자동화는 일부 자연수 k에 대해 상태 집합이 Q = {0,1,2,...,k}이고 다음과 같은 허용 조건을 갖는 자동 A이다.

패리티 조건

A는 Inf(()에서 가장 작은 숫자가 짝수일 경우에만 accepts을 받아들인다.

• Muller automaton은 P(Q)의 부분 집합 F(Q의 전원 집합)에 대해 다음과 같은 허용 조건을 사용하는 Ω-automaton A이다.

뮬러 조건

A는 인프(Inf)가 F의 요소인 ρ의 run을 정확히 받아들인다.

모든 Buchi 자동화는 Muller 자동화로 간주될 수 있다.최소한 F의 요소를 포함하는 Q의 모든 하위 집합으로 구성된 F를 F로 대체하는 것으로 충분하다.마찬가지로 모든 라빈, 스트리트 또는 패리티 오토메이션도 뮬러 오토메이션으로 간주할 수 있다.

예

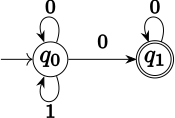
알파벳 σ = {0,1}에 걸쳐 다음과 같은 Ω 언어 L로 비결정론적 Büchi 자동화로 인식할 수 있음: L은 1이 미세하게 여러 번 발생하는 σ의^ω 모든 Ω-words로 구성된다.L을 인식하는 비결정론적 Büchi 자동화는 q₀ (초기 상태)와₁ q. Δ는 3배 (q₀,0,q₀), (q₀₀,q₀), (q₁,0,q₁₁)로 구성된다.F = {q₁}.1이 미세하게 여러 번 발생하는 입력 α의 경우, 읽을 1초가 있는 한 상태 q에₀ 머무른 후 상태 q로₁ 가는 실행이 있다.이번 주행은 성공적이다.1초가 무한히 많은 경우, 가능한 실행은 단 하나, 즉 항상 상태 q에₀ 머무르는 실행이다. (기계가 q를₀ 남기고 q에₁ 도달하면 되돌릴 수 없다.또 다른 1을 읽으면 후계국가가 없다.)

위의 언어는 결정론적 Büchi 자동화로 인식할 수 없다는 점에 유의하십시오. Büchi 자동화는 비결정론적 상대 언어에 비해 표현력이 엄격히 떨어진다.

Ω오토마타의 표현력

유한 문자 σ에 대한 Ω 언어는 σ에 대한 Ω 워드의 집합이다. 즉, σ의^ω 하위 집합이다.σ 이상의 Ω 언어는 Ω-automaton A(동일한 알파벳으로)가 A가 수용하는 모든 Ω-automaton A에 의해 인식된다고 한다.Ω-automata 클래스의 표현력은 클래스 내 일부 자동화로 인식할 수 있는 모든 Ω 언어 클래스에 의해 측정된다.

비결정론적 부치, 패리티, 라빈, 스트리트, 뮬러 오토마타는 모두 정확히 동일한 종류의 Ω-언어를 인식한다.^[1]이것들은 정규 언어의 Ω-Kleene 폐쇄 또는 정규 Ω-언어라고 알려져 있다.다른 증거를 사용하여 결정론적 패리티, 라빈, 스트리트, 뮬러 오토마타 모두 정규 Ω 언어를 인식한다는 것도 보여줄 수 있다.이로부터 정규 Ω 언어의 클래스는 보완 하에 폐쇄된다.그러나 위의 예는 결정론적인 Büchi automata의 등급이 엄격히 약하다는 것을 보여준다.

Ω-automata 사이의 변환

비결정론적 뮬러, 라빈, 스트리트, 패리티, 부치 오토마타 등이 똑같이 표현력이 있기 때문에 서로 번역할 수 있다.Let us use the following abbreviation ${\displaystyle \{N,D\}\times \{M,R,S,P,B\}}$: for example, NB stands for nondeterministic Büchi ω-automaton, while DP stands for deterministic parity ω-automaton.그러면 다음은 붙잡는다.

• 분명히, 결정론적 자동화는 비결정론적 자동화로 볼 수 있다.
• ${\displaystyle N}$ ${\displaystyle B}$→ ${\displaystyle N}$ R${\displaystyle }$/ ${\displaystyle N}$ ${\displaystyle S}$/ ${\displaystyle N}$ ${\displaystyle P}$ ${\displaystyle NB\오른쪽$ 화살표 $NR/NS/NP}($상태 공간에 블로우업 없음$$).
• NR은 상태, 공간에 있는 다항 확대시킨과 함께 → NB{NR\rightarrow NB\displaystyle}, 즉, 주의 결과 주의의 번호는 2nm+주들의 NB에서 n{n\displaystyle}은 번호와 라빈 수락 쌍의 m{m\displaystyle}는 수(예를 들어 보[2])1{2nm+1\displaystyle},.
• ${\displaystyle N}$ ${\displaystyle S}$/ ${\displaystyle N}$ ${\displaystyle M}$/ N ${\displaystyle P}$→ ${\displaystyle N}$ ${\displaystyle B}$ ${\displaystyle NS/NM/NP\rightarrow NB}$ 상태 공간에서 지수적인 블로업이 발생하는$$ 경우.
• ${\displaystyle \mathrm{상태}}$ 공간에서 지수적인 블로업이 있는$$ N B${\displaystyle }$→ D ${\displaystyle R}$/ ${\displaystyle D}$ ${\displaystyle P}$ ${\displaystyle NB\오른쪽$ 화살표 $DR/DP}$이 결정 결과는 Safra의 건설을 이용한다.

번역에 대한 포괄적인 개요는 참조된 웹 소스에서 찾을 수 있다.^[3]

추가 읽기

• Farwer, Berndt (2002), "ω-Automata", in Grädel, Erich; Thomas, Wolfgang; Wilke, Thomas (eds.), Automata, Logics, and Infinite Games, Lecture Notes in Computer Science, Springer, pp. 3–21, ISBN 978-3-540-00388-5.
• Perrin, Dominique; Pin, Jean-Éric (2004), Infinite Words: Automata, Semigroups, Logic and Games, Elsevier, ISBN 978-0-12-532111-2
• Thomas, Wolfgang (1990), "Automata on infinite objects", in van Leeuwen, Jan (ed.), Handbook of Theoretical Computer Science, vol. B, MIT Press, pp. 133–191, ISBN 978-0-262-22039-2
• Bakhadyr Khoussainov; Anil Nerode (6 December 2012). Automata Theory and its Applications. Springer Science & Business Media. ISBN 978-1-4612-0171-7.

참조