사다리꼴

이중 통일 n-곤 사다리꼴 헤드라 세트
이중 통일 오각형 사다리꼴 예
유형	이중관절 다면체의 의미에서의 이중관절
콘웨이 표기법	dan
슐레플리 기호	{ } ⨁ {n}[1]
콕시터 도표
얼굴	연 2n
가장자리	4n
정점	2n + 2
면 구성	V3.3.3.n
대칭군	Dnd, [2+,2n], (2*n), 주문 4n
회전군	Dn, [2,n],+ (22n), 주문 2n
이중 다면체	(convex) 균일한 n-곤 항정신병
특성.	볼록한, 얼굴-변형, 정점[2]

n-곤 사다리꼴, 안티피라미드, 안티피라미드 또는 델토헤드론은 n-곤 항정신병증의 이중 다면체다. n-트래피조헤드론의 2n 얼굴은 합치되고 대칭적으로 엇갈려 있다; 그것들은 꼬인 연이라고 불린다. 대칭이 더 높은 그것의 2n 얼굴은 연이다.^{[citation needed]}

이름의 n-곤 부분은 여기서 면들을 가리키는 것이 아니라 n-폴드 대칭의 축을 중심으로 각 n 정점의 두 배열을 가리킨다. 이중 n-곤 항정신병증에는 실제 n-곤 얼굴 두 개가 있다.

n-곤 사다리꼴은 두 개의 동일한 n-곤 피라미드와 n-곤 항정신병증으로 해부될 수 있다.

이름

델토헤드라라고도 불리는 이 수치들은 얼굴이 정삼각형인 델타헤드라와 혼동해서는 안 된다.

뒤틀린 삼각형 사다리꼴(6개의 뒤틀린 사다리꼴 면)과 뒤틀린 사다리꼴(8개의 뒤틀린 사다리꼴 면)은 결정체로 존재한다. 결정학에서는^[3] 사다리꼴과 사다리꼴이라고 부른다. 그들은 대칭면도 없고, 대칭 중심도 없다. 삼각 사다리꼴은 3배 대칭 축이 하나 있으며, 2배 대칭 축 3개에 수직이다.^[4] 4각형 사다리꼴은 하나의 4배 대칭 축을 가지며, 4배 대칭 축은 4배 대칭 축에 수직이다.^[4]

또한 결정학에서도 사다리꼴이라는 단어는 사다리꼴 얼굴이 24개인 다면체에 (달성) 이코시테트라헤드론이라고 적절하게 알려져 있는 경우가 많다.^[5] 12개의 사다리꼴 얼굴을 가진 또 다른 다면체는 델토이드 도데면체로 알려져 있다.^[6]

대칭

n-곤 사다리꼴 사다리꼴의 대칭 그룹은 순서가 4n인_nd D로, n = 3: 입방체의 경우 순서가 48 = 4×(4×3)인 대칭 그룹 O가_d 크며, D의_3d 네 가지 버전이 하위 그룹으로 지정된다.

n-트라페조헤드론의 회전 그룹은 순서 2n의 D로_n, n = 3: 입방체의 경우 순서가 24 = 4×(2×3)인 큰 회전 그룹 O를 가지며, 부분군으로 D의₃ 네 가지 버전이 있다.

자유의 대칭에 Dnd(주문 4n)Dn(주문 2n)에서 어느 정도 왜곡된 연을 드리고 주 n-trapezohedron 트라페조헤 드론이라 불린다.(그 한계에서, 각각의 네 변의 한쪽 가장자리 0길이도 그리고는 n-trapezohedron이 되는 n-bipyram은 합동 3가장자리를 합동 quadrilaterals에 kites을 바꾼다.이드라는 것이다.)

만약 두 봉우리를 둘러싸고 있는 연이 꼬이지 않고 두 개의 다른 모양을 하고 있다면, n-트라페조헤드론은 C_nv(수직 거울로 순환) 대칭만 가질 수 있고 순서 2n을 가질 수 있으며, 불평등하거나 비대칭적인 사다리헤드론이라고 불린다. 그것의 이중성은 서로 다른 반경의 상단과 하단의 다각형을 가진 불평등한 n-반티프리즘이다.

연이 꼬여 있고 두 가지 모양이 다른 경우, n-트라페조헤드론은 C_n(순환) 대칭, 순서 n만 가질 수 있으며, 불평등한 꼬임 사다리꼴이라고 불린다.

육각형 사다리꼴을 사용한 변동의 예(n = 6)

사다리꼴형	트위스트 사다리꼴		불평등 사다리꼴	불평등 트위스트 사다리꼴
대칭군	D6, (662), [6,2]+		C6v, (*66), [6]	C6, (66), [6]+
다면체 이미지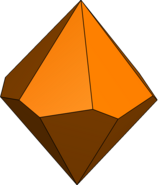
그물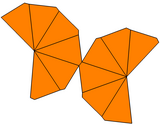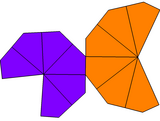

양식

n-트라페조헤드론은 2n 4각형 면과 2n+2 정점을 가지고 있다. 두 개의 꼭지점이 극축에 있고, 다른 꼭지점은 정점의 두 개의 규칙적인 n-곤 링에 있다.

n-곤 사다리꼴 헤드라 계열

사다리꼴 이름	디지온 사다리꼴 (테트라헤드론)	삼각 사다리꼴	사방형 사다리꼴	오각형 사다리꼴	육각 사다리꼴	십각형 사다리꼴	팔각사다리꼴	십각형 사다리꼴	도십각형 사다리꼴	...	아페이로겐 사다리꼴
다면체 이미지										...
구형 타일링 영상										평면 타일링 영상
면 구성	V2.3.3.3	V3.3.3.3	V4.3.3.3	V5.3.3.3	V6.3.3.3	V7.3.3.3	V8.3.3.3	V10.3.3.3	V12.3.3.3	...	V∞.3.3.3

특별한 경우:

• n = 2. 사다리꼴의 퇴행형: 정점이 6개, 가장자리가 8개, 연면이 4개 있는 기하학적 사면체로서 삼각형으로 퇴행한다. 그것의 이중성은 퇴화된 형태의 항정신병이다. 또한 사면체다.
• n = 3. 삼각형 항정신병증의 이중: 연은 rhombi(또는 사각형)이다. 따라서 이러한 사다리꼴도 역시 조노헤드라(zonoheedra)이다. 그것들은 Rhomboedra라고 불린다. 그것들은 몸체의 대각선 방향으로 정육면체 크기로 되어 있다. 그것들은 또한 응고된 rhombic 얼굴을 가진 평행한 종이다.
  

  60° 회전수(Rhombohedron)로, 중앙 정규 팔면체와 두 개의 정규 사면체로 해부되었다.
  • 코롬면체의 특별한 경우는 얼굴을 형성하는 코롬비의 각도가 60°와 120°인 경우다. 그것은 두 개의 동일한 정규 4면체와 일반 8면체로 분해될 수 있다. Parallelelephipeds는 공간을 채울 수 있기 때문에, 정규 4면체와 일반 8면체의 조합도 채울 수면을 채울 수 있다.

예

• 원자의 결정 배열은 삼각형 및 육각형 사다리꼴 세포로 우주에서 반복될 수 있다.^[7]
• 오각형 사다리꼴은 던전앤드래곤과 같은 롤플레잉 게임에서 다이(Die)로 흔히 쓰이는 플라토닉 고형물 외에 유일한 다면체다면체다. 10개의 면을 가지고 있기 때문에, 그것은 원하는 십진수 기반의 균일 확률을 생성하기 위해 반복적으로 사용될 수 있다. 00부터 99까지의 숫자를 나타내기 위해 일반적으로 다른 색의 주사위 2개가 사용된다.

별사다리꼴

얼굴-변환성 별 p/q-trapezohedron은 지그재그 스큐 별 2p/q-gon 베이스로 정의되며, 두 개의 대칭 에이펙스(자유도가 없는 두 개의 대칭 에이펙스)는 베이스 가장자리의 각 쌍을 하나의 에이펙스에 연결한다.

그러한 별 p/q 트라페조헤드론은 자가 교배형, 교차형 또는 비콘벡스형이다. It exists for any regular zig-zag skew star 2p/q-gon base; but if p/q < 3/2, then p — q < q/2, so the dual star antiprism (of the star trapezohedron) cannot be uniform (i.e.: cannot have equal edge lengths); and if p/q = 3/2, then p — q = q/2, so the dual star antiprism must be flat, thus degenerate, to be uniform.

이중 통일 별 p/q-트라페조헤드론에는 Coxeter-Dynkin 도표가 있다.

최대 p = 12까지의 이중 통일 별 p/q-트라페조헤드라

5/2	5/3	7/2	7/3	7/4	8/3	8/5	9/2	9/4	9/5

10/3	11/2	11/3	11/4	11/5	11/6	11/7	12/5	12/7

도십각형 사다리꼴

도각형 사다리꼴은 24개의 연을 가진 사다리꼴이다. 12배 반격자 대칭, 순서 48이다.

참고 항목

위키미디어 커먼즈에는 트라페조헤드라 관련 미디어가 있다.

• 사다리꼴 감소
• 롬빅 도데카헤드론
• 롬빅 삼권면체
• 비피라미드
• 잘린 사다리꼴
• 콘웨이 다면체 표기법
• H.P. Lovecraft의 단편 소설 "The Shining Trapezoheedron"으로 알려진 가상의 고대 유물이 결정적인 역할을 하는 "The Hunter of the Dark"이다.

참조

• Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. 제4장: 아르키메데스 다면체, 프리즘, 반격체의 이중체
• Spencer, Leonard James (1911). "Crystallography" . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 07 (11th ed.). Cambridge University Press. pp. 569–591.

외부 링크

• Weisstein, Eric W. "Trapezohedron". MathWorld.
• Weisstein, Eric W. "Isohedron". MathWorld.
• 가상현실 폴리헤드라 폴리헤드라 백과사전
  • VRML 모델(George Hart) <3> <4> <5> <6> <7> <9> <10>
  • Polyedra Try에 대한 Conway 표기법: "DAn", 여기서 n=3,4,5... 예: "dA5"는 오각형 사다리꼴이다.
• 종이 모델 4각형(사각형) 사다리꼴