와이토프 기호
Wythoff symbol기하학에서 Wythoff 기호는 슈바르츠 삼각형 내에 균일한 다면체 또는 평면 타일링의 Wythoff 구문을 나타내는 표기법이다. 그것은 콕시터, 롱구엣 히긴스, 밀러에 의해 균일한 다면체의 열거에 처음 사용되었다. 후에 Coxeter 도표는 기본 심플렉스 내의 n차원 공간에 균일한 폴리토페스와 허니콤을 표시하도록 개발되었다.
와이토프 기호는 세 개의 숫자와 세로 막대로 구성된다. 동일한 타일링/다면체는 다른 대칭 생성기와 다른 Wythoff 기호를 가질 수 있지만, 하나의 균일한 다면체 또는 타일링을 나타낸다. 예를 들어 정규 입방체는 Oh 대칭으로 3 2 4를, 2 4 2를 2색 대칭으로4h 사각 프리즘으로, 2 4 2를 3색 대칭으로2h 나타낼 수 있다.
약간의 연장만 있으면 와이토프의 기호를 모든 균일한 다면체에 적용할 수 있다. 그러나 이 공사방법이 유클리드나 쌍곡선 공간에 모든 균일한 기울기로 이어지는 것은 아니다.
설명
와이토프 건설은 기본 삼각형의 발전기 점을 선택하는 것으로 시작한다. 각 측면으로부터 이 점의 거리가 0이 아닌 경우, 각 가장자리로부터 동일한 거리로 점을 선택해야 한다. 그런 다음 수직선은 발전기 지점과 그것이 놓여 있지 않은 모든 면 사이에 떨어지게 된다.
와이토프의 상징인 p, q, r에 있는 세 숫자는 공사에 사용된 슈바르츠 삼각형의 모서리를 나타내며, 이 세 개의 숫자는 이 공사에 사용된 슈바르츠 삼각형의 모서리를 나타낸다. π/p, π/q, π/rradians. 삼각형도 같은 숫자로 표기되어 있다(pqr). 기호의 수직 막대는 다음과 같이 기본 삼각형 내에 있는 발전기 점의 범주형 위치를 지정한다.
- p q r은 발전기가 코너 p에 놓여 있음을 나타낸다.
- p q r은 발전기가 p와 q 사이의 가장자리에 있음을 나타낸다.
- p q r은 발전기가 삼각형의 내부에 있음을 나타낸다.
이 표기법에서 거울은 반대 정점의 반사 순서에 의해 라벨이 붙는다. 해당 미러가 활성 상태일 경우 p, q, r 값이 막대 앞에 나열된다.
특수 용도는 모든 거울이 활성 상태지만 홀수 숫자 반사 이미지는 무시되는 경우에 대해 지정된 기호 p q r이다. 결과 수치는 회전 대칭만 가진다.
제너레이터 지점은 각 미러를 켜거나 끌 수 있으며, 활성화되거나 비활성화될 수 있다. 이러한 구별은 모든 미러에 제너레이터 포인트가 있는 위치를 무시한 채 8개의3 가능한 형태를 만든다.
Wythoff 기호는 기능적으로 더 일반적인 Coxeter-Dynkin 도표와 유사하며, 각 노드는 거울을 나타내고 그 사이의 호는 숫자로 표시되며 거울 사이의 각도를 나타낸다.(직각도를 나타내는 호는 생략한다) 제너레이터 포인트가 미러에 없을 경우 노드가 동그라미 친다.
오른쪽 삼각형에서 구형, 유클리드 및 쌍곡선 기울기 예제
기본 삼각형은 거울 이미지로 교대로 그려진다. 삼각형(p 3 2)의 순서는 구면(p = 3, 4, 5), 유클리드(p = 6), 쌍곡선(p 7)으로 바뀐다. 쌍곡선 기울기는 푸앵카레 디스크 투영으로 나타난다.
| 와이토프 기호 | q p 2 | 2시 15분 | 2p q | 2p q | p Q 2 | p Q 2 | p Q 2 | p Q 2 |
|---|---|---|---|---|---|---|---|---|
| 콕시터 다이어그램 | ||||||||
| 정점수 | pq | Q.2p.2p | p.q.p.q.q. | 페이지 2q.2q | qp | 페이지 4.4.4 | 4.2p.2q | 3.3.p.3.q. |
| 기금. 삼각형 | 7가지 양식 및 스너브 | |||||||
(4 3 2) | 3 4 2 43 | 2 3 4 3.8.8 | 2 4 3 3.4.3.4 | 2 4 3 4.6.6 | 4 3 2 34 | 4 3 2 3.4.4.4 | 4 3 2  4.6.8 | 4 3 2 3.3.3.3.4 |
(5 3 2) | 3 5 2 53 | 2 3 5 3.10.10 | 2 5 3 3.5.3.5 | 2 5 3 5.6.6 | 5 3 2 35 | 5 3 2 3.4.5.4 | 5 3 2  4.6.10 | 5 3 2 3.3.3.3.5 |
(6 3 2) | 3 6 2 63 | 2 3 6 3.12.12 | 2 6 3 3.6.3.6 | 2 6 3 6.6.6 | 6 3 2 36 | 6 3 2 3.4.6.4 | 6 3 2  4.6.12 | 6 3 2 3.3.3.3.6 |
(7 3 2) | 3 7 2 73 | 2 3 7 3.14.14 | 2 7 3 3.7.3.7 | 2 7 3 7.6.6 | 7 3 2 37 | 7 3 2 3.4.7.4 | 7 3 2  4.6.14 | 7 3 2 3.3.3.3.7 |
(8 3 2) | 3 8 2 83 | 2 3 8 3.16.16 | 2 8 3 3.8.3.8 | 2 8 3 8.6.6 | 8 3 2 38 | 8 3 2 3.4.8.4 | 8 3 2  4.6.16 | 8 3 2 3.3.3.3.8 |
(∞ 3 2) | 3 ∞ 2 ∞3 | 2 3 ∞ 3.∞.∞ | 2 ∞ 3 3.∞.3.∞ | 2 ∞ 3 ∞.6.6 | ∞ 3 2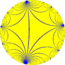 3∞ | ∞ 3 2 3.4.∞.4 | ∞ 3 2  4.6.∞ | ∞ 3 2 3.3.3.3.∞ |
참고 항목
참조
- CoxeterRegular Polytopes, 제3판, (1973) 도버판, ISBN0-486-61480-8 (V장: 칼리도스코프, 섹션: 5.7 와이토프의 건설)
- 콕시터 기하학의 아름다움: 12편의 에세이, 도버 출판사, 1999년 ISBN 0-486-40919-8 (제3장: 균일한 폴리토페스를 위한 와이토프의 건설)
- 콕시터, 롱구엣-하이긴스, 밀러, 제복 다면체, 필 1954년, 246 A, 401–50.
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. 9-10 페이지
외부 링크
- Weisstein, Eric W. "Wythoff symbol". MathWorld.
- 와이토프 기호
- 와이토프 기호
- 와이토프의 공법을 이용해 균일한 폴리에드라(Polyedra)를 표시하는 그렉 이건의 애플릿
- 와이토프 건축공법의 샤데토이 렌더링
- KaleidoTile 3 페이지의 많은 이미지를 생성한 Jeffrey Weeks의 Windows용 무료 교육 소프트웨어.
- Hatch, Don. "Hyperbolic Planar Tessellations".




