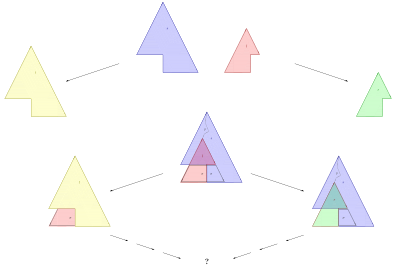크리티컬 페어(용어 개서)

두 개의 개서 규칙 s → t(위 행, 왼쪽) 및 l→r(오른쪽)에서 얻은 임계 쌍의 삼각형 다이어그램입니다.치환 un는 서브텀을 l과 통합합니다.그 결과 얻을 수 있는 오버레이 용어 s[[ l]_p ](하행, 중간)는 각각 용어 t and 및 sσ[ r'_p ](하행, 왼쪽 및 오른쪽)로 고쳐 쓸 수 있습니다.후자의 두 항이 중요한 쌍을 형성합니다.개서 규칙 집합이 합류하는 경우, 최종적으로 공통 용어로 개서할 수 있습니다.

용어 개서 시스템에서는 2개의 개서 규칙이 중복되어 2개의 다른 용어를 생성할 때 중요한 쌍이 발생합니다.보다 자세한 것은, 개서₂ 룰의 2개의 다른 애플리케이션(같은 룰이 다른 경우, 또는 2개의 다른 룰)에₁ 의해서 t 와₂ t 가 생성되는 t 가 존재하는 경우, (t₁, t) 는 중요한 쌍입니다.

정의들

임계 쌍의 실제 정의는 치환에 의해 임계 쌍에서 얻을 수 있는 쌍과 오버랩에 기초한 오리엔테이션 쌍에서 얻을 수 있는 쌍을 제외하기 때문에 약간 더 관련이 있다.구체적으로는 규칙 쌍 $\rho _{0}:l_{0}\to r_{0}$ : $\rho _{0}:l_{0}\to r_{0}$ $\rho _{0}:l_{0}\to r_{0}$ $\rho _{0}:l_{0}\to r_{0}$ 0 { \ $displaystyle$ \ $rho _$ { 0 : $l$ _ { $0$ } \ $to r$ _ $\rho _{0}:l_{0}\to r_{0}$ { 0 $\rho _{0}:l_{0}\to r_{0}$ } $\rho _{1}:l_{1}\to r_{1}$ 1 1 : : $\rho _{1}:l_{1}\to r_{1}$ 1 $\rho _{1}:l_{1}\to r_{1}$ : $l_{1}$ \ $to r_{1$ } $\rho _{1}:l_{1}\to r_{1}$ $l_{0}=D[s]$ being : : $\rho _{1}:l_{1}\to r_{1}$ : $l_{0}=D[s]$ $l_{0}=D[s]$ $l_{0}=D[s]$ { $display$ $\rho _{1}:l_{1}\to r_{1}$ s _ 0 $=$ l _ { 0 } { 0 } $(D\sigma [r_{1}\tau ],r_{0}\sigma )$ { $displaystyle s$ } (변수가 아님)라는 $s$ 는 가장 일반적인 $l_{1}$ $s\sigma =l_{1}\tau$ $=$ $s\sigma =l_{1}\tau$ 1 $s\sigma =l_{1}\tau$ $(D\sigma [r_{1}\tau ],r_{0}\sigma )$ { $displaystyle$ s \ $l _$ $(D\sigma [r_{1}\tau ],r_{0}\sigma )$ { $1$ $s\sigma =l_{1}\tau$ } 、 $(D\sigma [r_{1}\tau ],r_{0}\sigma )$ $(D\sigma [r_{1}\tau ],r_{0}\sigma )$ $displaystyle$ [ $1$ $[$ ( ( ( ( , , 1 1 1 1 11 $(D\sigma [r_{1}\tau ],r_{0}\sigma )$ some some some some1 some some some some1 { displaystyl _ { displaystyle $}$ 과 $l_{1}$ $s\sigma =l_{1}\tau$ $l_{1}$ 합니다.

크리티컬 쌍의 양쪽이 같은 기간으로 축소될 수 있는 경우 크리티컬쌍은 컨버전스라고 불립니다.크리티컬 쌍의 한쪽이 다른 쪽과 동일한 경우 크리티컬쌍은 trivial이라고 불립니다.

예

예를 들어, 규칙을 사용하여 시스템을 다시 쓰는 경우

f(g(x,y),z)	→ g(x,z)
g(x,y)	→ x,

유일하게 중요한 쌍은 'g(x,z)', 'f(x,z)'입니다.이 두 용어 모두 단일 개서 규칙을 적용함으로써 용어 f(g(x,y),z)에서 도출할 수 있습니다.

또 다른 예로는 단일 규칙을 사용하여 시스템을 다시 쓴다는 용어를 생각해 보십시오.

f(x,y)

→ x.

이 규칙을 f(f(x,x),x)라는 용어에 두 가지 다른 방법으로 적용함으로써 (f(x,x), f(x,x)가 (중요한) 중요한 쌍임을 알 수 있습니다.

중요 쌍 보조 규칙

컨버전스란 수렴 크리티컬쌍을 명확하게 의미합니다.크리티컬쌍 'a, b' 중 하나가 발생하면 a와 b는 공통의 리덕션을 가지기 때문에 크리티컬쌍은 컨버전스 됩니다.rewrite system이라는 용어가 convergence가 아닌 경우 critical pair는 convergence가 되지 않을 수 있으므로 critical pair는 convergence가 실패할 가능성이 있습니다.

크리티컬 쌍에 대한 설명은 모든 크리티컬 쌍이 수렴하는 경우에만 용어 재작성 시스템이 약하게(로컬로) 수렴된다는 것을 나타냅니다.따라서 용어 재작성 시스템이 약하게 합치하고 있는지 여부를 확인하려면 모든 중요한 쌍을 테스트하고 수렴 여부를 확인하는 것으로 충분합니다.이것에 의해, 2개의 항이 수렴하는지를 알고리즘으로 확인할 수 있기 때문에, 용어 개서 시스템이 약하게 융합하고 있는지 아닌지를 알고리즘으로 확인할 수 있다.

「」를 참조해 주세요.

Knuth-Bendix 완료, 주어진 것과 동등한 합류 및 종단 용어 재작성 시스템을 계산하기 위한 중요한 쌍을 기반으로 하는 알고리즘

외부 링크

Weisstein, Eric W. "Critical Pair". MathWorld.

레퍼런스

^ Terese (2003). Term rewriting systems. Cambridge, UK: Cambridge University Press. p. 53. ISBN 0-521-39115-6.

Franz Baader and Tobias Nipkow, 용어 변경 및 모든 것, 케임브리지 대학 출판부, 1998년(도서 웹 링크)

[1] Terese (2003). Term rewriting systems. Cambridge, UK: Cambridge University Press. p. 53. ISBN 0-521-39115-6.

Search

크리티컬 페어(용어 개서)

네임스페이스

더

목차

정의들

예

중요 쌍 보조 규칙

「」를 참조해 주세요.

외부 링크

레퍼런스

Search

크리티컬 페어(용어 개서)

정의들

예

중요 쌍 보조 규칙

「 」를 참조해 주세요.

외부 링크

레퍼런스

「」를 참조해 주세요.