각도 결함

기하학에서 (사각형) 결점(또는 결점 또는 결점)은 유클리드 평면의 그러한 각도가 예상되는 360° 또는 180°의 양까지 더해지는 일부 각도의 고장을 의미한다.반대 개념은 과잉이다.

일반적으로 결함은 두 가지 방법으로 발생한다.

• 다면체의 정점 결함
• 쌍곡선 삼각형의 결함

초과분은 다음과 같은 두 가지 방법으로 발생한다.

• 토로이드 다면체의 초과
• 구형 삼각형의 초과

유클리드 평면에서, 한 점에 대한 각도는 360°까지 더해지는 반면, 삼각형의 내부 각도는 180°까지 더해진다(동등하게, 외부 각도는 360°까지 더해진다).그러나 볼록한 다면체에서 정점의 각도는 360° 미만으로, 구형 삼각형에서는 내부 각도는 항상 180° 이상, 쌍곡선 삼각형의 각도는 항상 180° 미만(외부 각도는 360° 미만으로), 쌍곡선 삼각형의 각도는 항상 180° 미만으로 증가한다(외부 각도는 360° 이상).

현대적인 관점에서, 정점이나 삼각형 이상의 결점(마이너스)은 가우스-보넷 정리에 의해 확립된 바와 같이 정확하게 그 지점의 곡률 또는 삼각형 위의 총(통합)이다.

정점의 결함

다면체의 경우, 정점에서의 결함은 정점에 있는 모든 각도의 합을 뺀 2㎛와 같다(정점에 있는 모든 면이 포함됨).다면체가 볼록한 경우 각 정점의 결점은 항상 양수다.만약 각도의 합이 비콘벡스 다면체의 일부 정점들에서 일어나는 것과 같이 완전한 회전을 초과한다면, 결점은 음이다.

결함의 개념은 최고점에 있는 세포의 이음각의 합이 완전한 원에 미치지 못하는 양에 따라 더 높은 차원으로 확장된다.

예

일반 도데카헤드론(각 꼭지점에서 3개의 정규 5각형이 만나는 곳)의 정점 중 어떤 것의 결함은 36°, 즉 π/5 라디안 또는 원의 1/10이다.각 각도는 108°이다.이들 중 3개는 각 꼭지점에서 만나므로 결함은 360°(108° + 108° + 108°)이다.= 36°.

다른 플라토닉 고형분에 대해서도 동일한 절차를 따를 수 있다.

모양	정점 수	각 꼭지점에서 만나는 다각형	각 꼭지점의 결점	총불량
사면체	4	정삼각형 3개	${\displaystyle \pi \ (180^{\filency }}}$	$\\displaystyle 4\pi \ ( \^{\pi \}})}$
팔면체	6	정삼각형 4개	${\displaystyle {2\pi \over 3}\ (120^{\pi }})$	$\\displaystyle 4\pi \ ( \^{\pi \}})}$
정육면체	8	세 칸	${\displaystyle {\pi \over 2}\ (90^{\pi \over }})}$	$\\displaystyle 4\pi \ ( \^{\pi \}})}$
이코사헤드론	12	정삼각형 5개	${\displaystyle {\pi \over 3}\ (60^{\pi \over }})}$	$\\displaystyle 4\pi \ ( \^{\pi \}})}$
도데면체	20	일반 펜타곤 3개	${\displaystyle {\pi \over 5}\\ (36^{\pi }}}}}$	$\\displaystyle 4\pi \ ( \^{\pi \}})}$

데카르트의 정리

다면체의 "총결함"에 대한 데카르트의 정리는 다면체가 구체(즉, 표면학적으로 구와 동등하여 찢지 않고 늘어나 구로 변형될 수 있음)에 대해 동형인 경우, "총결함", 즉 정점 전체의 결함의 합은 두 개의 완전한 원(또는 720° 또는 4㎛ 라디안)이라고 명시하고 있다.다면체는 볼록할 필요가 없다.^[1]

총결함에서 원의 수는 다면체의 오일러 특성과 동일하다고 일반화는 말한다.이것은 가우스 곡률의 적분을 오일러 특성과 연관시키는 가우스-보넷 정리의 특별한 경우다.여기서 가우스 곡면성은 정점에 집중된다: 얼굴과 가장자리에서는 가우스 곡면성이 0이고 정점에서 가우스 곡면성의 적분은 그곳의 결점과 같다.

이는 모든 면의 각도를 합산하고 총 결점을 추가하여 다면체의 정점수 V를 계산하는 데 사용할 수 있다.이 총계는 다면체의 모든 정점에 대해 하나의 완전한 원을 가질 것이다.다면체에 올바른 오일러 특성을 사용할 수 있도록 주의해야 한다.

이 정리와의 역은 알렉산드로프의 고유성 정리에 의해 주어지는데, 이에 따라 4㎛에 이르는 양의 각결함의 한정된 점을 제외한 국소적으로 유클리드인 미터 공간은 볼록한 다면체의 표면으로서 독특한 방법으로 실현될 수 있다.

비콘벡스 수치에 대한 양의 결함

모든 비콘벡스 다면체는 결함이 음의 정점을 가지고 있어야 한다고 생각하는 것은 유혹적이지만, 이것은 그럴 필요가 없다.이것에 대한 두 개의 백배는 각각 양성 결함을 가진 12개의 볼록점을 가진 작은 도마뱀과 큰 도마뱀이다.

양성 결점이 있는 폴리헤드라

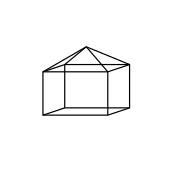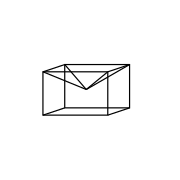스스로 교차하지 않는 백색샘플은 한 면이 정사각형 피라미드로 대체되는 큐브에 의해 제공된다: 이 길쭉한 사각 피라미드는 볼록하고 각 정점의 결점은 각각 양이다.이제 네모난 피라미드가 큐브 안으로 들어가는 동일한 큐브를 생각해 보십시오. 이것은 오목하지만 결점은 그대로 유지되고 모든 것이 양성이 된다.

음의 결함은 정점이 안장점과 닮았다는 것을 의미하지만, 양의 결함은 정점이 국소 최대치 또는 최소치와 닮았다는 것을 의미한다.

참조

메모들

참고 문헌 목록

• 리치슨, D.; 오일러의 보석: 다면체 공식과 위상의 탄생, 프린스턴(2008) 220-225페이지.

외부 링크

무료 사전인 Wiktionary에서 결점을 찾아 보십시오.

• Weisstein, Eric W. "Angular defect". MathWorld.