최후의 날 규칙

존 콘웨이, 2020년 15번째 운명의 날에 죽은 둠스데이 알고리즘의 발명가

Doomsday 규칙은 주어진 날짜에 대한 요일을 결정하는 알고리즘이다. 그것은 그레고리력으로 400년 주기로 움직이기 때문에 영구적인 달력을 제공한다. 정신적 계산을 위한 알고리즘은 1973년 존 콘웨이에 의해 고안되어 루이스 캐럴의 영구적인 달력 알고리즘에서 영감을 얻었다.^[1]^[2]^[3]^[4]^[5] 그것은 매년 기억하기 쉬운 특정한 날짜, 즉 2월 마지막 날, 4/4, 6/6, 8/8, 10/10, 12/12가 어느 해의 같은 날에 발생하는 특정 요일을 이용한다. Doomsday 알고리즘을 적용하려면 다음 세 단계를 수행하십시오. 세기별 앵커데이 결정, 세기별 앵커데이 계산, 종말일(예: 4/4와 6/6)에 항상 해당하는 날짜 중 가장 가까운 날짜 선택, 해당 날짜와 해당 요일 사이의 일수(modulo 7) 카운트. 이 기법은 양력 달력과 율리우스 달력에 모두 적용되지만, 종말일은 보통 요일이 다르다.

알고리즘은 정신적으로 계산할 수 있을 정도로 간단하다. 콘웨이는 보통 2초 안에 정답을 맞출 수 있었다. 속도를 높이기 위해 그는 컴퓨터에 달력 계산을 연습했는데, 이 계산은 로그온할 때마다 무작위 날짜로 퀴즈를 내도록 프로그램되어 있었다.^[6]

근현대 몇 년 동안의 앵커 데이

양력(2022년)의 현재 연도의 닻날은 월요일이다. 다른 현대적 연도의 경우:

**양력 기준일**
Mon.	Tue.	Wed.	Thu.	Fri.	Sat.	Sun.
1898	1899	1900	1901	1902	1903	→
1904	1905	1906	1907	→	1908	1909
1910	1911	→	1912	1913	1914	1915
→	1916	1917	1918	1919	→	1920
1921	1922	1923	→	1924	1925	1926
1927	→	1928	1929	1930	1931	→
1932	1933	1934	1935	→	1936	1937
1938	1939	→	1940	1941	1942	1943
→	1944	1945	1946	1947	→	1948
1949	1950	1951	→	1952	1953	1954
1955	→	1956	1957	1958	1959	→
1960	1961	1962	1963	→	1964	1965
1966	1967	→	1968	1969	1970	1971
→	1972	1973	1974	1975	→	1976
1977	1978	1979	→	1980	1981	1982
1983	→	1984	1985	1986	1987	→
1988	1989	1990	1991	→	1992	1993
1994	1995	→	1996	1997	1998	1999
→	2000	2001	2002	2003	→	2004
2005	2006	2007	→	2008	2009	2010
2011	→	2012	2013	2014	2015	→
2016	2017	2018	2019	→	2020	2021
2022	2023	→	2024	2025	2026	2027
→	2028	2029	2030	2031	→	2032
2033	2034	2035	→	2036	2037	2038
2039	→	2040	2041	2042	2043	→
2044	2045	2046	2047	→	2048	2049
2050	2051	→	2052	2053	2054	2055
→	2056	2057	2058	2059	→	2060
2061	2062	2063	→	2064	2065	2066
2067	→	2068	2069	2070	2071	→
2072	2073	2074	2075	→	2076	2077
2078	2079	→	2080	2081	2082	2083
→	2084	2085	2086	2087	→	2088
2089	2090	2091	→	2092	2093	2094
2095	→	2096	2097	2098	2099	2100

그 탁자는 윤년마다 한 칸씩 건너뛰면서 가로로 채워져 있다. 이 표는 100의 배수(예: 1900년과 2100년, 윤년이 아닌 1900년과 2100년)가 아닌 400의 배수(예: 아직 윤년인 2000년)의 양력 연도를 제외하고 28년마다 순환한다. 전체 주기는 율리우스력에서는 28년(1,461주), 그레고리력에서는 400년(20,871주)이다.

항상 운명의 날에 도착하는 기억에 남는 날짜

가까운 종일을 기준점으로 사용하여 주어진 달력 날짜의 요일을 찾을 수 있다. 이를 돕기 위해, 다음은 항상 최후의 날에 착륙하는 매월 기억하기 쉬운 날짜 목록이다.

위에서 언급했듯이, 2월의 마지막 날은 종말을 정의한다. 1월 3일은 평년의 종말일, 1월 4일은 윤년의 종말일로 '4년 중 3번째, 4년 중 4번째'로 기억될 수 있다. 3월이면 사이비 날짜인 3월 1일 전날, 즉 2월 마지막 날을 가리키는 '3월 0일'을 기억할 수 있다.

4월부터 12월까지의 달은 짝수 달로 4/4, 6/6, 8/8, 10/10, 12/12의 두 번 날짜에 포함되며, 모두 종말일에 해당된다. 홀수 월은 "7-11에서 9-5에서 5까지 일한다"라는 니모닉과 함께 기억될 수 있다. 즉, 9/5, 7/11 및 5/9와 11/7은 모두 운수일이다(이는 일/월/일 협약에 모두 적용된다).^[7]

몇몇의 흔한 휴일도 또한 종말이다. 아래 도표는 열거된 출처에서 연상 작용이 적용되는 날짜만 포함한다.

월	기억에 남는 날짜	월/일	니모닉^[8]	전체 일 목록
1월	1월 3일(공통년), 1월 4일(수평년)	1/3 또는 1/4	4년 3년 4년 4년 4년	3, 10, 17, 24, 31 OR 4, 11, 18, 25, 32^[7]
2월	2월 28일(공통년), 2월 29일(수평년)	2/28 또는 2/29	2월의 마지막 날	0, 7, 14, 21, 28 OR 1, 8, 15, 22, 29
3월	"3월 0일" 또는 3월 14일	2014년 3월 3일 또는 3일	"피 데이" 3/14	0, 7, 14, 21, 28
4월	4월 4일	4/4	4/4, 6/6, 8/8, 10/10, 12/12	4, 11, 18, 25, 32
5월	5월 9일	5/9	7-11로 9 대 5	2, 9, 16, 23, 30
6월	6월 6일	6/6	4/4, 6/6, 8/8, 10/10, 12/12	6, 13, 20, 27
7월	7월 11일	7/11	7-11로 9 대 5	4, 11, 18, 25, 32
8월	8월 8일	8/8	4/4, 6/6, 8/8, 10/10, 12/12	1, 8, 15, 22, 29
9월	9월 5일	9/5	7-11로 9 대 5	5, 12, 19, 26
10월	10월 10일	10/10	4/4, 6/6, 8/8, 10/10, 12/12	3, 10, 17, 24, 31
11월	11월 7일	11/7	7-11로 9 대 5	0, 7, 14, 21, 28
12월	12월 12일	12/12	4/4, 6/6, 8/8, 10/10, 12/12	5, 12, 19, 26

특정 연도의 종일은 3월부터 다음 해 2월까지의 기간의 날짜의 평일과 직결되기 때문에, 같은 해의 1월과 2월에는 공통 연도와 윤년을 구분해야 한다.

월	M	둠스데이
얀	1	3/4	C/L	C/D
2월	2	0/1	C/L	C/D
3월	3	7/0	M + 4	C일
5월	5	9
줄리	7	11
9월	9	5	M - 4
11월	11	7
얀	13	9/2		B일
4월	4	4	M	C일
준	6	6
8월	8	8
10월	10	10
12월	12	12
2월	14	13/-1	M - 1	B일

1월과 2월은 전년도의 마지막 두 달로 취급할 수 있다.

예

2021년 크리스마스가 어느 요일인지 알아보려면 다음과 같이 진행하십시오. 2021년도는 일요일이다. 12월 12일은 불운한 날이기 때문에, 그 후 13일(하루 2주)이 지난 12월 25일은 토요일이었다. 크리스마스는 항상 종말 전날이다. 또 7월 4일(미국 독립기념일)은 할로윈(10월 31일), 파이 데이(3월 14일), 복싱 데이(12월 26일)와 마찬가지로 항상 복싱 데이에 있다.

니모닉 평일 이름

Since this algorithm involves treating days of the week like numbers modulo 7, John Conway suggested thinking of the days of the week as "Noneday"; or as "Sansday" (for Sunday), "Oneday", "Twosday", "Treblesday", "Foursday", "Fiveday", and "Six-a-day" in order to recall the number-weekday relation without needing to count them out in one's head.

요일	색인 번호를 붙이다	니모닉
일요일	0	Nonday or 산스데이
월요일	1	어느 날
화요일	2	2일
수요일	3	트레블스데이
목요일	4	포스데이
금요일	5	파이베이
토요일	6	하루 6회

슬라브어, 중국어, 그리스어, 포르투갈어, 갈리시아어, 히브리어와 같은 몇몇 언어가 있는데, 이 언어는 그들의 위치순으로 요일의 이름 중 일부를 기초로 한다. 슬라브어와 중국어는 위의 표에 동의한다; 언급된 다른 언어는 일요일부터 첫 번째 날로 계산된다.

1년 앵커 데이 찾기

세기의 앵커 데이를 먼저 가져라. 종말의 법칙을 위해서, 한 세기는 00년부터 시작해서 99년까지 끝난다. 다음 표는 1800–1899, 1900–1999, 2000–2099 및 2100–2199의 앵커 데이를 보여준다.

세기	앵커데이	니모닉	색인(요일)
1800–1899	금요일	—	5 (파이버데이)
1900–1999	수요일	We-in-disday (대부분의 살아 있는 사람들은 그 세기에 태어났다)	3 (Treblesday)
2000–2099	화요일	Y-Tue-K 또는 Twos-day (Y2K는 금세기 초엽에 있었다)	2 (2일)
2100–2199	일요일	21일은 일요일이다. (2100년은 다음 세기의 시작이다)	0(언젠가)

그레고리력으로 다음 작업을 수행하십시오.

수식

5 \times

(

c

mod

4

) mod 7

+ 화요일 = 닻.

알고리즘

레트

r

= c

mod

4

r = 0이면 앵커 = 화요일

r = 1이면 앵커 = 일요일

r = 2이면 앵커 = 금요일

r = 3이면 앵커 = 수요일

줄리안 달력의 경우:

6c

mod

7

+ 일요일 = 앵커.

참고:c)⌊.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1pxsolid}.mw.-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}year/100⌋.

다음, 올해의 앵커 데이를 찾아라. Conway에 따라 이를 달성하려면:

연도의 마지막 두 자리수(이 $y$ 를 부름)를 12로 나누고 a를 몫의 바닥이 되게 한다.
$b$ 를 같은 몫의 나머지가 되게 하라.
그 나머지를 4로 $나누고$ c를 몫의 바닥이 되게 하라.
$d$ 를 세 개의 숫자( $d$ = a + b + $c$ )의 합으로 한다. (여기서는 다시 7로 나누고 나머지는 가져가는 것이 가능하다. 이 숫자는 집합적으로 취해진 연도의 마지막 두 자리 숫자와 그 집합 자릿수의 바닥을 4로 나눈 값과 같아야 한다.)
앵커 데이로부터 지정된 $일수$ ( $d 또는$ d/7)를 앞으로 세어 해당 연도 일수를 구한다.

{\begin{matrix}\left({\left\lfloor {\frac {y}{12}}\right\rfloor +y{\bmod {1}}2+\left\lfloor {\frac {y{\bmod {1}}2}{4}}\right\rfloor }\right){\bmod {7}}+{\rm {{anchor}={\rm {Doomsday}}}}\end{matrix}}

예를 들어, 20세기 1966년의 경우:

{\begin{matrix}\left({\left\lfloor {\frac {66}{12}}\right\rfloor +66{\bmod {1}}2+\left\lfloor {\frac {66{\bmod {1}}2}{4}}\right\rfloor }\right){\bmod {7}}+{\rm {Wednesday}}&=&\left(5+6+1\right){\bmod {7}}+{\rm {Wednesday}}\\\ &=&{\rm {Monday}}\end{matrix}}

위의 글머리 기호 4에서 설명한 바와 같이, 이는 다음과 같다.

{\begin{matrix}\left({66+\left\lfloor {\frac {66}{4}}\right\rfloor }\right){\bmod {7}}+{\rm {Wednesday}}&=&\left(66+16\right){\bmod {7}}+{\rm {Wednesday}}\\\ &=&{\rm {Monday}}\end{matrix}}

그래서 1966년의 종말은 월요일에 떨어졌다.

이와 유사하게, 2005년의 종말일은 월요일이다.

\left({\left\lfloor {\frac {5}{12}}\right\rfloor +5{\bmod {1}}2+\left\lfloor {\frac {5{\bmod {1}}2}{4}}\right\rfloor }\right){\bmod {7}}+{\rm {{Tuesday}={\rm {Monday}}}}

작동 이유

최후의 날 규칙

종말일의 앵커 데이 계산은 기준 연도의 지정된 날짜와 현재 연도의 동일한 날짜 사이의 일 수를 효과적으로 계산한 다음 나머지 모듈로 7을 취한다. 두 날짜 모두 윤일(있는 경우) 이후에 오면 $365y$ + $y / 4$ (반올림)만 차이가 난다. 그러나 365는 52 × 7 + 1이다. 그래서 나머지를 취하면 우리는 단지

\left(y+\left\lfloor {y}{4}\right\bmd {7}).

이것은 $y$ 의 큰 값을 4와 7 둘 다로 나누는 것이 편하다면 더 간단한 공식을 제공한다. 예를 들어, 우리는 계산을 할 수 있다.

\left\lpage {\frac {66}{4}\right\bloor \오른쪽){\bmod {7}=(66+16){7}=82{\bmod {7}}}}{\bmod {7}=5

위의 예와 같은 대답을 제공한다.

12가 들어오는 것은 ( $y + yy / 4 ⌋)모드 7$ 의 패턴이 거의 12년마다 반복되는 것이다. 12년 후에 우리는 $(12$ + $12 / 4) mod$ 7 = $15 mod$ 7 = $1$ 을 얻는다. $y$ $mod 12$ 로 y를 대체하면, 우리는 이 여분의 날을 버리는 것이다. 그러나 $yy / 12$ ⌋을 다시 추가하면 이 오류를 보상하여 최종 공식을 제공한다.

"이상한 + 11" 방법

앵커 일수를 계산하는 Odd+11 방법을 보여주는 간단한 흐름도

올해의 앵커 데이를 찾는 더 간단한 방법은 체임벌린 퐁과 마이클 K에 의해 2010년에 발견되었다. 월터스는 제7차 산업 및 응용 수학에 관한 국제회의(2011년)에 제출된 논문에서 이렇게 기술했다.^[9] "이상한 + 11" 방법으로 불리는 이 방법은 컴퓨팅에 해당한다^[9].

\left(y+\left\lfloor {\frac {y}{4}}\right\rfloor \right){\bmod {7}}

+

\left(y+\left\lfloor {\frac {y}{4}}\right\rfloor \right){\bmod {7}}

y

\left(y+\left\lfloor {\frac {y}{4}}\right\rfloor \right){\bmod {7}}

\left(y+\left\lfloor {\frac {y}{4}}\right\rfloor \right){\bmod {7}}

)

\left(y+\left\lfloor {\frac {y}{4}}\right\rfloor \right){\bmod {7}}

7

{\

.

4(혹은 12)로 나누어야 할 필요가 없고, '이상 + 11' 규칙을 반복적으로 사용했기 때문에 절차가 기억하기 쉽기 때문에 정신적인 계산에 잘 맞는다. 게다가, 11까지 추가하면 베이스-10 산술에서 정신적으로 수행하기가 매우 쉽다.

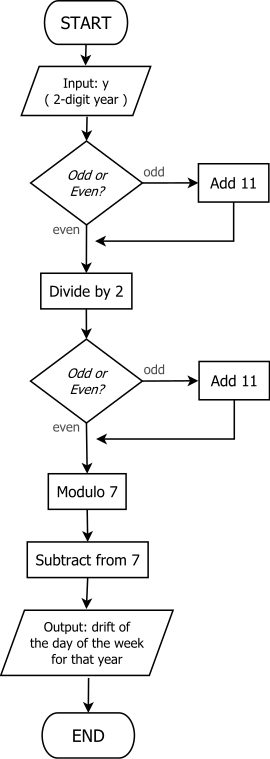
앵커 데이를 얻기 위해 이 절차를 연장하면, 흔히 다음과 같이 6단계로 총 주행 $T$ 를 축적하는 것으로 설명된다.

$T$ 를 올해의 마지막 두 자리수로 하자.
$T$ 가 홀수일 경우 11을 추가한다.
$이제$ T = $T / 2$ 로 하자.
$T$ 가 홀수일 경우 11을 추가한다.
$이제$ T = $7$ - $(T$ $mod$ 7)로 하자 $.$
세기의 앵커데이로부터 앞으로 $T일$ 을 세어 올해의 앵커데이를 얻는다.

예를 들어, 2005년에 이 방법을 적용하면 다음과 같이 요약된다.

$T = 5$
$T$ = $5$ + $11$ = $16$ ( $T$ 가 홀수이기 때문에 11을 추가)
$T = 16 / 2 = 8$
$T$ = $8$ ( $T$ 가 짝수이므로 아무 것도 안 함)
$T = 7 - (8모드 7) = 7 - 1 = 6$
2005년의 종말일 = 6 + 화요일 = 월요일

홀수+11 방법에 대한 명시적 공식은 다음과 같다.

7-\left[{\frac {y+11(y\,{\bmod {2}})}{2}}+11\left({\frac {y+11(y\,{\bmod {2}})}{2}}{\bmod {2}}\right)\right]{\bmod {7}}

.

이 표현은 위압적이고 복잡해 보이지만, 한 번만 계산하면 되는 공통적인 하위 표현 $y$ + $11(y mod$ 2 $)/ 2$ 때문에 실제로는 간단하다^[9].

언제든지 11을 추가해야 하며, 17개의 수율에서 동등한 결과를 뺀다. 17을 빼는 것이 11을 더하는 것보다 정신적으로 수행하기가 더 어려워 보일 수도 있지만, 특히 그 숫자가 7(예: 17, 27, 37, ..., 77, 87, 97)로 끝나는 두 자리 숫자일 때 17을 빼는 것이 더 쉬운 경우가 있다.

지배적인 편지와의 서신

최후의 날은 다음과 같이 그 해의 지배적인 글자와 관련이 있다.

둠스데이	도미니컬 문자
둠스데이	공통년도	윤년
일요일	C	DC
월요일	B	CB
화요일	A	BA
수요일	G	AG
목요일	F	GF
금요일	E	FE
토요일	D	ED

아래 표에서 도메인 문자(DL)를 찾아보십시오.

수백 년		D L	남은 연도 숫자				#
줄리안 (r ÷ 7)	그레고리안 (r ÷ 4)	D L	남은 연도 숫자				#
r5 19	16 20 r0	A	00 06 17 23	28 34 45 51	56 62 73 79	84 90	0
r4 18	15 19 r3	G	01 07 12 18	29 35 40 46	57 63 68 74	85 91 96	1
r3 17	해당 없음	F	02 13 19 24	30 41 47 52	58 69 75 80	86 97	2
r2 16	18 22 r2	E	03 08 14 25	31 36 42 53	59 64 70 81	87 92 98	3
r1 15	해당 없음	D	09 15 20 26	37 43 48 54	65 71 76 82	93 99	4
r0 14	17 21 r1	C	04 10 21 27	32 38 49 55	60 66 77 83	88 94	5
r6 13	해당 없음	B	05 11 16 22	33 39 44 50	61 67 72 78	89 95	6

2017년도의 경우, 영역별 글자는 A - 0 = A이다^{[needs update]}.

모든 Doomsday 개요

월	날짜	주 번호 *
1월(공통년)	3, 10, 17, 24, 31	1–5
1월(수평년)	4, 11, 18, 25	1–4
2월(공통년)	7, 14, 21, 28	6–9
2월(리프년)	1, 8, 15, 22, 29	5–9
3월	7, 14, 21, 28	10–13
4월	4, 11, 18, 25	14–17
5월	2, 9, 16, 23, 30	18–22
6월	6, 13, 20, 27	23–26
7월	4, 11, 18, 25	27–30
8월	1, 8, 15, 22, 29	31–35
9월	5, 12, 19, 26	36–39
10월	3, 10, 17, 24, 31	40–44
11월	7, 14, 21, 28	45–48
12월	5, 12, 19, 26	49–52

* 윤년에 n번째 종말일은 ISO 주 $n$ 에 있다. 보통 해에는 n번째 종말 다음날이 $n주이$ 다. 따라서 보통 해에는 종말일의 주 수 자체가 일요일인 경우, 즉 금요일부터 시작하는 보통 해의 주 수보다 한 배 적다.

1년 앵커 데이용 컴퓨터 공식

컴퓨터 사용을 위해, 1년의 앵커 데이에 대한 다음의 공식들이 편리하다.

그레고리력으로 다음 작업을 수행하십시오.

{\mbox{anchor day}}={\mbox{Tuesday}}+y+\left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor +\left\lfloor {\frac {y}{400}}\right\rfloor ={\mbox{Tuesday}}+5\times (y{\bmod {4}})+4\times (y{\bmod {1}}00)+6\times (y{\bmod {4}}00)

예를 들어 2009년의 종말일은 그레고리력으로 토요일이다(현재 승인된 달력).

{\mbox{Saturday (6)}{\bmod{7}={\mbox{Tuesday(2)}+2009+\lfloor{\frac{2009}{4}}}\right\bloor -\좌측\lfrac {2009}{100}\우측\floor +\lfloor {\frac {2009}{400}}\우측\loor }

또 다른 예로 1946년의 종말은 목요일이다.

{\mbox}Thursday (4)}}{\bmod {7}}={\mbox{Tuesday (2)}}+1946+\left\lfloor {\frac {1946}{4}}\right\rfloor -\left\lfloor {\frac {1946}{100}}\right\rfloor +\left\lfloor {\frac {1946}{400}}\right\rfloor

줄리안 달력의 경우:

{\mbox{anchor day}={\mbox{일요일}+y+\left\lpoor ={\frac{y}}}{\floor ={\mbox}}}}}+5회(y{\bmod {4}}}}}}})+3회(y{{{\bmod}}}}}}}}}}}}}}}}})

이 공식은 양력 달력과 양력 율리우스 달력에도 적용된다. 그들은 바닥 기능과 천문학 연도의 숫자를 기원전 몇 년 동안 사용한다.

비교는 줄리안 데이 번호 계산을 참조하십시오.

400년 주기 앵커 데이

율리우스 세기				-1600J -900J -200J 500J 1200J 1900J 2600J 3300J	-1500J -800J -100J 600J 1300J 2000J 2700J 3400J	-1400J -700J 0J 700J 1400J 2100J 2800J 3500J	-1300J -600J 100J 800J 1500J 2200J 2900J 3600J	-1200J -500J 200J 900J 1600J 2300J 3000J 3700J	-1100J -400J 300J 1000J 1700J 2400J 3100J 3800J	-1000J -300J 400J 1100J 1800J 2500J 3200J 3900J
그레고리안 수 세기 몇 해				-1600 -1200 -800 -400 0 400 800 1200 1600 2000 2400 2800 3200 3600		-1500 -1100 -700 -300 100 500 900 1300 1700 2100 2500 2900 3300 3700		-1400 -1000 -600 -200 200 600 1000 1400 1800 2200 2600 3000 3400 3800		-1300 -900 -500 -100 300 700 1100 1500 1900 2300 2700 3100 3500 3900
00	28	56	84	투에	몬	태양	앉았다	금요일	투	결혼하다
01	29	57	85	결혼하다	투에	몬	태양	앉았다	금요일	투
02	30	58	86	투	결혼하다	투에	몬	태양	앉았다	금요일
03	31	59	87	금요일	투	결혼하다	투에	몬	태양	앉았다
04	32	60	88	태양	앉았다	금요일	투	결혼하다	투에	몬
05	33	61	89	몬	태양	앉았다	금요일	투	결혼하다	투에
06	34	62	90	투에	몬	태양	앉았다	금요일	투	결혼하다
07	35	63	91	결혼하다	투에	몬	태양	앉았다	금요일	투
08	36	64	92	금요일	투	결혼하다	투에	몬	태양	앉았다
09	37	65	93	앉았다	금요일	투	결혼하다	투에	몬	태양
10	38	66	94	태양	앉았다	금요일	투	결혼하다	투에	몬
11	39	67	95	몬	태양	앉았다	금요일	투	결혼하다	투에
12	40	68	96	결혼하다	투에	몬	태양	앉았다	금요일	투
13	41	69	97	투	결혼하다	투에	몬	태양	앉았다	금요일
14	42	70	98	금요일	투	결혼하다	투에	몬	태양	앉았다
15	43	71	99	앉았다	금요일	투	결혼하다	투에	몬	태양
16	44	72		몬	태양	앉았다	금요일	투	결혼하다	투에
17	45	73		투에	몬	태양	앉았다	금요일	투	결혼하다
18	46	74		결혼하다	투에	몬	태양	앉았다	금요일	투
19	47	75		투	결혼하다	투에	몬	태양	앉았다	금요일
20	48	76		앉았다	금요일	투	결혼하다	투에	몬	태양
21	49	77		태양	앉았다	금요일	투	결혼하다	투에	몬
22	50	78		몬	태양	앉았다	금요일	투	결혼하다	투에
23	51	79		투에	몬	태양	앉았다	금요일	투	결혼하다
24	52	80		투	결혼하다	투에	몬	태양	앉았다	금요일
25	53	81		금요일	투	결혼하다	투에	몬	태양	앉았다
26	54	82		앉았다	금요일	투	결혼하다	투에	몬	태양
27	55	83		태양	앉았다	금요일	투	결혼하다	투에	몬

양력에는 146097일, 즉 정확히 20871주 7일이 있기 때문에 400년 동안 앵커 데이는 4세기마다 반복된다. 예를 들어, 1700–1799의 앵커 데이는 2100–2199의 앵커 데이(즉, 일요일)와 같다.

종말의 전체 400년 주기는 인접한 표에 제시되어 있다. 세기는 율리안을 위한 J로 표시하지 않는 한, 그레고리우스와 프릴렉틱 그레고리력을 위한 것이다. 그레고리우스 윤년이 강조되어 있다.

부정적인 해는 천문학적 연도 번호를 사용한다. 25년 BC는 -24로 76행의 -100J(촉각 줄리앙) 또는 -100(촉각 그레고리안) 열에 표시된다.

**평일 및 연도 유형별 400년 주기에서의 그레고리우스 운명의 빈도**
	일요일	월요일	화요일	수요일	목요일	금요일	토요일	합계
비리프년	43	43	43	43	44	43	44	303
윤년	13	15	13	15	13	14	14	97
합계	56	58	56	58	57	57	58	400

월요일을 최후의 날로 삼은 윤년은 일요일이 400년 연속 97일 중 하나라는 것을 의미한다. 따라서 일요일을 종일로 하는 총 연수는 71년으로 월요일을 종일로 하는 윤년 수를 뺀 것이다. 2000년 2월 29일에 걸쳐 월요일을 건너뛰고 윤일의 패턴이 윤일에 대칭이기 때문에 평일당(공통년 및 윤년 추가)의 빈도는 월요일을 기준으로 대칭적이다. 평일 당 윤년의 종말일 빈도는 2000년 화요일의 종말일에 대칭적이다.

특정 일자가 특정 평일에 있는 빈도는 위에서 쉽게 도출할 수 있다(1월 1일부터 2월 28일까지의 날짜는 전년도의 종말일과 관련).

예를 들어 2월 28일은 전년도의 종말 다음날이므로 화요일, 목요일, 일요일 등에는 각각 58회. 2월 29일은 윤년의 종말이라 월요일과 수요일 등에는 각각 15회씩이다.

28년 주기

줄리안 28년 주기에서의 종말의 빈도와 관련하여, 전자의 6, 17, 23년 후인 평일마다 1 윤년과 3년 후가 있다(따라서, 종말일 수에서 12년 후를 건너뛰기 때문에 균등하게 분포되지 않는다).^{[citation needed]} 동일한 주기가 특정 평일에 해당하는 3월 1일로부터 주어진 날짜에 적용된다.

특정 평일에 해당하는 2월 28일까지 주어진 날짜에 대해, 3개의 공통 연도는 윤년 후 5, 11, 22년이며, 따라서 5, 6, 6의 간격을 가진다. 따라서 주기는 동일하지만 윤년 이전이 아닌 5년 이후의 주기는 동일하다.

따라서 2월 29일을 제외한 모든 날짜에 대해 특정 평일에 속하는 공통 연도 사이의 간격은 6, 11, 11이다. 예를 들어 1906~2091년 범위의 연도를 월요일부터 시작하는 공통 연도 페이지의 하단을 참조하십시오.

특정 평일에 해당하는 2월 29일은 28년에 한 번 꼴로, 당연히 윤년이다.

율리우스력

그레고리력으로 현재 솔스트레스와 같은 천문학적 사건들이 정확하게 줄을 서고 있다. 1582년 줄리안 달력의 이러한 수정이 처음으로 시행되었다. 달력 표류를 수정하기 위해 10일을 건너뛰었으므로 종말이 10일(즉, 3일) 뒤로 이동했다. 10월 4일 목요일(줄리안, 종말일은 수요일), 10월 15일 금요일(그레고리안, 종말일은 일요일)이 뒤를 이었다. 이 표에는 줄리안 캘린더 연도가 포함되지만 알고리즘은 그레고리우스 및 프릴릭 그레고리력으로만 사용할 수 있다.

그레고리력으로 모든 국가에서 동시에 채택된 것은 아니므로 수세기 동안 지역마다 같은 날에 다른 날짜를 사용했다는 점에 유의하십시오.

전체 예시

예제 1(1985)

1985년 9월 18일의 요일을 알고 싶다고 가정합시다. 우리는 세기의 앵커 데이인 수요일부터 시작한다. 여기에 $a$ , $b$ , $c$ 를 위에 추가한다.

$a$ 는 $85 / 12$ 의 바닥으로, 7이다.
$b$ 는 $85모드12$ , 즉 $1$ 이다.
$c$ 는 $b / 4$ 의 바닥으로, 0이다.

이것은 + $b$ + $c$ = $8$ 을 산출한다. 수요일부터 8일을 세면 1985년의 종말일인 목요일에 도달한다. (숫자 사용: modulo 7 산술에서 8은 1과 일치한다. 세기의 앵커 데이는 수요일(지수 3)이고, 3 + 1 = 4이기 때문에 1985년의 종말은 목요일(지수 4)이었다. 우리는 이제 9월 18일을 가까운 종말일인 9월 5일과 비교한다. 우리는 18일이 종말일을 지나 13일이라는 것을 안다. 즉, 2주가 채 안 되는 날이다. 따라서 18일은 수요일(목요일 전날)이었다. (숫자 사용: modulo 7 산술에서 13은 6 또는 보다 간결하게 -1과 일치한다. 그러므로 우리는 1985년 9월 18일이 수요일이었음을 알기 위해 종말인 목요일에서 한 가지를 떼어낸다.)

예제 2(기타 세기)

1861년 4월 12일 섬터 요새에서 남북전쟁이 발발한 요일을 찾고 싶다고 가정하자. 세기의 앵커 데이는 목요일 이후 99일, 즉 금요일 ( $18$ + 1 $)\times 5 +$ + $18 / 44$ 으로 계산됨 $;$ 또는 세기의 앵커 데이를 나열한 위의 도표만 보면 된다. 61자리의 숫자가 6일이나 변위되어 있어서 최후의 날은 목요일이었다. 따라서 4월 4일은 목요일이었기 때문에 8일 후인 4월 12일은 금요일이었다.

참고 항목

서수일자
Computus – 부활절 날짜 계산을 위한 Gauss 알고리즘
젤러의 합치성 – 줄리안 또는 그레고리력으로 요일을 계산하는 알고리즘(1882).
멘탈 계산

참조

^ 존 호튼 콘웨이 "Tomorrow is the Day After Doomsday" (PDF). Eureka. October 1973. p. 28-32.
^ 리처드 가이, 존 호튼 콘웨이, 엘윈 베를캄프: "Winn Berlekamp: For Your Matheical Plays, Volume" 2: 게임스페셜" 795–797페이지, Academic Press, London, 1982, ISBN 0-12-091102-7페이지.
^ 루이스 캐롤, 1887년 3월 31일 네이처 "주말의 날을 찾아서". doi :10.1038/035517a0
^ 마틴 가드너, 손수건 속의 우주: 루이스 캐롤의 수학 레크리에이션, 게임, 퍼즐, 워드 플레이, 24-26페이지, 스프링거-베를라크, 1996.
^ "What Day is Doomsday". Mathematics Awareness Month. April 2014.
^ 앨퍼트, 마크 1999년 4월 사이언티픽 아메리칸 "Not Just Fun and Games". doi :10.1038/Scientific American0499-40
^ ^a ^b Torrence, Bruce; Torrence, Eve. "John H. Conway - Doomsday, part 1". YouTube. Mathematical Association of America. Archived from the original on 2021-12-21. Retrieved 14 April 2020.
^ Limeback, Rudy (3 January 2017). "Doomsday Algorithm". Retrieved 27 May 2017.
^ ^a ^b ^c 체임벌린 퐁, 마이클 K. Walters: "Conway의 Doomsday 알고리즘 가속을 위한 방법 (2부)", 제7차 산업 및 응용 수학 국제회의 (2011년)

외부 링크

한스-크리스티안 솔카의 평일 계산 백과사전, 2010
"모든 작업을 보여 주는" 종말 계산기
그레고리력으로 요일을 정신적으로 계산한 세계 기록
캘린더 날짜 찾기에 대한 국가 기록
세계 정신력 달력 날짜 랭킹(모든 경기 합산)
날짜를 지정하면 요일이 어떻게 되니?
Doomsday 알고리즘
요일 찾기
웨이백 머신에서 운명의 날 규칙을 설명하는 시(2006년 10월 18일 보관)

[1] 존 호튼 콘웨이 "Tomorrow is the Day After Doomsday" (PDF). Eureka. October 1973. p. 28-32.

[2] 리처드 가이, 존 호튼 콘웨이, 엘윈 베를캄프: "Winn Berlekamp: For Your Matheical Plays, Volume" 2: 게임스페셜" 795–797페이지, Academic Press, London, 1982, ISBN 0-12-091102-7페이지.

[3] 루이스 캐롤, 1887년 3월 31일 네이처 "주말의 날을 찾아서". doi :10.1038/035517a0

[4] 마틴 가드너, 손수건 속의 우주: 루이스 캐롤의 수학 레크리에이션, 게임, 퍼즐, 워드 플레이, 24-26페이지, 스프링거-베를라크, 1996.

[5] "What Day is Doomsday". Mathematics Awareness Month. April 2014.

[6] 앨퍼트, 마크 1999년 4월 사이언티픽 아메리칸 "Not Just Fun and Games". doi :10.1038/Scientific American0499-40

[Torrence-7] Torrence, Bruce; Torrence, Eve. "John H. Conway - Doomsday, part 1". YouTube. Mathematical Association of America. Archived from the original on 2021-12-21. Retrieved 14 April 2020.

[8] Limeback, Rudy (3 January 2017). "Doomsday Algorithm". Retrieved 27 May 2017.

[Odd11paper-9] 체임벌린 퐁, 마이클 K. Walters: "Conway의 Doomsday 알고리즘 가속을 위한 방법 (2부)", 제7차 산업 및 응용 수학 국제회의 (2011년)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Search

최후의 날 규칙

네임스페이스

더

목차

근현대 몇 년 동안의 앵커 데이

항상 운명의 날에 도착하는 기억에 남는 날짜

예

니모닉 평일 이름

1년 앵커 데이 찾기

작동 이유

"이상한 + 11" 방법

지배적인 편지와의 서신

모든 Doomsday 개요

1년 앵커 데이용 컴퓨터 공식

400년 주기 앵커 데이

28년 주기

율리우스력

전체 예시

예제 1(1985)

예제 2(기타 세기)

참고 항목

참조

외부 링크