적도 좌표계

구형 좌표를 사용한 적도 좌표계.기본 평면은 지구의 적도를 천구에 투영하여 천체를 형성한다. 천상의 적도일차 방향은 지구의 궤도를 천구에 투사하여 황도를 형성하고, 천적도에 황도의 상승 노드를 설정하여 춘분을 형성함으로써 설정된다.우측 상승은 천적도를 따라 동쪽에서 측정되며, 천적도에서 북쪽으로 양의 상승이 측정된다.(이러한 좌표 쌍 2개가 여기에 표시된다.)지구의 북쪽과 남쪽 지리적 극의 투영들은 각각 북쪽과 남쪽의 천극을 형성한다.

적도 좌표계는 천체의 위치를 명시하기 위해 널리 사용되는 천체 좌표계다.그것은 구면 또는 직사각형 좌표로 구현될 수 있으며, 둘 다 지구의 적도를 천구에 투영하는 것으로 구성된 기본 평면(천체 적도를 형성함), 춘분을 향한 일차 방향, 오른손잡이 관행에 의해 정의된다.^[1]^[2]

지구 중심에 있는 기원은 좌표가 지구중심적이라는 것을 의미하며, 즉 지구 중심에서 투명하게 보이는 것처럼 보인다.^[3]기본 평면과 일차 방향은 좌표계가 지구의 적도 및 극과 일직선으로 정렬되어 있지만 지구와 회전하지 않고 배경별에 대해 비교적 고정된 상태를 유지한다는 것을 의미한다.오른손잡이는 기본 평면을 중심으로 좌표가 북쪽에서 동쪽으로 증가하는 것을 의미한다.

1차 방향

기준 프레임의 방향에 대한 이 설명은 다소 단순하다. 방향은 상당히 고정되어 있지 않다.지구 축의 느린 움직임인 전열은 좌표계를 황색 극을 중심으로 서쪽으로 느리고 연속적인 회전을 일으켜 약 26,000년 만에 하나의 회로를 완성한다.여기에 겹쳐진 것은 에크리틱의 작은 움직임과 지구의 축인 견과류의 작은 진동이다.^[4]

정확한 일차 방향을 고정하기 위해 이러한 동작은 직위를 부여할 때 신기루라고 알려진 특정 날짜의 등분을 명기해야 한다.가장 일반적으로 사용되는 세 가지는 다음과 같다.

표준 epoch의 평균 분점(일반적으로 J2000.0, 그러나 B1950.0, B1900.0 등을 포함할 수 있음): 고정된 표준 방향이며, 다양한 날짜에 설정된 위치를 직접 비교할 수 있다.
날짜의 평균 분점: "날짜"(즉, "날짜"의 위치에 있는 황도)와 평균 적도(즉, 적도는 "날짜"의 위치로 전처리하여 회전하지만, 간질의 작은 주기적 진동으로부터 자유롭다)의 교차점이다.행성 궤도 계산에 일반적으로 사용된다.
날짜의 실제 분분: "날짜"의 황도와 참 적도의 교차점이다(즉, 평균 적도 + 견과).이것은 어떤 특정한 순간에 두 평면의 실제 교차점이며, 모든 움직임이 고려된다.

따라서 적도 좌표계의 위치는 일반적으로 J2000.0의 진분분과 적도, 평균분분과 적도 또는 이와 유사하게 지정된다.소량의 주기적 진동에 영향을 받지 않기 때문에 "만성 황색"은 없다는 점에 유의하십시오.^[5]

구형좌표

천문학에서 사용

항성의 구면 좌표는 거리 좌표 없이 종종 우측 상승과 표류로 표현된다.충분히 멀리 떨어져 있는 물체의 방향은 모든 관찰자에게 동일하며, 모든 관찰자에게 동일한 좌표로 이 방향을 지정하면 편리하다.이와는 대조적으로 수평 좌표계에서는 별의 위치가 지구 표면에서의 위치에 따라 관찰자마다 다르며, 지구의 자전에 따라 지속적으로 변화하고 있다.

적도의 산과 셋팅 원이 장착된 망원경은 물체를 찾기 위해 적도 좌표계를 사용한다.별 차트나 에페메리스와 함께 원을 설정하면 망원경이 천구의 알려진 물체를 쉽게 가리킬 수 있다.

탈위임

선언 기호 $Δ$ , (하위 케이스 "델타", 약칭 DEC)는 천적도에 수직인 물체의 각도 거리를 측정하고, 북쪽에는 양, 남쪽에는 음의 거리를 측정한다.예를 들어, 북극의 천체는 +90°의 열화를 가지고 있다.해체의 기원은 천적도인데, 이는 지구의 적도를 천구에 투영하는 것이다.분열은 지상 위도와 유사하다.^[6]^[7]^[8]

우측 상승

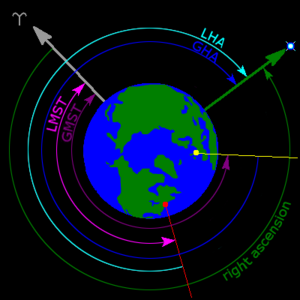
지구의 북극 위에서 볼 수 있듯이, 뉴욕 근처의 관측자를 위한 별의 국부적 시간 각도(LHA)이다.또한 별의 우측 상승과 그리니치 아워 각도(GHA), 국부 평균 사이드리얼 타임(LMST), 그리니치 평균 사이드리얼 타임(GMST)도 설명된다.기호 ʏ은 춘분 방향을 나타낸다.

우측 상승 기호 $α$ , (하위 사례 "알파", 약칭 RA)는 천적 적도를 따라 동쪽으로 물체의 각 거리를 춘분부터 물체를 통과하는 시원까지 측정한다.춘분점은 황도가 천적도와 교차하는 두 지점 중 하나이다.우측 상승은 보통 지구가 회전할 때 자오선을 가로지르는 물체의 통과 타이밍에 의해 우측 상승을 측정하는 방법의 결과로 도 대신 사이드리얼 시간, 분, 초 단위로 측정된다.있다360°/24^h = 오른쪽 상승 1시간 만에 15°, 오른쪽 상승 24^h° 전체 천체 적도를 중심으로.^[6]^[9]^[10]

함께 사용할 때, 우측 상승과 굴절은 보통 RA/Dec로 약칭된다.

시간 각도

우측 상승 대신, 시간 각도(약칭 HA 또는 LHA, 국부 시간 각도)는 관측자의 자오선으로부터 물체를 통과하는 시간 원까지의 천체 적도를 따라 서쪽으로 향하는 물체의 각도 거리를 측정한다.우측 상승과 달리 시간 각도는 항상 지구의 자전에 따라 증가하고 있다.시간 각도는 물체가 머리 위 자오선과 접촉한 순간인 상부 정점 이후 시간을 측정하는 수단으로 간주할 수 있다.

관찰자의 자오선에 있는 절정 별은 0시간 각도(0)를^h 가지고 있다고 한다.한 사이드리얼 시간(약 0.9973 태양 시간) 후, 지구의 자전은 별을 자오선 서쪽으로 운반할 것이며, 시간 각도는 1이^h 될 것이다.위상향 현상을 계산할 때, 우측 상승은 중간 단계로서 시간 각도로 변환될 수 있다.^[11]^[12]^[13]

직사각형 좌표

지구중심 적도 좌표

지구중심 적도 좌표기원은 지구의 중심이다.기본 평면은 지구의 적도면이다.1차 방향(

x축

)은 춘분이다.오른손잡이 규약은 기본 평면에서 동쪽으로 90°의

y축

을 지정하며,

z축

은 북극축이다.기준 프레임은 지구와 함께 회전하지 않고 오히려 지구가

z축

을 중심으로 회전한다.

적도 좌표의 직사각형 변형이 많다.모두 다음을 보유:

지구 중심에 있는 기원.
지구 적도 평면의 기본 평면.
춘분(x축)을 $향한$ 일차 방향, 즉 태양이 황반 주위를 연간 겉보기 회로로 북쪽 방향으로 천적 적도를 가로지르는 곳.
기본 평면에서 $동쪽$ 으로 90°의 y축과 북극 축을 $따라$ z축을 지정하는 오른손잡이 규약이다.

기준 프레임은 지구와 회전하지 않으며(지구 중심, 지구 고정 프레임과는 대조적으로), 항상 분류를 향해 있으며, 시간이 지남에 따라 전열과 견과류의 움직임으로 표류한다.

천문학에서:^[14]
- 태양의 위치는 종종 지리 중심 적도 직사각형 좌표 $X$ , $Y$ , $Z$ 와 네 번째 거리 좌표 $R$ $(=$ $\sqrt X 2$ + $Y 2 2$ + Z $)$ 에 천문단위 단위로 지정된다.
- 행성과 다른 태양계 신체의 위치는 종종 지리 적도 직사각형 좌표 $ξ$ , $η$ , $ζ$ 및 네 번째 거리 좌표 $Δ$ ( ( $ξ 2$ + $η 2$ + $η 2$ + ζ과 동일)에 천문단위 단위로 명시된다.
  이 직사각형 좌표는 다음에 의해 해당하는 구형 좌표와 관련된다. ${\begin{aligned}{\frac {X}{R}}={\frac {\xi }{\mathit {\Delta }}}&=\cos \delta \cos \alpha \\{\frac {Y}{R}}={\frac {\eta }{\mathit {\Delta }}}&=\cos \delta \sin \alpha \\{\frac {Z}{R}}={\frac {\zeta }{\mathit {\Delta }}}&=\sin \delta \end{aligned}}$
우주역학에서:^[15]
- 인공 지구 위성의 위치는 지구 적도 관성(GEI), 지구 중심 관성(ECI), 재래식 관성계(CIS)라고도 하는 지구 중심 적도 좌표로 지정되며, 이 모두 위의 천문 지구 중심 적도 직사각형 프레임과 동일한 정의에 해당한다.지리중심 적도 프레임에서 $x$ , $y$ , $z축$ 은 각각 $I$ , $J$ , $K$ 로 지정되거나 프레임의 기본은 단위 벡터 $ctors$ , $ĵ$ , $K$ 로 지정되는 경우가 많다 $.$
- 지구중심 천체 기준 프레임(GCRF)은 국제 천체 기준 프레임(ICRF)의 지구중심 등가물이다.그것의 1차 방향은 J2000.0의 등분이며, 전처리 및 견과와 함께 움직이지 않지만, 그 이외의 다른 방향은 위의 시스템과 동일하다.

천문 적도 좌표에^[16] 대한 표기법 요약

	구면			직사각형
	우측 상승	탈위임	거리	일반	특수 목적
지리학	$α$	$δ$	$Δ$	$ξ$ , $η$ , $ζ$	$X$ , Y, Z(Sun)
태양중심학				$x$ , $y$ , $z$

태양중심 적도 좌표

천문학에서는 또한 적도 좌표( $x$ , y, $z$ )의 태양중심 직사각형 변형이 있는데, 이 변형은 다음과 같다.

태양의 중심에 있는 기원.
지구 적도 평면의 기본 평면.
춘분을 향한 1차 방향( $x축$ )
기본 평면에서 $동쪽$ 으로 90°의 y축과 지구의 북극 축을 따라 $z축$ 을 지정하는 오른손잡이 규약이다.

이 프레임은 원점이 태양의 중심부로 제거되는 것을 제외하고 위의 $ξ$ , $η$ , $ζ$ 프레임에 해당하는 모든 방식으로 존재한다.그것은 일반적으로 행성 궤도 계산에 사용된다.3개의 천문 직사각형 좌표계는 다음과^[17] 같다.

#\displaystyle {\begin}\xi &=x+X\\eta &=y+Y\\\zeta &=z+Z\end{aigned}}

참고 항목

참조

^ Nautical Almanac Office, U.S. Naval Observatory; H.M. Nautical Almanac Office; Royal Greenwich Observatory (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London (reprint 1974). pp. 24, 26.
^ Vallado, David A. (2001). Fundamentals of Astrodynamics and Applications. Microcosm Press, El Segundo, CA. p. 157. ISBN 1-881883-12-4.
^ U.S. Naval Observatory Nautical Almanac Office; U.K. Hydrographic Office; H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. p. M2, "apparent place". ISBN 978-0-7077-4082-9.
^ 설명 보충판(1961), 페이지 20, 28
^ Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. p. 137. ISBN 0-943396-35-2.
^ ^a ^b Peter Duffett-Smith (1988). Practical Astronomy with Your Calculator, third edition. Cambridge University Press. pp. 28–29. ISBN 0-521-35699-7.
^ Meir H. Degani (1976). Astronomy Made Simple. Doubleday & Company, Inc. p. 216. ISBN 0-385-08854-X.
^ 천문연락 2010, p.M4
^ Moulton, Forest Ray (1918). An Introduction to Astronomy. p. 127.
^ 천문연락 2010, 페이지 M14
^ Peter Duffett-Smith (1988). Practical Astronomy with Your Calculator, third edition. Cambridge University Press. pp. 34–36. ISBN 0-521-35699-7.
^ 천문연락 2010, p.M8
^ 발라도(2001년), 페이지 154
^ 설명 보충판(1961), 페이지 24–26
^ Vallado(2001), 페이지 157, 158
^ 설명 보충판(1961년), 1G절
^ 설명 보충판(1961), 페이지 20, 27

외부 링크

[1] Nautical Almanac Office, U.S. Naval Observatory; H.M. Nautical Almanac Office; Royal Greenwich Observatory (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London (reprint 1974). pp. 24, 26.

[Vallado-2] Vallado, David A. (2001). Fundamentals of Astrodynamics and Applications. Microcosm Press, El Segundo, CA. p. 157. ISBN 1-881883-12-4.

[3] U.S. Naval Observatory Nautical Almanac Office; U.K. Hydrographic Office; H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. p. M2, "apparent place". ISBN 978-0-7077-4082-9.

[4] 설명 보충판(1961), 페이지 20, 28

[5] Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. p. 137. ISBN 0-943396-35-2.

[calculator28-6] Peter Duffett-Smith (1988). Practical Astronomy with Your Calculator, third edition. Cambridge University Press. pp. 28–29. ISBN 0-521-35699-7.

[simple-7] Meir H. Degani (1976). Astronomy Made Simple. Doubleday & Company, Inc. p. 216. ISBN 0-385-08854-X.

[8] 천문연락 2010, p.M4

[9] Moulton, Forest Ray (1918). An Introduction to Astronomy. p. 127.

[10] 천문연락 2010, 페이지 M14

[11] Peter Duffett-Smith (1988). Practical Astronomy with Your Calculator, third edition. Cambridge University Press. pp. 34–36. ISBN 0-521-35699-7.

[12] 천문연락 2010, p.M8

[13] 발라도(2001년), 페이지 154

[14] 설명 보충판(1961), 페이지 24–26

[15] Vallado(2001), 페이지 157, 158

[16] 설명 보충판(1961년), 1G절

[17] 설명 보충판(1961), 페이지 20, 27

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

Search