원거리장 회절의 수학적 설명
광학 에서 프라운호퍼 회절 방정식 은 회절 패턴을 회절 물체로부터 먼 거리에서 볼 때, 그리고 영상 렌즈 의 초점면 에서 볼 때도 파장의 회절 모델을 하기 위해 사용된다.[1] [2]
이 방정식은 조셉 폰 프라운호퍼(Joseph von Fraunhofer)를 기리기 위해 명명되었다. 비록 그는 이론의 발전에 실제로 관여하지는 않았지만 말이다.[3]
이 글은 다양한 수학적 형태로 방정식을 제공하며, 특히 일반적으로 입사 단색 평면 파형에 대해 여러 가지 다른 형태의 확산 개구부에 대한 프라운호퍼 회절 패턴의 상세한 계산을 제공한다. 프라운호퍼 회절의 질적 논의는 다른 곳 에서 찾아볼 수 있다.
정의 빛의 광선이 장애물에 의해 부분적으로 차단되었을 때, 어떤 빛은 물체 주위에 흩어지며, 빛과 어두운 띠가 그림자 가장자리에 종종 보인다 – 이 효과는 회절이라고 알려져 있다.[4] Kirchhoff 회절 방정식 은 개구부에 의해 분해되는 파동을 설명하는 파동 방정식에서 파생된 표현을 제공한다; 이 방정식에 대한 분석적 해법은 대부분의 구성에 사용할 수 없다.[5]
프라운호퍼 회절 방정식은 먼 장 에서 회절파가 관측될 때, 그리고 또한 렌즈를 사용하여 회절된 빛을 집중시킬 때 적용할 수 있는 근사값이다. 많은 경우, 프라운호퍼 방정식에 간단한 분석 용액을 사용할 수 있다. 그 중 몇 가지는 다음과 같다.
데카르트 좌표 좌표계가 있는 조리개(또는 분산 객체) 평면 및 영상 평면을 보여주는 회절 기하학. If the aperture is in x'y' monochromatic wave, of wavelength λ, wavenumber k complex amplitude A (x ',y ')x,y,z l ,m direction cosines of the point x,y U (x ,y ) 프라운호퍼 회절 방정식에 의해 다음과 같이 변형된 파형이 주어진다.[6]
U ( x , y , z ) ∝ ∬ 조리개 A ( x ′ , y ′ ) e − i 2 π λ ( l x ′ + m y ′ ) d x ′ d y ′ {\displaystyle U(x,y,z)\propto \iint _{\text{Aperture}\,A(x',y')e^{-i{\frac {2\pi }{\lambda }}}}{\lx'+my')\,dy'} U ( x , y , z ) ∝ ∬ 조리개 A ( x ′ , y ′ ) e − i k ( l x ′ + m y ′ ) d x ′ d y ′ {\displaystyle U(x,y,z)\propto \iint _{\text{Aperture}\,A(x',y')^{-ik(lx'+my')}\,dx'\,dy'} 회절 패턴의 형태는 보는 방향에만 좌우되기 때문에 회절 패턴은 크기는 변하지만 보는 거리의 변화로는 형태가 아니라는 것을 이 방정식을 통해 알 수 있다.
프라운호퍼 회절 방정식은 다양한 수학적으로 동등한 형태로 표현될 수 있다. 예를 들면 다음과 같다.[7]
U ( x , y , z ) ∝ ∬ 조리개 A ( x ′ , y ′ ) e − i 2 π λ z ( x ′ x + y ′ y ) d x ′ d y ′ {\displaystyle U(x,y,z)\propto \iint _{\text{Aperture}\,A(x',y')e^{-i{\frac {2\pi }{\lambda z}}}}\,dy'} U ( x , y , z ) ∝ ∬ 조리개 A ( x ′ , y ′ ) e − i k ( x ′ x + y ′ y ) z d x ′ d y ′ {\displaystyle U(x,y,z)\propto \iint _{\text{Aperture}\,A(x',y')e^{-i{\frac {k(x'x+y') }{z}}\,dx'\,dy'} 상기 방정식의 적분은 주파수에서[8] 푸리에 변환임 을 알 수 있다.
f x = x / ( λ z ) = l / λ {\displaystyle f_{x}=x/(\data z)=l/\data } f y = y / ( λ z ) = m / λ {\displaystyle f_{y}=y/(\da z)=m/\da } 따라서 푸리에 변환 의 관점에서 방정식을 다음과 같이 쓸 수도 있다.
U ( x , y , z ) ∝ f ^ [ A ( x ′ , y ′ ) ] f x f y {\displaystyle U(x,y,z)\propto {\hat {f}[A(x',y')]_{f_{x}f_{y}}}}} 여기서 A 푸리에 변환 공식은 회절 문제를 해결하는 데 매우 유용할 수 있다.
또 다른 형태는:
U ( r ) ∝ ∫ 조리개 A ( r ′ ) e − i k ⋅ ( r ′ − r ) d r ′ = ∫ 조리개 a 0 ( r ′ ) e i ( k 0 − k ) ⋅ ( r ′ − r ) d r ′ {\displaystyle U(\mathbf {r} )\propto {\int _{\text{Aperture}}A(\mathbf {r'} )e^{-i\mathbf {k} \cdot (\mathbf {r'} -\mathbf {r} )}dr'}={\int _{\text{Aperture}}a_{0}(\mathbf {r'} )e^{i\mathbf {(k_{0}-k)} \cdot (\mathbf {r'} -\mathbf {r} )}dr'}} 여기서 r 과 r' 나타내며0 k 교란과 확산파 의 파장 벡터를 각각0 나타내고, a(r ' )는 개구부의 교란 크기 를 나타낸다.
극좌표에서 분산형 개구부가 원형 대칭성을 가질 경우 데카르트 좌표보다는 극성 을 사용하는 것이 유용하다.[9]
개구부의 한 점 ,,Ω 이 있다.
x ′ = ρ ′ cas ω ′ ; y ′ = ρ ′ 죄를 짓다 ω ′ \displaystyle ~x'=\rho '\cos \omega ';y'=\rho '\sin \omega '} 그리고
x = ρ cas ω ; y = ρ 죄를 짓다 ω \displaystyle ~x=\rho \coses \omega ;y=\rho \sin \omega } ρ' 에서의 복잡한 진폭은 A(ρ )가 부여하고, dx dy 영역은 ρ ′ dω′ dΩ
U ( ρ , ω , z ) ∝ ∫ 0 ∞ ∫ 0 2 π A ( ρ ′ ) e − i 2 π λ z ( ρ ρ ′ cas ω cas ω ′ + ρ ρ ′ 죄를 짓다 ω 죄를 짓다 ω ′ ) ρ ′ d ρ ′ d ω ′ ∝ ∫ 0 2 π ∫ 0 ∞ A ( ρ ′ ) e − i 2 π λ z ρ ρ ′ cas ( ω − ω ′ ) d ω ′ ρ ′ d ρ ′ {\displaystyle {\reasoned} U(\rho ,\omega ,z)&,\propto\int _{0}^{\infty}\int _ᆯ^ᆰA(\rho의)e^{-i{\frac{2\pi}{z\lambda}}(\rho\rho '\cos\omega\cos \omega '+\rho\rho '\sin\omega\sin \omega의)}\rho'd\rho 'd\omega '\\&,\propto\int _{0}^{2\pi}\int _ᆵ^ᆶA(\rho의)e^{-i{\frac{2\pi}{z\lambda}}\rho '\cos(\omega -\omega의)\rho}'\rho '\,d \,d\omega.\rho '\e nd{정렬}}} Besel 함수 의 통합 표현 사용:[10]
J 0 ( p ) = 1 2 π ∫ 0 2 π e i p cas α d α {\displaystyle J_{0}(p)={\frac {1}{2\pi }}\int _{0}^{2\pi }e^{ip\cos \alpha }\,d\alpha }}}} 우리는 가지고 있다.
U ( ρ , z ) ∝ 2 π ∫ 0 ∞ A ( ρ ′ ) J 0 ( 2 π ρ ′ ρ λ z ) ρ ′ d ρ ′ {\displaystyle {\reasoned} U(\rho ,z)&\propto 2\pi \int _{0}^{\npty }A(\rho ') J_{0}\왼쪽({\frac {2\pi \rho '\rho \rho }{\lambda z}\right)\rho '\,d\rho '\ended}}}}}}} 등식이 원형 대칭이기 때문에 Ω 에 대한 통합이 2π 을 주는 경우, 즉 Ω 에 대한 의존성이 없다.
이 경우, 우리는 조리개 함수의 푸리에-베셀 또는 행클 변환 A (ρ 동등 (,,z ) 를 가진다.
예 여기에 보통 입사 단색 평면 파형에 의한 프라운호퍼 회절의 예가 제시되어 있다.
각 경우에 확산 물체는 z = 0 평면에 위치하며, 입사 평면 파형의 복잡한 진폭은 다음과 같이 주어진다.
A ( x ′ , y ′ ) = a e i 2 π c t / λ = a e i k c t {\displaystyle ~A(x',y')=ae^{i2\pi ct/\lambda }=ae^{ikct}} 어디에
a 규모 다.λ 은 파장이다,c t k 2π/λ 은 파형 번호 시간 위상 은 0이다.
시간 의존 인자는 일정하게 유지되기 때문에 계산 내내 생략되며, 강도를 계산 할 때 평균을 구한다. r 복잡한 결합
I ( r ) ∝ U ( r ) U ¯ ( r ) {\displaystyle I(\mathbf {r} )\propto U(\mathbf {r}){\overline {U}(\mathbf {r} )} 이러한 파생은 대부분의 표준 광학 서적에서 다양한 표기법을 사용하여 약간 다른 형태로 발견될 수 있다. 여기에서 모델링된 각 시스템에 대한 참조가 제공된다. 사용된 푸리에 변환은 여기 서 찾을 수 있다.
좁은 직사각형 슬릿 개구부는 너비 W
통합에 의한 솔루션 슬릿의 중심이 x 0 에 있다고 가정할 때 위의 첫 번째 방정식은 y [11]
U ( x , z ) = a ∫ − W / 2 W / 2 e − 2 π i x x ′ / ( λ z ) d x ′ = − a λ z 2 π i x e − 2 π i x x ′ / ( λ z ) − W / 2 W / 2 {\displaystyle {\begin{aligned}U(x,z)&=a\int _{-W/2}^{W/2}e^{{-2\pi ixx'}/(\lambda z)}\,dx'\\[4pt]&=-{\frac {a\lambda z}{2\pi ix}}\left e^{{-2\pi ixx'}/(\lambda z)}\right _{-W/2}^{W/2}\end{aligned}}} 오일러의 공식 을 사용하면 다음과 같이 단순화할 수 있다.
U ( x , z ) = a W 죄를 짓다 [ π W x λ z ] π W x λ z = a W 사악하게 하다 π W x λ z {\displaystyle {\begin}U(x,z)&=aW{\frac {\pi Wx}{\lambda z}\오른쪽]{\frac {\pi Wx}{\lambda z}\&=a W\operatorname {sinc} {\frac {\pi Wx}{\lambda z}\end{arged}}} 여기서 sinc (p ) sin(p )/p . sinc 함수는 때로 sin(sinp snp 로 정의되기도 하며 이는 다른 텍스트의 파생어를 볼 때 혼란을 야기할 수 있다.
이것은 또한 다음과 같이 쓰여질 수 있다.
U ( θ ) = a W 사악하게 하다 [ π W 죄를 짓다 θ λ ] {\displaystyle U(\theta )=aW\operatorname {sinc} \왼쪽[{\frac {\pi W\sin \theta }{\lambda }}\오른쪽]}} 여기서 θ sin θ 연결 하는 선 사이의 각이다.
푸리에 변환 솔루션 슬릿은 직장 기능으로 다음 과 같이 나타낼 수 있다.[12]
직장의 ( x W ) {\displaystyle ~\displayname {rect} \lefted\frac {x}{ W}\오른쪽)} 이 기능의 푸리에 변환 은 다음에 의해 주어진다.
f ^ ( 직장의 ( a x ) ) = 1 a ⋅ 사악하게 하다 ( ξ a ) {\displaystyle {\hat {f}(ax)}=\displaystyle {\frac {1}{{1}{}}}\cdot \cdot 이름 {sinc} \prec} \xi{a}\right)} 여기서 ξ 은 푸리에 변환 주파수이며 sinc 함수는 여기서 sin(πx πx
여기 푸리에 변환 빈도는 x /svz
U ( x , z ) ∝ W 죄를 짓다 π W x λ z π W x λ z ∝ W 사악하게 하다 π W x λ z ∝ W 사악하게 하다 π W 죄를 짓다 θ λ ∝ W 사악하게 하다 ( k W 죄를 짓다 θ / 2 ) {\displaystyle {\begin{aligned}U(x,z)&\propto W{\frac {\sin {\frac {\pi Wx}{\lambda z}}}{\frac {\pi Wx}{\lambda z}}}\\&\propto W\operatorname {sinc} {\frac {\pi Wx}{\lambda z}}\\&\propto W\operatorname {sinc} {\frac {\pi W\sin \theta }{\lambda }}\\&\propto W\operatorname {sinc} (kW\sin \theta /2)\end{aligned}}} sinc 함수는 일관성을 유지하기 위해 sin(x )/(x )로 정의된다는 점에 유의하십시오.
강도 강도 는 진폭의 제곱에 비례하므로 다음과[13]
I ( θ ) ∝ 사악하게 하다 2 [ π W 죄를 짓다 θ λ ] ∝ 사악하게 하다 2 [ k W 죄를 짓다 θ 2 ] {\displaystyle {\reasoned} I(\theta )&\propto \operatorname {sinc} ^{2}\왼쪽[{\frac {\pi W\sin \theta }{\lambda }}\오른쪽]\ \&\propto \operatorname {sinc} ^{2}\왼쪽[{\frac {kW\sin \theta }{2}}\right]\ended}}}}} 조리개 직사각형 조리개 직사각형 개구부에 의한 프라운호퍼 회절의 컴퓨터 시뮬레이션 파장 och 의 단색 평면 파장 에 의해 폭 W와 높이 H 의 직사각형 슬릿이 정상적으로 점등되는 경우(정상 각도에서 점등되는 슬릿) 다음과 같이 두 개의 독립적인 직교 치수에 걸쳐 적용된 이전 절의 그것과 유사한 분석을 사용하여 복잡한 진폭을 확인할 수 있다.[14] [15] [16]
U ( x ∝ sinc w x r sinc ( h y r c ( k 2 ( W x 2 R sinc k y 2 {\ displaystyle {\begin{igned} U(x,y)&\propto \operatorname {sinc} \좌({\frac {\pi Wx}{\lambda R}\우)\operatorname {sinc} \좌({\frac {\pi Hy}{\lambda R})\우) \\&\propto \operatorname {sinc} \좌측({\frac kWx}{2R}\우측)\ sinc} \좌측({\frac {kHy}{2R}\우측)\ended 강도는 에 의해 주어진다.
I ( x , y ) ∝ 사악하게 하다 2 ( π W x λ R ) 사악하게 하다 2 ( π H y λ R ) ∝ 사악하게 하다 2 ( k W x 2 R ) 사악하게 하다 2 ( k H y 2 R ) {\displaystyle {\reasoned} I(x,y)&\propto \operatorname {sinc} ^{2}\왼쪽({\pi Wx}{\lambda R}\오른쪽)\operatorname {sinc} ^{2}\pi Hy}{\lambda R}\오른쪽) \\&\propto \operatorname {sinc} ^{2}\왼쪽({\frac {kWx}{2R}\오른쪽)\operatorname {sinc} ^{2}\왼쪽({\frac {kHy}{2R}\오른쪽)\end{aigned}}}}}}}}}}}}}}}} 여기서 x축 y축 위 R 지점 x {\displaystyle P=(x,y)}
실제로 모든 슬릿은 크기가 유한하기 때문 폭 W 정의) 및 y 높이 H 정의) 축을 따라 양쪽 횡방향에 회절을 생성한다. 슬릿의 높이 H 가 폭 W 보다 훨씬 크면 수직(높이 또는 y축 x축 상대적으로 큰 H 에 의해 수직 가장자리 간격이 그렇게 적은 경우, 수직 프링의 관측은 너무 어려워서 관찰면이나 영상 평면에서 분산된 파동 강도 패턴을 관찰하는 사람은 좁은 높이로 수평 프링만 인식한다. 회절 그링과 같은 높이 길이의 슬릿 또는 슬릿 배열이 일반적으로 너비를 따라 치수에서만 분석되는 이유다. 조명 빔이 슬릿의 전체 높이를 비추지 않는 경우 수직 프링의 간격은 슬릿 높이를 따라 레이저 빔의 치수에 의해 결정된다. 아래 두 개의 슬릿 패턴을 자세히 살펴보면 주점 위와 아래에는 매우 미세한 수직 회절과 더 분명한 수평 프링들이 있음을 알 수 있다.
원형 조리개 구멍의 직경은 W 관측 평면의 복잡한 진폭은 다음에 의해 주어진다.
U ( ρ , z ) = 2 π a ∫ 0 W / 2 J 0 ( 2 π ρ ′ ρ λ z ) ρ ′ d ρ ′ {\displaystyle {\reasoned} U(\rho,z)&=2\pi a\int _{0}^{W/2}J_{0}\좌측({\frac {2\pi \rho \rho \}{\lambda z}\오른쪽)\rho '\d\rho '\end{liged}}}}}}}} 통합에 의한 솔루션 반복 관계[17]
d d x [ x n + 1 J n + 1 ( x ) ] = x n + 1 J n ( x ) {\displaystyle {\frac {d}{dx}\왼쪽[x^{n+1}J_{n+1}J_{n+1}(x)\right]=x^{n+1}J_{n}(x)} 주다
∫ 0 x x ′ J 0 ( x ′ ) d x ′ = x J 1 ( x ) {\displaystyle \int_{0}^{x}x' J_{0}(x')\,dx'=xJ_{1}(x)} 만약 우리가 대체한다면
x ′ = 2 π ρ λ z ρ ′ {\displaystyle x'={\frac {2\pi \rho }{\da z}\rho '}} 그리고 통합의 한계는 0이 되고 ρwW/zz 가 되면, 우리는
U ( ρ , z ) ∝ J 1 ( π W ρ / λ z ) π W ρ / λ z {\displaystyle U(\rho ,z)\propto {J_{1}(\pi W\rho /\lambda z)}{\pi W\rho /\lambda z}}{\pi W\rho /\lambda z}}}} puting θ , we get out.
U ( θ ) ∝ J 1 ( π W 죄를 짓다 θ / λ ) π W 죄를 짓다 θ / λ {\displaystyle U(\theta )\propto {\frac {J_{1}(\pi W\sin \theta /\lambda )}{\pi W\sin \theta /\lambda }}}} Fourier-Besel 변환을 사용한 솔루션 조리개 함수를 스텝 함수 로 쓸 수 있다.
Π ( W / 2 ) {\displaystyle ~\Pi(W/2)} 이 기능에 대한 푸리에-베셀 변환은 관계에 의해 주어진다.
F [ Π ( r / a ) ] = 2 π J 1 ( q a ) q {\displaystyle ~F[\Pi(r/a)]={\frac {2\pi J_{1}(qa)}{q}}}}} 여기서 q/2π 은 ρ/λz 및 a = W /2
그러므로 우리는 얻는다.
U ( ρ ) = 2 π J 1 ( π W ρ / λ z ) 2 π W ρ / λ z = 2 π J 1 ( π W 죄를 짓다 θ / λ ) W 죄를 짓다 θ / λ = 2 π J 1 ( k W 죄를 짓다 θ / 2 ) k W 죄를 짓다 θ / 2 {\displaystyle {\reasoned} U(\rho )&={\frac {2\pi J_{1}(\pi W\rho /\lambda z)}{2\pi W\rho /\lambda z}}\\&={\frac {2\pi J_{1}(\pi W\sin \theta /\lambda )}{W\sin \theta /\lambda }}\\&={\frac {2\pi J_{1}(kW\sin \theta /2)}{k W\sin \theta /2}}\end{aigned}} 강도 강도는 다음과 같다.[18]
I ( θ ) ∝ [ J 1 ( π W 죄를 짓다 θ / λ ) π W 죄를 짓다 θ / λ ) ] 2 ∝ [ J 1 ( k W 죄를 짓다 θ / 2 ) ( k W 죄를 짓다 θ / 2 ) ] 2 {\displaystyle {\reasoned} I(\theta )&\propto \left[{\frac {J_{1}(\pi W\sin \theta /\lambda )}{\pi W\sin \theta /\lambda )}}\right]^{2}\\&\propto \left[{\frac {J_{1}(kW\sin \theta /2)}{(kW\sin \theta /2)}}\right]^{2}\end{aligned}}} 회절 패턴의 형태 이것을 에어리 회절 패턴 이라고 한다.
확산된 패턴은 정규 축에 대해 대칭이다.
가우스 프로필이 있는 조리개 가우스 프로필이 있는 개구부를 통해 확산된 평면 파형의 강도 예를 들어, 전송이 가우스 변동을 갖는 사진 슬라이드와 같은 가우스 프로파일이 있는 개구부로서, 원점에서 r' 거리에 위치한 개구부의 한 지점에 진폭이 주어진다.
A ( ρ ′ ) = 생략하다 ( − [ ρ ′ σ ] 2 ) {\displaystyle A(\rho ')=\exp(-\좌측[{\frac[{\rho '}{\sigma }}}\오른쪽]^{2}\우측) }} 부여
U ( ρ , z ) = 2 π a ∫ 0 ∞ 생략하다 ( − [ ρ ′ σ ] 2 ) J 0 ( 2 π ρ ′ ρ / λ z ) ρ ′ d ρ ′ {\displaystyle U(\rho ,z)=2\pi a\int _{0}^{\inflit }\exp(왼쪽[{\frac {\rho '}}{\rho '}}}}{\sigma }^{2}\right)}}}} J_{0}(2\pi \rho '\rho /\lambda z)\rho '\d\rho '} Fourier-Besel 변환을 사용한 솔루션 푸리에-베셀 또는 행클 변환은 다음과 같이 정의된다.
F ν ( k ) = ∫ 0 ∞ f ( r ) J ν ( k r ) r d r {\displaystyle F_{\nu }(k)=\int _{0}^{\f(r)J_{\nu }\(kr)\,r\,dr} 여기서 J 는ν ν ≥ -1/2가 있는 첫 번째 종류의 주문 ν의 베셀 함수 다.
한클 의 변신은
F ν [ e ( a r ) 2 / 2 ] = e − k 2 / 2 a 2 a 2 {\displaystyle F_{\nu }[e^{{(ar)^{2}/2}]={\frac {e^{e^{-k^{2}}/2a^{2}}:{a^{2}}:}{a^{2}}:}}}{a^{2}}:} 부여
U ( ρ , z ) ∝ e − [ π ρ σ λ z ] 2 {\displaystyle {\reasoned} U(\rho,z)&\propto e^{-[{\frac {\pi \rho \sigma }{\lambda z}}}^{2}}\end{aigned}}}}}}}} 그리고
U ( θ ) ∝ e − [ π σ 죄를 짓다 θ λ ] 2 {\displaystyle U(\theta )\propto e^{-[{\frac {\pi \sigma \sigma \sin \theta }{\lambda }}^{2}}} 강도 강도는 다음과 같다.[19]
I ( θ ) ∝ e − [ 2 π σ 죄를 짓다 θ λ ] {\displaystyle I(\theta )\propto e^{-[{\frac {2\pi \sigma \sigma \sin \theta }{\lambda }}}}}}}}}}}}}}}}}}}}}} 이 함수는 오른쪽에 표시되며, 직사각형이나 원형 개구부에 의해 생성되는 회절 패턴과 달리 2차 고리가 없음을 알 수 있다. 이는 어포다이징(apodization )이라는 프로세스에서 사용될 수 있다. - 개구부는 가우스 함수로 전송이 달라 보조 링이 없는 회절 패턴을 제공하는 필터로 덮인다.[20] [21]
슬릿 슬릿 2개 두 개의 슬릿에서 분산된 빛이 겹칠 때 나타나는 패턴은 첫째, 영의 간섭 실험 을 통해 빛의 파동 이론을 확립하는 데 중요하고 둘째, 양자역학에서 이중 슬릿 실험 의 사고 실험으로서의 역할 때문에 물리학에 상당한 관심을 가지고 있다.
좁은 슬릿 우리 가 파장의 평면 파장에 의해 조명되는 두 개의 긴 슬릿을 가지고 있다고 가정하자.슬릿은 y축 z 0 평면에 있고 거리 S 슬릿의 폭은 파장에 비해 작다.
통합에 의한 솔루션 입사광은 슬릿에 의해 균일한 구면파로 분산된다. 두 슬릿에서 주어진 방향으로 이동하는 파도는 상이 다르다. 상·하부 슬릿에서 원점에 상대적인 파도의 위상은 (2π/λ)신(S/2 )신(神)과 -(2π/λ) 신(S/2) 신(神)으로 주어진다.
총 파형의 복잡한 진폭은 다음과 같이 주어진다.[22]
U ( θ ) = a e i π S 죄를 짓다 θ λ + a e − i π S 죄를 짓다 θ λ = a ( cas π S 죄를 짓다 θ λ + i 죄를 짓다 π S 죄를 짓다 θ λ ) + a ( cas π S 죄를 짓다 θ λ − i 죄를 짓다 π S 죄를 짓다 θ λ ) = 2 a cas π S 죄를 짓다 θ λ {\displaystyle {\reasoned} U(\theta)&, =ae^{\frac{i\pi S\sin \theta}{\lambda}}+ae^{-{\frac{i\pi S\sin \theta}{\lambda}}}\\&, =a(\cos{\frac{\pi S\sin \theta}{\lambda}}+i\sin{\frac{\pi S\sin \theta}{\lambda}})+a(\cos{\frac{\pi S\sin \theta}{\lambda}}-i\sin{\frac{\pi S\sin \theta}{\lambda}})\\&, =2a\cos{\frac{\pi S\sin \theta}{\lambda}}\end{alig.ned}}} 푸리에 변환을 사용한 솔루션 간극은 다음 함수로 나타낼 수 있다.[23]
a [ δ ( x − S / 2 ) + δ ( x + S / 2 ) ] {\displaystyle ~a[\delta {(x-S/2)}+\delta {(x+S/2)}} 여기서 Δ 는 델타 함수 다.
우리 는 가지고 있다.
f ^ [ δ ( x ) ] = 1 {\displaystyle {\hat{f}[\properties(x)]=1} 그리고
f ^ [ g ( x − a ) ] = e − 2 π i a f x f ^ [ g ( x ) ] {\displaystyle {\hat{f}[g(x-a)]=e^{-2\pi iaf_{x}{\hat {f}[g(x)]} 부여
U ( x , z ) = f ^ [ δ ( x − S / 2 ) + δ ( x + S / 2 ) ] = e − i π S x / 2 λ + e i π S x / 2 λ = 2 cas π S x 2 λ {\displaystyle {\begin}U(x,z)&={\hat {f}[\delta {(x-S/2)}+\delta {(x+S/2)}]\ \&=e^{-i\pi Sx/2\lambda }+e^{i\pi Sx/2\lambda }\&=2\cos {\frac {\pi Sx}{2\lambda }}}}\end{aigned}}}}}}}}}}}}}}}}} U ( θ ) = 2 cas π S 죄를 짓다 θ 2 λ {\displaystyle U(\theta )=2\cos {\frac {\pi S\sin \theta }{2\lambda }}} 이것은 통합에 의해 위에서 파생된 것과 같은 표현이다.
강도 이것은 다음과 같이 결합된 파장의 강도를 제공한다.[24]
I ( θ ) ∝ cas 2 [ π S 죄를 짓다 θ λ ] ∝ cas 2 [ k S 죄를 짓다 θ 2 ] {\displaystyle {\reasoned} I(\theta )&\propto \coses ^{2}\왼쪽[{\frac {\pi S\sin \theta }{\lambda }}}\ \&\propto \coses ^{2}{{2}}{\frac {kS\sin \theta }{2}}\오른쪽]}\end{arged}}}}}}}}}} 유한폭 슬릿 단일 및 이중 슬릿 회절 – 슬릿 분리 0.7mm, 슬릿 폭 0.1mm 슬릿의 폭, W
통합에 의한 솔루션 확산된 패턴은 다음과 같다.[25]
U ( θ ) = a [ e i π S 죄를 짓다 θ λ + e − i π S 죄를 짓다 θ λ ] ∫ − W / 2 W / 2 e − 2 π i x ′ 죄를 짓다 θ / ( λ ) d x ′ = 2 a cas π S 죄를 짓다 θ λ W 사악하게 하다 π W 죄를 짓다 θ λ {\displaystyle {\reasoned} U(\theta )&=a\left[e^{\frac {i\pi S\sin \theta }{\lambda }}+e^{-{\frac {i\pi S\sin \theta }{\lambda }}}\right]\int _{-W/2}^{W/2}e^{{-2\pi ix'\sin \theta }/(\lambda )}\,dx'\\&=2a\cos {\frac {\pi S\sin \theta }{\lambda }}W\operatorname {sinc} {\frac {\pi W\sin \theta }{\lambda }}\end{aligned}}} 푸리에 변환을 사용한 솔루션 조리개 기능은 다음과 같이 제공된다.[26]
a [ 직장의 ( x − S / 2 W ) + 직장의 ( x + S / 2 W ) ] {\style a\좌측[\operatorname {ret} \좌측({\frac {x-S/2}{W}\우측)+\operatorname {ret} \좌측({\frac {x+S/2}){{\frc}{\frac {x+S/}{}{}} W}\오른쪽)\오른쪽]} 이 기능의 푸리에 변환 은 다음에 의해 주어진다.
f ^ ( 직장의 ( a x ) ) = 1 a ⋅ 사악하게 하다 ( ξ a ) {\displaystyle {\hat {f}(ax)}=\displaystyle {\frac {1}{{1}{}}}\cdot \cdot 이름 {sinc} \prec} \xi{a}\right)} 여기서 ξ 은 푸리에 변환 주파수이며 sinc 함수는 여기서 sin(πx )/(πx )로 정의된다.
그리고
f ^ [ g ( x − a ) ] = e − 2 π i a f x f ^ [ g ( x ) ] {\displaystyle {\hat{f}[g(x-a)]=e^{-2\pi iaf_{x}{\hat {f}[g(x)]} 우리는 가지고 있다.
U ( x , z ) = f ^ [ a [ 직장의 ( x − S / 2 W ) + 직장의 ( x + S / 2 W ) ] ] = 2 W [ e − i π S x / λ z + e i π S x / λ z ] 죄를 짓다 π W x λ z π W x λ z = 2 a cas π S x λ z W 사악하게 하다 π W x λ z {\displaystyle {\begin}U(x,z)&={\hat {f}\좌측[\operatorname {ret} \좌측({\frac {x-S/2}{W}\우측)+\operatorname {ret} \좌측({\frac {x+S/2}){{{{{{}}}}} W}\오른쪽)\오른쪽]\오른쪽]\ \&=2W\left[e^{-i\pi Sx/\lambda z}+e^{i\pi Sx/\lambda z}\right]{\frac {\sin {\frac {\pi Wx}{\lambda z}}}{\frac {\pi Wx}{\lambda z}}}\\&=2a\cos {\frac {\pi Sx}{\lambda z}} W\operatorname {sinc} {\frac {\pi Wx}{\lambda z}\end{arged}}} 또는
U ( θ ) = 2 a cas π S 죄를 짓다 θ λ W 사악하게 하다 π W 죄를 짓다 θ λ {\displaystyle U(\theta )=2a\cos {\frac {\pi S\sin \din }{\lambda }W\operatorname {\pinc} {\frac {\pi W\sin }{\lambda }}}}}}}}}}}}}}} 이것은 통합에 의해 파생된 것과 같은 표현이다.
강도 강도는 다음과 같다.[27]
I ( θ ) ∝ cas 2 [ π S 죄를 짓다 θ λ ] 사악하게 하다 2 [ π W 죄를 짓다 θ λ ] ∝ cas 2 [ k S 죄를 짓다 θ 2 ] 사악하게 하다 2 [ k W 죄를 짓다 θ 2 ] {\displaystyle {\reasoned} I(\theta )&\propto \coses ^{2}\왼쪽[{\frac {\pi S\sin }}{\lambda }\right]\operatorname {sinc} ^{2}\frac {\pi W\sin }}{\lambda }\rig] \&\propto \coses ^{2}\왼쪽[{\frac {kS\sin }{2}}\오른쪽]\operatorname {sinc} ^{2}\왼쪽[{\frac {kW\sin }{{2}}\오른쪽]\ed}}}}}}}}}} 강도 패턴의 형태는 개별 슬릿 회절 패턴의 산물이며, 최소 폭의 슬릿으로 얻을 수 있는 간섭 패턴임을 알 수 있다. 이것은 레이저 빔에 의한 단일 슬릿 회절과 두 개의 동일한 슬릿에 의해 주어진 회절/간섭 패턴을 보여주는 오른쪽의 이미지에 설명되어 있다.
그라탕스 Born과 Wolf에서 그래팅은 "사건 파형에 진폭 또는 위상의 주기적 변동을 부과하는 모든 배열"로 정의된다.[28]
좁은 슬릿그링 단순 격자는 S
통합에 의한 솔루션 θ각 에서 확산파의 복잡한 진폭은 다음과 같이 주어진다.[29]
U ( θ ) = a ∑ n = 1 N e − i 2 π n S 죄를 짓다 θ λ = 1 − e − i 2 π N S 죄를 짓다 θ / λ 1 − e − i 2 π S 죄를 짓다 θ / λ {\displaystyle {\reasoned} U(\theta )&=a\sum _{n=1}^{N}e^{\frac {-i2\pi nS\sin \theta }{\lambda }}\\&={\frac {1-e^{-i2\pi NS\sin \theta /\lambda }}{1-e^{-i2\pi S\sin \theta /\lambda }}}\end{aligned}}}
이것이 기하 급수적인 시리즈 의 합이기 때문에.
푸리에 변환을 사용한 솔루션 간극은 다음에 의해 주어진다.
∑ n = 0 N δ ( x − n S ) {\displaystyle \sum _{n=0}^{N}\delta (x-nS)} 이 함수의 푸리에 변환은 다음과 같다.[30]
f ^ [ ∑ n = 0 N δ ( x − n S ) ] = ∑ n = 0 N e − i f x n S = 1 − e − i 2 π N S 죄를 짓다 θ / λ 1 − e − i 2 π S 죄를 짓다 θ / λ {\displaystyle {\begin{aigned}{\hat {f}\왼쪽[\sum _{n=0}^{n}^{n}\delta (x-nS)\right]&=\sum _{n=0}^{n}^{n}}} N}e^{-if_{x}nS}\\&={\frac {1-e^{-i2\pi NS\sin \theta /\lambda }}}{1-e^{-e2\pi S\sin \theta /\}\lambda }}}}}}}}}}}}}}}}}}}? 강도 20 및 50개의 좁은 슬릿그레이트 회절 패턴의 주 최대값 상세 강도는 다음과 같다.[31]
I ( θ ) ∝ 1 − cas ( 2 π N S 죄를 짓다 θ / λ ) 1 − cas ( 2 π S 죄를 짓다 θ / λ ) ∝ 죄를 짓다 2 ( π N S 죄를 짓다 θ / λ ) 죄를 짓다 2 ( π S 죄를 짓다 θ / λ ) {\displaystyle {\reasoned} I(\theta )&\propto {\frac {1-\cos(2\pi NS\sin \theta /\lambda )}{1-\cos(2\pi S\sin \theta /\lambda )}}\\&\propto {\frac {\sin ^{2}(\pi NS\sin \theta /\lambda )}{\sin ^{2}(\pi S\sin \theta /\lambda )}}\end{aligned}}}
이 함수는 맥시마와 미니마 시리즈를 가지고 있다. 주기적인 간격의 "maxima"와 주기적인 maxima 사이에 훨씬 더 작은 maxima가 있다. 주 최대값은 다음과 같은 경우에 발생한다.
π S 죄를 짓다 n θ / λ = n π , n = 0 , ± 1 , ± 2 , … {\displaystyle \pi S\sin _{n}\theta /\lambda =n\pi ,n=0,\pm 1,\pm 2,\ldots }} 따라서 주요 확산 빔은 각도에서 발생한다.
죄를 짓다 θ n = n λ S , n = 0 , ± 1 ± 2 , … {\displaystyle \sin \theta _{n}={\frac {n\lambda }{S},n=0,\pm 1\pm 2,\ldots } 이것은 보통 입사광에 대한 격자 방정식 이다.
소중간 최대치의 수는 슬릿 수 N 모양
N
20슬릿과 50슬릿의 상세 구조는 두 번째 다이어그램에 설명되어 있다.
유한폭 슬릿그링 이제 그링에는 너비 W S 슬릿 이 있다.
통합을 사용한 솔루션 진폭은 다음과 같이 지정된다.[32]
U ( θ , ϕ ) ∝ a ∑ n = 1 N e − i 2 π n S 죄를 짓다 θ λ ∫ − W / 2 W / 2 e − 2 π i x x ′ / ( λ z ) d x ′ ∝ a 사악하게 하다 ( π W 죄를 짓다 θ λ ) 1 − e − i 2 π N S 죄를 짓다 θ / λ 1 − e − i 2 π S 죄를 짓다 θ / λ {\displaystyle {\reasoned} U(\theta ,\phi )&\propto a\sum _{n=1}^{N}e^{\frac {-i2\pi nS\sin \theta }{\lambda }}\int _{-W/2}^{W/2}e^{{-2\pi ixx'}/(\lambda z)}\,dx'\\&\propto a\operatorname {sinc} \left({\frac {\pi W\sin \theta }{\lambda }}\right){\frac {1-e^{-i2\pi NS\sin \theta /\lambda }}{1-e^{-i2\pi S\sin \theta /\lambda }}}\end{aligned}}} 푸리에 변환을 사용한 솔루션 조리개 함수는 다음과 같이 기록할 수 있다.[33]
∑ n = 1 N 직장의 [ x ′ − n S W ] {\displaystyle \sum _{n=1}^{N}\operatorname {ret} \left[{\frac {x'-nS}{W}}\right]} 우리가 f (x )(x ) 두 가지 기능을 가지고 있다면, 그리고 우리는 다음과 같은 콘볼루션 정리 를 사용한다.
h ( x ) = ( f ∗ g ) ( x ) = ∫ − ∞ ∞ f ( y ) g ( x − y ) d y , {\displaystyle h(x)=(f*g)(x)=\int _{-\infit }^{\f(y)g(x-y)\,dy,} 여기서 ∗은 convolution operation을 의미한다. 그러면 우리는 또한
h ^ ( ξ ) = f ^ ( ξ ) ⋅ g ^ ( ξ ) . {\displaystyle {\h}(\xi )={\hat {f}(\xi )\cdot {\hat {g}(\xi). } 조리개 기능을 다음과 같이 쓸 수 있다.
직장의 ( x ′ / W ) ∗ ∑ n = 0 N δ ( x ′ − n S ) {\displaystyle \operatorname {ret}(x'/W)*\sum _{n=0}^{N}\delta(x'-nS)} 진폭은 이 식의 푸리에 변환에 의해 다음과 같이 주어진다.
U ( x , z ) = f ^ [ 직장의 ( x ′ / W ) ] f ^ [ ∑ n = 0 N δ ( x ′ − n S ) ] = a 사악하게 하다 ( W 죄를 짓다 θ λ ) 1 − e − i 2 π N S 죄를 짓다 θ / λ 1 − e − i 2 π S 죄를 짓다 θ / λ {\displaystyle {\begin}U(x,z)&={\hat {f}[\operatorname {ret}(x'/W)]{\f}\f}\좌측[\sum _{n=0}^{N}}\delta(x'-nS)\right]\\\\\\\\\\\\\]\ \&=a\operatorname {sinc} \좌({\frac {W\sin \theta }{\lambda }}\{\lambda }\pi NS\sin \theta }}{1-e^{-e^{-e2\pi\sin \}}}}}}정렬했다. 강도 강도는 다음과 같다.[34]
I ( θ ) ∝ 사악하게 하다 2 ( W 죄를 짓다 θ λ ) 죄를 짓다 2 ( π N S 죄를 짓다 θ / λ ) 죄를 짓다 2 ( π S 죄를 짓다 θ / λ ) {\displaystyle {\reasoned} I(\theta )&\propto \operatorname {sinc} ^{2}\left({\frac {W\sin \theta }{\lambda }}\right){\frac {\sin ^{2}(\pi NS\sin \theta /\lambda )}{\sin ^{2}(\pi S\sin \theta /\lambda )}}\end{aligned}}} 이 도표는 슬릿의 폭이 슬릿 분리의 1/5인 20슬릿으로 그링에 대한 회절 패턴을 보여준다. 주 확산 피크의 크기는 개별 슬릿의 회절 패턴으로 변조된다.
기타마음 위의 푸리에 변환 방법은 구조의 푸리에 변환이 알려진 모든 주기적 구조에 대한 회절 형태를 찾는 데 사용할 수 있다. 굿맨은[35] 이것들은 홀로그래피 에 특히 관심이 많다.
확장 비정규 조명 방향(l 0 ,m 0 ,n 0 ). [36]
U ( x , y , z ) ∝ ∬ 조리개 A ( x ′ , y ′ ) e − i 2 π λ [ ( l − l 0 ) x ′ + ( m − m 0 ) y ′ ] d x ′ d y ′ ∝ ∬ 조리개 A ( x ′ , y ′ ) e − i k [ ( l − l 0 ) x ′ + ( m − m 0 ) y ′ ] d x ′ d y ′ {\displaystyle {\reasoned} U(x,y,z)&\propto \iint _{\text{Aperture}}\,A(x',y')e^{-i{\frac {2\pi }{\lambda }}[(l-l_{0})x'+(m-m_{0})y']}\,dx'\,dy'\\&\propto \iint _{\text{Aperture}}\,A(x',y')e^{-ik[(l-l_{0})x'+(m-m_{0})y']}\,dx'\,dy'\end{aligned}}} 위의 각 시스템을 모델링하는 데 사용되는 방정식은 x y
그래팅 방정식은 다음과[37]
죄를 짓다 θ n = n λ S + 죄를 짓다 θ 0 , n = 0 , ± 1 , ± 2 , … {\displaystyle \sin \theta _{n}={\frac {n\lambda }{S}+\sin \theta _{0},n=0,\pm 1,\pm 2,\ldots }} 비 단색 조명 위의 프라운호퍼 회절의 모든 예에서 조명의 파장을 증가시키는 효과는 회절 구조의 크기를 줄이는 것이며, 반대로 파장을 줄이면 패턴의 크기가 커진다. 만약 빛이 단색광이 아니라면, 즉 그것은 다른 파장의 범위로 구성되며, 각각의 파장은 이웃과 약간 다른 크기의 패턴으로 확산된다. 파장의 확산이 평균 파장보다 현저히 작을 경우 개별 패턴의 크기가 거의 달라지지 않고, 따라서 기본 회절은 여전히 약간 줄어든 대비로 나타날 것이다. 파장 확산이 늘어나면서 관찰할 수 있는 '프링(fring)'이 줄어든다.
참고 항목 참조 ^ Born & Wolf, 1999, 페이지 427. ^ 젠킨스 & 화이트, 1957, 페이지 288 ^ "Fraunhofer, Joseph von (1787-1826) -- from Eric Weisstein's World of Scientific Biography" .^ 천국 & 배수로번, 1996, 페이지 62 ^ Born & Wolf, 2002, p 425 ^ 립슨 외, 2011, eq(8.8) 페이지 231 ^ 헤흐트, 2002, eq(11.63), p 529 ^ 헤흐트, 2002, eq(11.67), p 540 ^ Born & Wolf, 2002, 섹션 8.5.2, eqs(6–8), 페이지 439 ^ 아브라모위츠 & 스테건, 1964년, 섹션 9.1.21, 페이지 360 ^ Born & Wolf, 1999, 섹션 8.5.1 페이지 436 ^ 헤흐트, 2002, p 540 ^ 헤흐트, 2002, eqs (10.17), p 453 ^ Hecht, Eugene (2017). "10.2.4 The Rectangular Aperture". Optics (5th ed.). Pearson. pp. 483–488. ISBN 978-1-292-09693-3 ^ 롱허스트, 1967, 페이지 217 ^ Goodman, eq(4.28), p 76 ^ Whittaker와 Watson, 예 2, p 360 ^ 헤흐트, 2002, eq(10.56), p 469 ^ 헤흐트, 2002, eq(11.2), p 521 ^ 천국 & 배수로번, 1991년, 페이지 68 ^ 헤흐트, 2002, 그림(11.33), 페이지 543 ^ Jenkins & White, 1957, eq (16c), 페이지 312 ^ 헤흐트, 2002년, eq(11.4328), p 5 ^ Lipson 등, 2011, eq(9.3), p 280 ^ 헤흐트, 2002, 섹션 10.2.2, 페이지 451 ^ 헤흐트, 2002, 페이지 541 ^ Jenkins and White, 1967, eq(16c), p 313 ^ Born & Wolf, 1999, 섹션 8.6.1, 페이지 446 ^ Jenkins & White, 1957, eq(17a), p ^ Lipson 등, 2011, eq(4.41), p 106 ^ Born & Wolf, 1999, eq(5a), 페이지 448 ^ Born & Wolf, 섹션 8.6.1, eq(5), 페이지 448 ^ 헤흐트, 배열 정리, 페이지 543 ^ Born & Wolf, 2002, 섹션 8.6, eq(10), 페이지 451 ^ Goodman, 2005, 섹션 4.4.3 및 4.4.4, 페이지 78 ^ Lipson 외, 2011, 섹션 8.2.2, p 232 ^ Born & Wolf, 1999, eq (8), p 449
참조 소스 아브라모위츠 밀튼 & 스테건 아이린 A,1964, 뉴욕 도버 출판사 Born M & Wolf E, Principles of Optics ISBN 978-0-521-64222-4 Goodman Joseph, 2005, 로버츠 & Co. 푸리에 광학 소개 ISBN 0-9747077-2-4 또는 온라인 Oscene OS and Duturburn W, 1991년, Insight in Optics, Longman and Sons, Chichesterster ISBN 978-0-471-92769-3 헤히트 유진, 광학, 2002, 애디슨 웨슬리, ISBN 0-321-18878-0 Jenkins FA & White HE, 1957, Funderstance of Optics, 제3판, McGraw Hill, 뉴욕 Lipson A, Lipson SG, Lipson H , 2011, 광물리학 , 4번째 에드, 캠브리지 대학 출판부, ISBN 978-0-521-49345-1 Longhurst RS, 1967, 기하학적 및 물리적 광학, 제2판, Longmans, London 휘태커와 왓슨, 1962년 캠브리지 대학 출판부의 모던 애널리틱스. 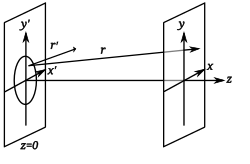






![U(x,y,z)\propto {\hat f}[A(x',y')]_{{f_{x}f_{y}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/827da252077afa33af507a455469cc5a49e918ea)









![{\displaystyle {\begin{aligned}U(x,z)&=a\int _{-W/2}^{W/2}e^{{-2\pi ixx'}/(\lambda z)}\,dx'\\[4pt]&=-{\frac {a\lambda z}{2\pi ix}}\left|e^{{-2\pi ixx'}/(\lambda z)}\right|_{-W/2}^{W/2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e72384a0879ebabd96de73062a27e81e06a33820)
![{\displaystyle {\begin{aligned}U(x,z)&=aW{\frac {\sin \left[{\frac {\pi Wx}{\lambda z}}\right]}{\frac {\pi Wx}{\lambda z}}}\\&=aW\operatorname {sinc} {\frac {\pi Wx}{\lambda z}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e8079719e70e2006ec4eee168c47fcc08c8c128)
![{\displaystyle U(\theta )=aW\operatorname {sinc} \left[{\frac {\pi W\sin \theta }{\lambda }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/559aa3cd80b0bd5e374a5123fbc761f1842a9809)



![{\displaystyle {\begin{aligned}I(\theta )&\propto \operatorname {sinc} ^{2}\left[{\frac {\pi W\sin \theta }{\lambda }}\right]\\&\propto \operatorname {sinc} ^{2}\left[{\frac {kW\sin \theta }{2}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23f8940e510be8fb31eae497643108e665466da3)






![{\frac {d}{dx}}\left[x^{{n+1}}J_{{n+1}}(x)\right]=x^{{n+1}}J_{n}(x)](https://wikimedia.org/api/rest_v1/media/math/render/svg/53af98c5968e3a20a51824a97facabd99cf02546)





![~F[\Pi (r/a)]={\frac {2\pi J_{1}(qa)}{q}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7db3e5fda430b68180a73c61d3b4e2873ea2f21b)

![{\begin{aligned}I(\theta )&\propto \left[{\frac {J_{1}(\pi W\sin \theta /\lambda )}{\pi W\sin \theta /\lambda )}}\right]^{2}\\&\propto \left[{\frac {J_{1}(kW\sin \theta /2)}{(kW\sin \theta /2)}}\right]^{2}\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3ceaff3087d33326acc12336bcbb55937f59dd2)

![A(\rho ')=\exp {\left(-\left[{\frac {\rho '}{\sigma }}\right]^{2}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f9227f546a228a2422dc0d79931e00110a6571a)
![U(\rho ,z)=2\pi a\int _{0}^{\infty }\exp {\left(-\left[{\frac {\rho '}{\sigma }}\right]^{2}\right)}J_{0}(2\pi \rho '\rho /\lambda z)\rho '\,d\rho '](https://wikimedia.org/api/rest_v1/media/math/render/svg/706846318f25ca95b0bc6e846848f65526fff1dd)

![F_{\nu }[e^{{(ar)^{2}/2}}]={\frac {e^{{-k^{2}/2a^{2}}}}{a^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ee69c2db51bfe8c70c8bed777ce3e7a8763a82d)
![{\begin{aligned}U(\rho ,z)&\propto e^{{-[{\frac {\pi \rho \sigma }{\lambda z}}]^{2}}}\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b85ac63a6a27e862967e10cdfac9d9394cc1d4e)
![U(\theta )\propto e^{{-[{\frac {\pi \sigma \sin \theta }{\lambda }}]^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9daaa66eb3194fa96d0d2b45924de33305597b9b)
![I(\theta )\propto e^{{-[{\frac {2\pi \sigma \sin \theta }{\lambda }}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b71303d412e20aa206d4aa5d245c7663d357a6c)



![~a[\delta {(x-S/2)}+\delta {(x+S/2)}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ec04a282225aefd5b61baa6adbf32420b014d10)
![{\hat {f}}[\delta (x)]=1](https://wikimedia.org/api/rest_v1/media/math/render/svg/d765dbe290d97d5ba5bf4e5056efe055dbfb1085)
![{\hat {f}}[g(x-a)]=e^{{-2\pi iaf_{x}}}{\hat {f}}[g(x)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d149808065d9b4830b9cf4159b645df22c7b1938)
![{\displaystyle {\begin{aligned}U(x,z)&={\hat {f}}[\delta {(x-S/2)}+\delta {(x+S/2)}]\\&=e^{-i\pi Sx/2\lambda }+e^{i\pi Sx/2\lambda }\\&=2\cos {\frac {\pi Sx}{2\lambda }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1b84838573ac106cc9dd18094ccaff7fd4f95ab)

![{\displaystyle {\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi S\sin \theta }{\lambda }}\right]\\&\propto \cos ^{2}{\left[{\frac {kS\sin \theta }{2}}\right]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0555e66edb580919787e84589ccad857b4a20298)

![{\displaystyle {\begin{aligned}U(\theta )&=a\left[e^{\frac {i\pi S\sin \theta }{\lambda }}+e^{-{\frac {i\pi S\sin \theta }{\lambda }}}\right]\int _{-W/2}^{W/2}e^{{-2\pi ix'\sin \theta }/(\lambda )}\,dx'\\&=2a\cos {\frac {\pi S\sin \theta }{\lambda }}W\operatorname {sinc} {\frac {\pi W\sin \theta }{\lambda }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c89b11bc6e39f37e085bdcd06c0f67b05bc6558d)
![{\displaystyle a\left[\operatorname {rect} \left({\frac {x-S/2}{W}}\right)+\operatorname {rect} \left({\frac {x+S/2}{W}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec0420b6d06178713fce93b12429ac4197a2f48f)
![{\displaystyle {\begin{aligned}U(x,z)&={\hat {f}}\left[a\left[\operatorname {rect} \left({\frac {x-S/2}{W}}\right)+\operatorname {rect} \left({\frac {x+S/2}{W}}\right)\right]\right]\\&=2W\left[e^{-i\pi Sx/\lambda z}+e^{i\pi Sx/\lambda z}\right]{\frac {\sin {\frac {\pi Wx}{\lambda z}}}{\frac {\pi Wx}{\lambda z}}}\\&=2a\cos {\frac {\pi Sx}{\lambda z}}W\operatorname {sinc} {\frac {\pi Wx}{\lambda z}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed93beb3da56f961ac6deee763d1df3d6d01833a)

![{\displaystyle {\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi S\sin \theta }{\lambda }}\right]\operatorname {sinc} ^{2}\left[{\frac {\pi W\sin \theta }{\lambda }}\right]\\&\propto \cos ^{2}\left[{\frac {kS\sin \theta }{2}}\right]\operatorname {sinc} ^{2}\left[{\frac {kW\sin \theta }{2}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/197ee093ddcc5286e0308f731d07125134c2c918)


![{\begin{aligned}{\hat {f}}\left[\sum _{{n=0}}^{{N}}\delta (x-nS)\right]&=\sum _{{n=0}}^{{N}}e^{{-if_{x}nS}}\\&={\frac {1-e^{{-i2\pi NS\sin \theta /\lambda }}}{1-e^{{-i2\pi S\sin \theta /\lambda }}}}\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb7e43ac1a73b794dd839934e03fcf0f92c6635d)







![{\displaystyle \sum _{n=1}^{N}\operatorname {rect} \left[{\frac {x'-nS}{W}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ae41623b808fac1fef16c4811779c8e529cde5d)



![{\displaystyle {\begin{aligned}U(x,z)&={\hat {f}}[\operatorname {rect} (x'/W)]{\hat {f}}\left[\sum _{n=0}^{N}\delta (x'-nS)\right]\\&=a\operatorname {sinc} \left({\frac {W\sin \theta }{\lambda }}\right){\frac {1-e^{-i2\pi NS\sin \theta /\lambda }}{1-e^{-i2\pi S\sin \theta /\lambda }}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/002f00cd39861a48319b8e2d6d8899e7b113d221)

![{\displaystyle {\begin{aligned}U(x,y,z)&\propto \iint _{\text{Aperture}}\,A(x',y')e^{-i{\frac {2\pi }{\lambda }}[(l-l_{0})x'+(m-m_{0})y']}\,dx'\,dy'\\&\propto \iint _{\text{Aperture}}\,A(x',y')e^{-ik[(l-l_{0})x'+(m-m_{0})y']}\,dx'\,dy'\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bff95fbf72e3482e2e46a78edf8f8cec7e51251)



