완벽한 해시함수

표시된 4개의 이름에 대한 완벽한 해시 함수

표시된 4개의 이름에 대한 최소 완벽한 해시 함수

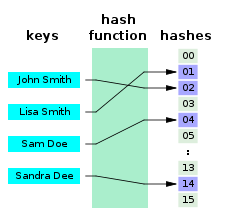
컴퓨터 과학에서 집합 $S$ 에 대한 완벽한 해시함수 $h$ 는 충돌 없이 $S$ 의 구별되는 요소들을 m $정수$ 에 매핑하는 해시함수다.수학적 용어로 말하면 주입함수다.

완벽한 해시 함수를 사용하여 최악의 액세스 시간이 일정한 룩업 테이블을 구현할 수 있다.완벽한 해시함수는, 어떤 해시함수처럼, 충돌 분해능을 구현할 필요가 없다는 이점으로 해시 테이블을 구현하는 데 사용될 수 있다.또한 키가 데이터가 아니고 쿼리된 키가 유효한 것으로 알려지면 키를 조회 테이블에 저장할 필요가 없어 공간을 절약할 수 있다.

완벽한 해시함수의 단점은 $S$ 가 완벽한 해시함수의 구축에 대해 알 필요가 있다는 점이다. $S$ 가 변경되면 비동적 완벽한 해시함수를 다시 구성할 필요가 있다.자주 변경되는 S의 경우 추가 공간의 비용으로 동적 완벽한 해시함수를 사용할 수 있다.^[1]완벽한 해시함수를 저장하기 위한 공간 요구사항은 $O (n$ )이다 $.$

완벽한 해시함수에 대한 중요한 성능 매개변수는 일정해야 하는 평가 시간, 시공 시간, 표현 크기 등이다.

적용

제한된 범위의 값을 가진 완벽한 해시함수는 함수의 출력에 의해 색인된 룩업 $테이블$ 에 S(또는 기타 관련 값)의 키를 배치함으로써 효율적인 룩업 연산을 위해 사용될 수 있다.그런 다음 $S$ 에 키가 있는지 테스트하거나, 테이블의 셀에서 키를 찾아 해당 키와 관련된 값을 검색할 수 있다.이런 조회는 매번 최악의 경우 일정한 시간이 걸린다.^[2]완벽한 해싱으로 관련 데이터를 읽거나 테이블에 대한 단일 액세스 권한으로 쓸 수 있다.^[3]

완벽한 해시함수의 성능

완벽한 해싱을 위한 중요한 성능 매개변수는 표현 크기, 평가 시간, 시공 시간 및 범위 ${\frac {m}{n}}$ ${\frac {m}{n}}$ ${\$ 이다 ${\frac {m}{n}}$ ^[4]평가 시간은 $O ($ 1) $만큼$ 빠를 수 있어 최적이다 $.$ ^[2]^[4] $S$ 의 각 요소는 고려되어야 하고, $S$ 는 $n개$ 의 요소를 포함하고 있기 때문에, 시공 시간은 $최소한$ O $(n$ )가 되어야 한다 $.$ 이 하한은 실제로 달성할 수 있다.^[4]

표현 크기에 대한 $하한$ 은 $m$ 과 n에 따라 다르다. $m =$ $(1+2) n$ 과 $h$ 를 완벽한 해시함수로 한다.하한에 대한 좋은 근사치는 $\log e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}$ $\log e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}$ e - $\log e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}$ $\log e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}$ 1 + $\log e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}$ ε $\log e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}$ {\ $displaystyle \log e-\varepsilon \log {\frac {1+\varepsilon }}{\varepsilon }}$ 원소당 비트 $\log e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}$ 수이다.최소 완벽한 해싱 $for$ = $0$ 의 경우, 하한은 원소당 $로그 e 1$ 1. $44비트$ 입니다.^[4]

건설

일정한 시간 내에, 그리고 작은 범위의 값을 가지고 평가될 수 있는 특정 $집합$ S에 대한 완벽한 해시함수는 S의 크기에 비례하는 다수의 연산에서 임의화된 알고리즘에 의해 찾을 수 있다.Fredman, Komloss & Szemerdi (1984)의 원래 구성은 2단계 체계를 사용하여 n $요소$ 의 $집합$ $S$ 를O( $n)$ 지수의 범위에 매핑한 다음 각 지수를 해시 값의 범위에 매핑한다.그들의 건설의 첫 번째 레벨은 큰 프라임 $p$ ( $S$ 가 그려진 우주의 크기보다 더 큰)와 매개변수 $k$ 를 선택하고, $S$ 의 각 원소 $x$ 를 지수에 매핑한다.

g(x)=(kx{\bmod {p}}){\bmod {n}.

$k$ 를 무작위로 선택하면 이 단계는 충돌이 일어날 가능성이 높지만, 동일한 지수 $i$ 에 동시에 매핑되는 원소 $n$ 의_i 수는 적을 가능성이 있다.두 번째 수준의 구성은 각 지수 $i$ 에 $O (n i 2)$ 정수의 이산형 범위를 할당한다.그것은 각 $지수$ i에 하나씩 있는 두 번째 선형 모듈식 함수를 사용하여 $S$ 의 각 $멤버$ $x$ 를 g $(x$ )와 연관된 범위에 매핑한다 $.$ ^[2]

프레드만, 코믈로스 & 스제메레디(1984)가 보여주듯이, $g (x)$ 의 n 다른 값에 대한 범위의 길이의 합이 $O (n$ )가 되도록 파라미터 $k$ 의 선택이 존재한다 $.$ 또한 $g (x)$ 의 각 값에 대해 해당 $S$ 의 부분 집합을 해당 값과 연관된 범위로 매핑하는 선형 모듈 함수가 존재한다. $k$ 와 $g (x$ )의 각 값에 대한 두 번째 수준 함수는 모두 다항식 시간에서 효과가 있는 값을 찾을 때까지 임의로 선택하여 찾을 수 있다 $.$ ^[2]

해시함수 자체는 $k$ , $p$ , 그리고 2차 레벨의 모든 선형 모듈 함수를 저장하기 위한 저장 $공간$ O $(n$ )를 요구한다.주어진 키 $x$ 의 해시값을 계산하는 $것$ 은 g $(x)$ 를 $계산$ 하고 g $(x$ )와 관련된 2차 수준의 함수를 찾아이 함수를 $x$ 에 적용함으로써 일정한 시간 내에 수행될 수 있다. 최상위 레벨에서 더 많은 수의 값을 갖는 이 2차 레벨 체계의 수정 버전을 사용하여 $S$ 를 sm으로 매핑하는 완벽한 해시함수를 구성할 수 있다. $전체$ 길이 범위 n + $o (n)$ ^[2]

완벽한 해시함수를 구성하기 위한 보다 최근의 방법은 Belazzougi, Botelho & Dietzfelbinger(2009)에 의해 "해시, 치환, 압축"이라고 기술되어 있다.여기서 1차 해시함수 $g$ 는 요소들을 $r$ 정수의 범위에 매핑하는데도 사용된다.요소 $x$ ∈ $S$ 는 버킷 $B$ 에_g(x) 저장된다.^[4]

그런 다음 크기 내림차순으로 φ부터 $시작$ 하여₁ 각 버킷의 요소는 독립된 완전 랜덤 해시함수( sequence, $φ 12,$ φ, $φ 3, ...)$ 의 시퀀스 해시함수에 의해 해시된다.해시함수가 버킷에 대한 충돌을 생성하지 않고 결과 값이 아직 다른 버킷의 다른 요소에 의해 점유되지 않은 경우, 해당 버킷에 대해 함수가 선택된다.그렇지 않으면 시퀀스의 다음 해시함수를 테스트한다.^[4]

완벽한 해시함수 $h (x)$ 를 평가하려면 버킷 인덱스 $g (x)$ 의 매핑 mapping만 시퀀스의 올바른 해시함수에 저장하면 되고, 그 결과 $h(x)$ = $φ$ 이_σ(g(x)) 된다.^[4]

마지막으로 표현 크기를 줄이기 위해 (ㄴ $(i) 0 \leq i < r$ 를 O(1)에서 여전히 평가가 가능한 형태로 압축한다 $.$ ^[4]

이 접근방식은 $시공$ 에 대해 n의 선형 시간과 일정한 평가 시간이 필요하다.표현 크기는 $O (n)$ 이며 달성된 범위에 따라 달라진다.예를 들어, $m = 1.23n$ Belazougi로 보텔호 & Dietzfelbinger(2009)는 주어진 1,000만 개의 항목 집합에 대해 3.03비트/키와 1.40비트/키 사이의 표현 크기를 달성했으며, 낮은 값은 더 높은 계산 시간이 필요하다.이 시나리오에서 하한 공간은 0.88비트/키다.^[4]

가성음

알고리즘 해시, 레이더, 찜질은(1) 갈라진 S양동이에 비:)g−1({나는})∩S,0 ≤ 나는 <, r(2)을 분류하는 순서로 크기의 rain 듣고(3)초기화 배열 T[0...m-1]0의(4)과 모든 i,(2)의 명령에 ∈[r]에 의하면 비에 심하게 흔들린다, 나는을(5)니 ← 1,2,...(6)반복한 기성용 ←{Φl()))비 ∈}(6)기성용)비와 Ki∩ 때까지{이다.jT[j]=1}= ∅(7) 모든 j에_i 대해 =(i):=성공 l (8)을 [ K에 대해 T[j]:= 1 (9) Transform (compression_i)_0≤i<r을 압축 형태로 하여  $O (1)$  접근을 유지하게 한다.

공간 하한

Fredman, Komloss & Szemerédi(1984)의 기능을 저장하기 위해 $O (n)$ 의 정보 단어를 사용하는 것은 거의 최적에 가깝다: 일정한 시간에 계산할 수 있는 완벽한 해시함수는 $S$ 의 크기에 비례하는 비트가 최소한 많이 필요하다.^[5]

최소 완벽한 해시 함수의 경우, 정보 이론적 공간 하한은 다음과 같다.

\log _{2}e\ 약 1.44

비트/^[4]키

완벽한 해시함수의 경우, $h$ 의 범위가 $n$ 으로m = ( $1+³)$ $n$ 으로 경계된다고 먼저 가정한다.Belazougi, Botelho & Dietzfelbinger(2009)가 제공한 공식과 $U$ = U = $u$ = 무한대로 향하는 우주 $U\supseteq S$ $U\supseteq S$ $U\supseteq S$ $U\supseteq S$ {\ $displaystyle$ U $\supseteq S}$ 의 경우, 공간 하한은 다음과 같다.

\log _{2}e-\varepsilon \log {\frac {1+\varepsilon }{\barepsilon }}

비트/키, $로그(n)$ 비트를 전체적으로 뺀 값.^[4]

확장

다이나믹 퍼펙트 해싱

자주 쿼리되는 대형 집합인 $S$ 가 있을 때 완벽한 해시함수를 사용하는 것이 가장 좋으며, 이는 거의 업데이트되지 않는다.이는 세트 $S$ 의 어떤 수정도 해시함수가 더 이상 수정된 세트에 완벽하지 않을 수 있기 때문이다.세트가 수정될 때마다 해시함수를 업데이트하는 솔루션은 동적 퍼펙트 해싱이라고 알려져 있지만,^[1] 이러한 방법은 구현하기가 비교적 복잡하다.

최소완벽 해시함수

최소완벽 해시함수는 $n키$ 를 $n개$ 의 연속 정수에 매핑하는 완벽한 해시함수(보통 $0$ 부터 $n$ - $1$ 까지 또는 $1$ 부터 $n$ 까지)이다.이것을 표현하는 좀 더 형식적인 $방법$ 은: $j$ 와 k를 어떤 $유한$ 집합 S의 요소가 되게 하라. $h (j)$ = $h (k)$ 가 $j$ = k(주사성)를 내포하고 $h$ 의 범위가 $a$ 인 정수 $a$ 가 존재하는 경우에만 $h$ 는 최소한의 완벽한 해시함수다 $.$ $a$ + $S$ - $1$ . 범용 최소 완벽 해시 체계에 적어도 1.44비트/키가 필요하다는 것이 입증되었다.^[4]현재 가장 잘 알려진 최소 완벽한 해싱 체계는 충분한 시간이 주어진다면 1.56비트/키를 사용하여 나타낼 수 있다.^[6]

완벽한 해싱

해시함수는 $S$ 의 대부분의 $k$ 요소가 범위의 동일한 값으로 매핑되는 경우 k-완벽하다."해시, 치환, 압축" 알고리즘을 사용해 $k-퍼펙트$ 해시함수를 최대 k-충돌까지 허용해 구성할 수 있다.이를 달성하는 데 필요한 변경사항은 최소 수준이며, 아래의 채택된 가성 부드에 밑줄이 그어져 있다.

(4) for all i ∈[r], in the order from (2), do (5)     for l ← 1,2,... (6)         repeat forming K_i ← { $Φ$ _l(x) x ∈ B_i} (6)         until  K_i = B_i and K_i∩{j T[j]=k}= ∅ (7)     let σ(i):= the successful l (8)     for all j ∈ K_i set T[j]←T[j]+1

주문보존

최소완벽 $해시함수$ F는 키가 $어떤 1$ $순서$ 로₂ a, a, $...,$ $a n$ , 그리고 어떤 $키$ 에_j $대해서$ 도_k j < $k$ 는 $F (a j)$ < F $(a k)$ ^[7]를 의미한다.이 경우 함수 값은 모든 키의 정렬된 순서에서 각 키의 위치에 불과하다.일정한 액세스 시간으로 주문 보존 최소의 완벽한 해시함수를 간단하게 구현하면 (일반적인) 완벽한 해시함수나 뻐꾸기 해싱을 사용하여 각 키의 위치 조회표를 저장하는 것이다.해시할 키 자체가 정렬된 배열로 저장되는 경우, 해시 값을 빠르게 계산하는 데 사용할 수 있는 데이터 구조에 키당 적은 수의 추가 비트를 저장할 수 있다.^[8]최소의 완벽한 해시함수를 주문 보존하려면 반드시 $Ω (n$ $log$ n $)$ 비트가 표시되어야 한다.^[9]

참조

^ ^a ^b Dietzfelbinger, Martin; Karlin, Anna; Mehlhorn, Kurt; Meyer auf der Heide, Friedhelm; Rohnert, Hans; Tarjan, Robert E. (1994), "Dynamic perfect hashing: upper and lower bounds", SIAM Journal on Computing, 23 (4): 738–761, doi:10.1137/S0097539791194094, MR 1283572.
^ ^a ^b ^c ^d ^e Fredman, Michael L.; Komlós, János; Szemerédi, Endre (1984), "Storing a Sparse Table with $O (1)$ Worst Case Access Time", Journal of the ACM, 31 (3): 538, doi:10.1145/828.1884, MR 0819156
^ Lu, Yi; Prabhakar, Balaji; Bonomi, Flavio (2006), "Perfect Hashing for Network Applications", 2006 IEEE International Symposium on Information Theory: 2774–2778, doi:10.1109/ISIT.2006.261567
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l Belazzougui, Djamal, Botelho, 파비아노 C;Dietzfelbinger, 마틴(2009년),"해시, 레이더, 그리고 compress"(PDF), Algorithms—.ESA2009년:17회 유럽 심포지엄, 덴마크 코펜하겐 9월 7-9,2009년, 저자(PDF), 강의 노트 컴퓨터 과학으로, 5757 vol., 베를린:스프링거,를 대신하여 서명함. 682–693, CiteSeerX 10.1.1.568.130, doi:10.1007/978-3-642-04128-0_61, MR2557794.
^ Fredman, Michael L.; Komlós, János (1984), "On the size of separating systems and families of perfect hash functions", SIAM Journal on Algebraic and Discrete Methods, 5 (1): 61–68, doi:10.1137/0605009, MR 0731857.
^ Esposito, Emmanuel; Mueller Graf, Thomas; Vigna, Sebastiano (2020), "RecSplit: Minimal Perfect Hashing via Recursive Splitting", 2020 Proceedings of the Symposium on Algorithm Engineering and Experiments (ALENEX), Proceedings, pp. 175–185, arXiv:1910.06416, doi:10.1137/1.9781611976007.14.
^ Jenkins, Bob (14 April 2009), "order-preserving minimal perfect hashing", in Black, Paul E. (ed.), Dictionary of Algorithms and Data Structures, U.S. National Institute of Standards and Technology, retrieved 2013-03-05
^ Belazzougui, Djamal; Boldi, Paolo; Pagh, Rasmus; Vigna, Sebastiano (November 2008), "Theory and practice of monotone minimal perfect hashing", Journal of Experimental Algorithmics, 16, Art. no. 3.2, 26pp, doi:10.1145/1963190.2025378.
^ Fox, Edward A.; Chen, Qi Fan; Daoud, Amjad M.; Heath, Lenwood S. (July 1991), "Order-preserving minimal perfect hash functions and information retrieval" (PDF), ACM Transactions on Information Systems, New York, NY, USA: ACM, 9 (3): 281–308, doi:10.1145/125187.125200.
^ Pagh, Rasmus; Rodler, Flemming Friche (2004), "Cuckoo hashing", Journal of Algorithms, 51 (2): 122–144, doi:10.1016/j.jalgor.2003.12.002, MR 2050140.

추가 읽기

리처드 J. 치첼리최소 퍼펙트 해시함수 단순화, ACM의 통신, Vol. 23, No. 1, 1980년 1월.
토마스 H. 코멘, 찰스 E. Leiserson, Ronald L. Rivest, Clifford Stein.알고리즘 소개, 제3판.MIT 프레스, 2009.ISBN 978-0262033848제11.5절: 완벽한 해싱, 페이지 267, 277–282.
파비아노 C.보텔호, 라스무스 파그, 니비오 지비아니."데이터 관리 애플리케이션을 위한 완벽한 해싱".
파비아노 C.보텔호와 니비오 지비아니."대형 키 세트를 위한 외부 완벽한 해싱"2007년 11월 포르투갈 리스본에서 열린 제16차 ACM 정보 및 지식 관리 회의(CIKM07),
자말 벨라조우기, 파올로 볼디, 라스무스 파그, 세바스티아노 비냐. "모노톤 최소 완벽 해싱: O(1) 액세스로 정렬된 테이블 검색"2009년 뉴욕, 이산 수학에 관한 제 20회 연례 ACM-SIAM 심포지엄의 진행에서.ACM Press.
더글러스 C.슈미트, GPERF: 완벽한 해시함수 생성기, C++ 보고서, SIGS, Vol. 10, 1998년 11월/12월.

외부 링크

gperf는 오픈 소스 C 및 C++ 완벽한 해시 생성기(매우 빠르지만 작은 세트에서만 작동)
밥 젠킨스의 미니멀 퍼펙트 해싱(bob 알고리즘)
cmph: C Minimal Perfect Hashing Library, 여러 (최소) 완벽한 해시를 위한 오픈 소스 구현(빅 세트용 작업)
Sux4J: Java에서 오픈 소스 모노톤 최소 완벽 해싱
MPHSharp: C#의 완벽한 해싱 방법
BBHASH: 헤더 전용 C++의 최소 완벽한 해시 함수
완벽::해시, C 코드를 만드는 Perl의 완벽한 해시 생성기.볼만한 "사전 예술" 코너가 있다.

[DynamicPerfectHashing-1] Dietzfelbinger, Martin; Karlin, Anna; Mehlhorn, Kurt; Meyer auf der Heide, Friedhelm; Rohnert, Hans; Tarjan, Robert E. (1994), "Dynamic perfect hashing: upper and lower bounds", SIAM Journal on Computing, 23 (4): 738–761, doi:10.1137/S0097539791194094, MR 1283572.

[inventor-2] Fredman, Michael L.; Komlós, János; Szemerédi, Endre (1984), "Storing a Sparse Table with $O (1)$ Worst Case Access Time", Journal of the ACM, 31 (3): 538, doi:10.1145/828.1884, MR 0819156

[3] Lu, Yi; Prabhakar, Balaji; Bonomi, Flavio (2006), "Perfect Hashing for Network Applications", 2006 IEEE International Symposium on Information Theory: 2774–2778, doi:10.1109/ISIT.2006.261567

[CHD-4] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l Belazzougui, Djamal, Botelho, 파비아노 C;Dietzfelbinger, 마틴(2009년),"해시, 레이더, 그리고 compress"(PDF), Algorithms—.ESA2009년:17회 유럽 심포지엄, 덴마크 코펜하겐 9월 7-9,2009년, 저자(PDF), 강의 노트 컴퓨터 과학으로, 5757 vol., 베를린:스프링거,를 대신하여 서명함. 682–693, CiteSeerX 10.1.1.568.130, doi:10.1007/978-3-642-04128-0_61, MR2557794.

[5] Fredman, Michael L.; Komlós, János (1984), "On the size of separating systems and families of perfect hash functions", SIAM Journal on Algebraic and Discrete Methods, 5 (1): 61–68, doi:10.1137/0605009, MR 0731857.

[RecSplit-6] Esposito, Emmanuel; Mueller Graf, Thomas; Vigna, Sebastiano (2020), "RecSplit: Minimal Perfect Hashing via Recursive Splitting", 2020 Proceedings of the Symposium on Algorithm Engineering and Experiments (ALENEX), Proceedings, pp. 175–185, arXiv:1910.06416, doi:10.1137/1.9781611976007.14.

[7] Jenkins, Bob (14 April 2009), "order-preserving minimal perfect hashing", in Black, Paul E. (ed.), Dictionary of Algorithms and Data Structures, U.S. National Institute of Standards and Technology, retrieved 2013-03-05

[8] Belazzougui, Djamal; Boldi, Paolo; Pagh, Rasmus; Vigna, Sebastiano (November 2008), "Theory and practice of monotone minimal perfect hashing", Journal of Experimental Algorithmics, 16, Art. no. 3.2, 26pp, doi:10.1145/1963190.2025378.

[9] Fox, Edward A.; Chen, Qi Fan; Daoud, Amjad M.; Heath, Lenwood S. (July 1991), "Order-preserving minimal perfect hash functions and information retrieval" (PDF), ACM Transactions on Information Systems, New York, NY, USA: ACM, 9 (3): 281–308, doi:10.1145/125187.125200.

[10] Pagh, Rasmus; Rodler, Flemming Friche (2004), "Cuckoo hashing", Journal of Algorithms, 51 (2): 122–144, doi:10.1016/j.jalgor.2003.12.002, MR 2050140.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Search