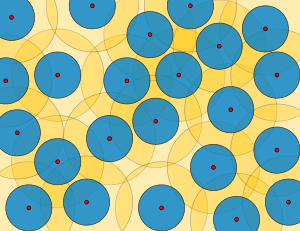
델론 세트

Delone set
적색 지점은 유클리드 평면에 대한 ε-넷의 일부를 형성하며, 여기서 ε은 큰 황색 원반의 반지름이다.반경의 절반인 파란색 원반은 분리되어 있고, 노란색 원반은 전체 평면을 커버하며, net-net 상의 두 가지 정의 요건을 충족한다.

미터법 공간의 수학적 이론에서 ε-nets, pack-패킹, cover-커버링, 균일하게 이산된 집합, 비교적 밀도 집합, 델론 집합(보리스 델론의 이름을 딴 이름)은 잘 간격을 두고 있는 점 집합의 여러 가지 정의로, 이러한 집합의 패킹 반경과 커버 반경이 얼마나 잘 간격을 두고 있는지 측정한다.이들 집합은 코딩 이론, 근사 알고리즘, 퀘이시크리스탈 이론에 응용이 있다.

정의들

(M,d)가 미터법 공간이고, X가 M의 부분집합인 경우, X의 패킹 반경은 X의 구별되는 부재 사이의 거리 최소값의 절반이다.패킹 반경이 r인 경우 X 지점 중심의 r반경의 오픈볼이 모두 분리되고, 반지름 2r의 X 지점 중 하나에 집중된 각 오픈볼은 나머지 X 지점으로부터 분리된다.X의 피복 반지름은 숫자 r의 최소값으로 M의 모든 지점이 X의 최소 1 포인트의 거리 r 내에 있도록 한다. 즉, X의 지점을 중심으로 한 해당 반지름의 닫힌 볼이 M의 모두를 결합으로 갖는 가장 작은 반지름이다.ε패킹은 패킹 반지름 //2의 집합 X(동일하게 최소 거리 ≥ ≥)이며, ε 커버링은 커버 반지름 ≤의 집합 X이며, ε 네트는 ε패킹과 ε 커버링의 집합이다.세트는 0이 아닌 패킹 반경을 가진 경우 균일하게 이산형이며, 커버 반경이 유한한 경우 비교적 밀도가 높다.델론 집합은 균일하게 이산형이며 비교적 밀도가 높은 집합이다. 따라서 모든 ε넷은 델론이지만 그 반대의 경우는 아니다.[1][2]

ε-net 구축

위의 정의 중 가장 제한적인 것으로서, ε-net은 적어도 ε-패킹, ε-커버링, 델론 세트만큼 구성하기 어렵다.그러나, M의 지점이 순서가 잘 되어 있을 때마다, 트랜스피니트 유도는 순서에서 이전 지점들의 집합까지의 거리의 최소치가 최소한 ε인 모든 점을 N에 포함시킴으로써 net-net N을 구성할 수 있음을 보여준다.경계 치수의 유클리드 공간에 있는 유한한 점 집합의 경우, 직경 ε의 셀 격자에 매핑하여 각 점을 일정한 시간 내에 시험할 수 있으며, 해시 테이블을 사용하여 이미 N의 점을 포함하고 있는 근처 셀을 시험할 수 있으므로, 이 경우 ε넷은 선형 시간 내에 구축할 수 있다.[3][4]

보다 일반적인 유한하거나 컴팩트한 메트릭스 공간의 경우, 가장 먼 첫 번째 트래버설 기반의 Teo Gonzalez의 대체 알고리즘을 사용하여 유한 net-넷을 구축할 수 있다.이 알고리즘은 네트 N이 비어있도록 초기화한 다음, 반복적으로 N에서 M의 가장 먼 지점을 N에 추가함으로써 임의로 동점을 끊고 M의 모든 지점이 N의 거리 ε 이내에 있을 때 정지한다.[5]경계 더블링 치수의 공간에서 곤잘레스의 알고리즘은 가장 먼 거리와 가장 가까운 거리 사이의 다항 비율을 갖는 점 집합에 대해 O(n log n) 시간으로 구현될 수 있으며 임의 점 집합에 대해 동일한 시간 경계로 근사치를 구할 수 있다.[6]

적용들

코딩 이론

주요 기사:해밍 결합 § 커버 반경 및 패킹 반경

오류 수정 코드 이론에서 블록 코드 C를 포함하는 메트릭 공간은 해밍 메트릭과 함께 크기 q의 알파벳(벡터라고 생각할 수 있음)을 넘겨받는 고정 길이의 문자열(n)으로 구성된다.이 공간은 에 의해 표시된다이 미터법 공간의 커버 반지름과 패킹 반경은 코드의 오류 수정 능력과 관련이 있다.

근사 알고리즘

Har-Peled & Raichel(2013)은 유클리드 공간의 점 집합에 정의된 특정 유형의 기하학적 최적화 문제에 대한 근사 알고리즘을 설계하기 위해 그들이 "넷과 가지치기"라고 부르는 알고리즘 패러다임을 설명한다.이 유형의 알고리즘은 다음 단계를 수행하여 작동한다.

  1. 점 집합에서 임의 점 p를 선택하고 가장 가까운 인접 q를 찾은 다음 ε을 p와 q 사이의 거리로 설정하십시오.
  2. ε이 최적 솔루션 값보다 크거나 작은지 테스트(해결 중인 특정 최적화 문제에 특정한 기법을 사용)
    • 크기가 클 경우 가장 가까운 이웃이 ε보다 먼 점을 입력에서 제거한다.
    • 크기가 작으면 ε-net N을 구성하고 입력에서 N에 없는 점을 제거한다.

두 경우 모두 남은 점의 예상 개수가 일정 요인만큼 감소하므로 시간은 시험 단계에 의해 지배된다.그들이 보여주듯이, 이 패러다임은 k-center 클러스터링에 대한 빠른 근사 알고리즘을 구축하기 위해 사용될 수 있으며, 중앙분리대의 거리를 가진 점 쌍과 관련된 여러 문제를 찾을 수 있다.

그물-트리라고 불리는 그물의 계층적 시스템은 잘 분리된 쌍 분해, 기하학적 스패너 및 근접한 가까운 이웃을 구성하기 위해 경계 이중화 차원의 공간에 사용될 수 있다.[6][7]

결정학

유클리드 공간의 점의 경우, 세트 X는 상대적으로 밀도가 높고 차이 세트 X - X가 균일하게 이산된 경우 마이어 집합이다.마찬가지로 X와 X - X가 모두 델론일 경우 X는 마이어 집합이다.마이어 세트는 이브 마이어의 이름을 따서 명명되었는데, 그는 퀘이시크리스탈의 수학적 모델로서 (조화학적 분석에 기초한 다르지만 동등한 정의로) 소개했다.이들 세트에는 래티스 포인트 세트, 펜로즈 틸링, 유한 세트 세트의 민코스키 합계가 포함된다.[8]

대칭 델론의 보로노이 세포는 플레시오헤드라라 불리는 공간을 채우는 다면체를 형성한다.[9]

참고 항목

참조

  1. ^ Clarkson, Kenneth L. (2006), "Building triangulations using ε-nets", STOC'06: Proceedings of the 38th Annual ACM Symposium on Theory of Computing, New York: ACM, pp. 326–335, doi:10.1145/1132516.1132564, ISBN 1595931341, MR 2277158.
  2. ^ 일부 소스는 여기서 "복제 커버링"이라고 하는 것에 대해 "복제 네트"를 사용한다. 예: 참조.
  3. ^ Har-Peled, S. (2004), "Clustering motion", Discrete and Computational Geometry, 31 (4): 545–565, doi:10.1007/s00454-004-2822-7, MR 2053498.
  4. ^ Har-Peled, S.; Raichel, B. (2013), "Net and prune: A linear time algorithm for Euclidean distance problems", STOC'13: Proceedings of the 45th Annual ACM Symposium on Theory of Computing, pp. 605–614, arXiv:1409.7425.
  5. ^ Gonzalez, T. F. (1985), "Clustering to minimize the maximum intercluster distance", Theoretical Computer Science, 38 (2–3): 293–306, doi:10.1016/0304-3975(85)90224-5, MR 0807927.
  6. ^ a b Har-Peled, S.; Mendel, M. (2006), "Fast construction of nets in low-dimensional metrics, and their applications", SIAM Journal on Computing, 35 (5): 1148–1184, arXiv:cs/0409057, doi:10.1137/S0097539704446281, MR 2217141.
  7. ^ Krauthgamer, Robert; Lee, James R. (2004), "Navigating nets: simple algorithms for proximity search", Proceedings of the 15th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '04), Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, pp. 798–807, ISBN 0-89871-558-X.
  8. ^ Moody, Robert V. (1997), "Meyer sets and their duals", The Mathematics of Long-Range Aperiodic Order (Waterloo, ON, 1995), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, vol. 489, Dordrecht: Kluwer Academic Publishers, pp. 403–441, MR 1460032.
  9. ^ Grünbaum, Branko; Shephard, G. C. (1980), "Tilings with congruent tiles", Bulletin of the American Mathematical Society, New Series, 3 (3): 951–973, doi:10.1090/S0273-0979-1980-14827-2, MR 0585178.

외부 링크