지즈만 플롯
Zisman Plot지스만은 미국의 화학자이자 지구물리학자인 윌리엄 앨버트 지스먼(1905–1986)의 이름을 딴 고체 표면의 습윤성을 특징짓기 위한 지스먼 이론의 그래픽 방법 또는 지스먼 방법을 플롯한다.이것은 고체 표면에 있는 액체 한 방울의 접촉 각도를 기반으로 액체-표면 상호작용을 특징짓는 데 사용되는 유명한 세실 낙하 기법입니다.
지즈만 플롯
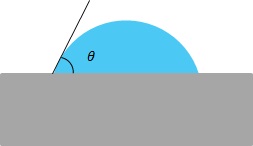
1964년, William Zisman은 ACS 간행물에 "액체와 고체 [1]체질에 대한 평형 접촉각의 관계"에 대한 논문을 발표했다.이 기사에서 그가 오늘날 우리가 지즈만 플롯이라고 부르는 것을 사용한 곳이었습니다.지스만 플롯은 그림 1과 같이 액체 접촉각을 측정하여 고체 표면의 임계 표면장력 θ라고도C 하는 습윤성을 정량적으로 측정하기 위해 사용됩니다.이 각도의 코사인(cosine)을 취하여 고체기판을 적시는 액체의 표면장력에 대해 그래프로 나타내면 임계 표면장력이 발생한다.습윤성은 액체가 얼마나 잘 퍼지고 액체의 접촉이 고체 계면 표면 전체에 얼마나 완전한지를 나타내는 척도입니다.접촉각이 작으면 젖음성이 좋고, 접촉각이 크면 젖음성이 낮음을 나타냅니다.임계 표면 장력은 특정 고체 표면을 완전히 적실 수 있는 가장 높은 액체 표면 장력입니다.접착 접합의 경우 접착 접합 강도를 최대화하기 위해 완전한 습윤이 사용됩니다.
이 관계는 경험적이고 일련의 액체의 표면 장력보다 덜 정밀하지만, 고체 표면의 매개 변수라는 점을 고려할 때 매우 유용합니다.이 방법은 특히 저에너지 고체(주로 플라스틱)의 임계 표면 장력을 매우 빠르고 쉽게 비교 및 측정하는 데 사용됩니다.1964년부터[1] ZIsman이 발표한 논문의 그림 4는 폴리에틸렌의 습윤성 측정값으로 임계 표면 장력을 보여준다.Zisman은 1964년에 이 분석을 발표했으며 그림 4의 x=1의 절편에서 볼 수 있듯이 폴리에틸렌의 임계 표면 장력을 센티미터당 35 다인 정도로 측정하기 위해 다양한 비상동성 액체를 사용했다.1964년[1] Zisman 기사의 그림 12는 테플론, 산 단분자층, 에스테르와 같은 매우 다른 폴리머를 포함한 다양한 플라스틱 기판의 임계 고체 표면 장력을 쉽게 비교할 수 있도록 동일한 그래프에 다른 고형물도 표시할 수 있음을 보여준다.ZIsman Plot은 [2]1960년대 후반 Dann의 작업을 발생시키는 데 도움을 준 고체의 젖음성을 측정하는 매우 효율적인 방법을 가능하게 하는 돌파구임이 입증되었습니다.Dann은 Zisman Plot을 사용하여 다양한 고분자 물질의 임계 표면 장력을 특징짓습니다.현대에는 데이빗과 노이만이 저에너지 [3]표면의 접촉각을 조사했다.그러나 오늘날에는 종속 변수가 액체에 대한 접촉 각도의 코사인이기 때문에 단위 없는 존재이기 때문에 Zisman 그림의 일부 다른 변형이 존재합니다.
현대판 Zisman 플롯 변동
접착제의 경우 접촉 각도로 측정할 수 있는 표면의 습윤은 접착제를 성공적으로 도포하는 데 매우 중요합니다.액체가 얼마나 잘 젖는지 확인하기 위해 고체 표면은 고체 위에 있을 때 액체와의 접촉 각도에 비례합니다.이것은 고체와 액체의 각각의 표면 장력에 의해 결정됩니다.William Zisman이 접착제에 기여한 것은 1-cos(θSL) 대 θL 그래프에 변화가 있는 그의 Zisman 플롯입니다. 이 변화에서 X 절편은 고체 표면을 효과적으로 적시는 데 필요한 액체의 임계 표면 장력을 제공합니다.데이터를 그래프로 그릴 때는 두 가지 단계로 Y축의 0 주위에 있는 모든 점을 무시하고 처음에c ; ;를 찾는 데 가장 적합한 선을 그립니다.0에 가까운 점이 교차로 오른쪽에 착지할 경우, 임계 표면 장력 θ의c 측정을 보다 정확하게 하기 위해 해당 점을 포함하여 회귀를 다시 수행합니다.변수 표와 예는 다음과 같습니다.
변수 표
| 변수 | 묘사 | 단위 |
|---|---|---|
| θSL | 그림 1과 같이 고체에 액체를 떨어뜨리는 각도 | 도 또는 라디안 |
| 1-cos(표준SL) | 습도를 나타내는 Zisman 그림의 Y축 | 유닛리스 |
| γL | 각 액체의 표면 장력 | 다인/cm |
| γC | 고체 기판을 효과적으로 적시는 데 필요한 액체의 임계 표면 장력 | 다인/cm |
예
이 예에서는 표 2(액체 데이터)의 5가지 액체를 사용하여 Zisman 플롯을 사용하여 PC(폴리카보네이트)를 효과적으로 적시는 데 필요한 임계 습윤 표면 장력을 구합니다.
| 리퀴드 넘버 | (X축) 표면장력(다인/cm) | 접촉 각도(도) | (Y축) 1-cos(θSL) |
|---|---|---|---|
| 1 | 27.7 | 10 | 0.0152 |
| 2 | 42.9 | 5 | 0.0038 |
| 3 | 57.2 | 43 | 0.2686 |
| 4 | 64.0 | 50 | 0.3572 |
| 5 | 72.8 | 60 | 0.5000 |
위의 표에서 제시된 액체의 데이터는 독립 변수를 다인/cm 단위의 액체의 표면 장력으로, 종속 변수를 1-cos(θSL)로 지즈만 그림(그림 2)에 그래프로 표시됩니다.또한 표 1과 위에서 언급한 것처럼 Y축은 단위 없음이기 때문에 Zisman 플롯에는 다양한 변형이 있습니다.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
액체 1과 액체 2는 접촉각도가 낮은 것처럼 표면을 완전히 적시기 때문에 PC 표면을 효과적으로 적시는 데 필요한 임계 액체 표면 장력인 θ를C 찾기 위해 가장 적합한 선을 그릴 때 무시해야 합니다. θ는 단순히 지스만 플롯에 가장 적합한 선의 x 절편입니다.최적 적합선을 찾으려면 Microsoft Excel, Minitab, Matlab과 같은 컴퓨터 프로그램을 사용하여 최소 제곱법을 사용하는 것이 좋습니다. 또는 TI-84와 같은 최신 그래프 계산기를 사용하여 최소 제곱법을 수행하는 것도 좋습니다.이는 표 1의 데이터로 이루어졌으며 액체 3, 4, 5의 적합 데이터는 그림 3에서 확인할 수 있다.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
x 절편은 cm당 39.5dynes에 도달합니다(이는 y를 0으로 설정하고 x를 풀어서 계산할 수 있습니다). 따라서 액체 2, cm당 42.9dynes보다 작습니다.PC의 표면을 효과적으로 적시는 데 필요한 임계 액체 표면 장력에 대한 보다 정확한 측정은 그림 4와 같이 최적의 라인을 만들 때 액체 2를 포함시킴으로써 얻을 수 있다.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
여기서 x 절편은 cm당 42.1 다인(y를 0으로 설정하고 x를 풀어서 계산할 수 있음)으로 PC의 임계 액체 표면 장력을 나타냅니다.
요약
오늘날 지즈만 플롯이라고 불리는 것에 대한 윌리엄 지즈만의 공헌은 고체의 습윤성이나 임계 표면 장력을 측정할 수 있는 빠르고 효과적이며 정량적인 방법을 제공함으로써 접착 결합과 표면 화학의 세계에 혁명을 일으켰다.이것은 지난 수십 년 동안 많은 다른 사람들의 작업을 낳았다.1960년대 후반 단의 작품부터 2014년 다비드와 노이만의 작품까지 다양하다.Zisman Plot은 오늘날에도 여전히 사용되고 있으며, Y축은 단위 없이 최신 회귀 소프트웨어 패키지를 사용하여 보다 쉽고 정확하게 찾을 수 있기 때문에 많은 변형이 있습니다.
「 」를 참조해 주세요.
레퍼런스
- ^ a b c ZISMAN, W. A. (1964-01-01). Contact Angle, Wettability, and Adhesion. Advances in Chemistry. Vol. 43. AMERICAN CHEMICAL SOCIETY. pp. 1–51. doi:10.1021/ba-1964-0043.ch001. ISBN 0841200440.
- ^ Dann, J.R (1970). "Forces involved in the adhesive process". Journal of Colloid and Interface Science. 32 (2): 302–320. Bibcode:1970JCIS...32..302D. doi:10.1016/0021-9797(70)90054-8.
- ^ David, Robert; Neumann, A. Wilhelm (2014). "Contact Angle Patterns on Low-Energy Surfaces". Advances in Colloid and Interface Science. 206: 46–56. doi:10.1016/j.cis.2013.03.005. PMID 23601233.
- 지스만, 액체 및 고체 구조에 대한 평형 접촉각의 관계, 1964년 1월 1일, 화학의 진보; 미국 화학 학회:워싱턴 DC, 1964.doi: 10.1021/ba-1964-0043.ch001
- J.R. Dann, 극성 액체에 의한 고분자 고체의 임계 표면 장력, 1969년 9월 16일 콜로이드 및 계면 과학 저널, 제32권, 제2호, 1970년 2월. doi: 10.1016/0021-97979(70)90054-8797
- David와 Neumann, 저에너지 표면의 접촉 각도 패턴, 2013년 3월 26일, 콜로이드 및 계면 과학의 발전, Volume 206, 2014년 4월, Pages 46-56. doi: 10.1016/j.cis.2013.03.005.