관찰자에서 볼 때 두 개의 시선 또는 두 물체 사이의 각도
각도 거리(\ )(각도 분리, 겉보기 거리 또는 겉보기 분리라고도 함)는 관찰자에서 볼 때 두 개의 시선 사이의 각도입니다.
)(각도 분리, 겉보기 거리 또는 겉보기 분리라고도 함)는 관찰자에서 볼 때 두 개의 시선 사이의 각도입니다.
각거리는 수학(특히 기하학과 삼각법)과 모든 자연과학(예: 천문학과 지구물리학)에서 나타난다.회전하는 물체의 고전적인 역학에서, 그것은 각속도, 각가속도, 각운동량, 관성모멘트, 토크와 함께 나타난다.
사용하다
각도 거리(또는 분리)라는 용어는 기술적으로 각도 자체와 동의어이지만, 물체 사이의 선형 거리(예: 지구에서 관측된 두 개의 별)를 암시하는 것을 의미합니다.
측정.
각도 거리(또는 분리)는 개념적으로 각도와 같기 때문에 각도계나 방사선과 같은 동일한 단위로 측정되며, 명확한 방향을 가리키고 해당 각도(예: 망원경)를 기록하도록 특별히 설계된 광학 기기를 사용합니다.
방정식
일반적인 경우

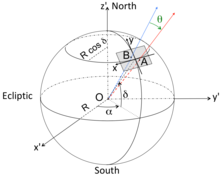
O에서 본 점 A와 B 사이의 각도 간격(\
구체 중심에서 본 구면의 두 점의 각도 간격을 설명하는 방정식을 도출하기 위해 지구에서 관측된 두 와 예를
예를 사용합니다.A(\ A
사용합니다.A(\ A B B는
B B는 천구좌표(RA), B [
천구좌표(RA), B [![{\displaystyle (\alpha _{A},\alpha _{B})\in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a72854b43ba2efa954b8c54fca648a75c441386c) 및 데크레이션(, A에 의해 정의됩니다 __{
및 데크레이션(, A에 의해 정의됩니다 __{![{\displaystyle (\delta _{A},\delta _{B})\in [-\pi /2,\pi /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d268fa7b4324f06ab6279c087cba34c49eb91179) O{\ O는
O{\ O는 천구의 중심에 있다고 가정되는 지구상의 관찰자를 나타냅니다.
천구의 중심에 있다고 가정되는 지구상의 관찰자를 나타냅니다.  의
의 닷 곱은 다음과 같습니다.
닷 곱은 다음과 같습니다.

이는 다음과 같습니다.

, ,) { , )프레임에서는 2개의 유니터리 벡터가 다음과 같이 분해됩니다.
2개의 유니터리 벡터가 다음과 같이 분해됩니다.

그러므로,

그 후, 다음과 같이 합니다.
![{\displaystyle \theta =\cos ^{-1}\left[\sin \delta _{A}\sin \delta _{B}+\cos \delta _{A}\cos \delta _{B}\cos(\alpha _{A}-\alpha _{B})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a1329637b579886c4532f7b13fa3b8a677927b)
작은 각거리 근사
위의 식은 구면상의 A와 B의 위치에 대해 유효하다.천문학에서는 망원경의 시야에 있는 별, 쌍성, 태양계의 거대 행성의 위성 등, 고려 대상 물체가 하늘에 정말로 가까이 있는 경우가 종종 있습니다. A- B1\ \1radian 및 - 1
및 - 1 A B 1 \ style \ _ { - \ _ { } - \ 1 radian the the1 . display style \ delta _ delta \ deltrainfl
A B 1 \ style \ _ { - \ _ { } - \ 1 radian the the1 . display style \ delta _ delta \ deltrainfl  소각 근사에서는 두 번째 순서로 위의 식이 다음과 같이 됩니다.
소각 근사에서는 두 번째 순서로 위의 식이 다음과 같이 됩니다.
![{\displaystyle \cos \theta \approx 1-{\frac {\theta ^{2}}{2}}\approx \sin \delta _{A}\sin \delta _{B}+\cos \delta _{A}\cos \delta _{B}\left[1-{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ee6af02268138ebc119b28d1e0cd07f2509ae6c)
의미.

이런 이유로
- - 2 1 -( A - B ) - A cos ( - ) 2 ( \ { \ { \ ^ { } \ 1 1 - { \ { \ { A } - } } { { } } } } { { { { 2 } } } } ^{ 2 } } } ^{ 2 } ^{ }
전개에서는- B 1 \ \_ { A} - \ _ { - \ 1 1 \ \ _ { } - \ _ { } \ 1 이므로 1이 됩니다 _ \_{ {\{(\{A {} {\_{ {\froxcos } {\frac } } {{{{{B}}}
1이 됩니다 _ \_{ {\{(\{A {} {\_{ {\froxcos } {\frac } } {{{{{B}}}  } } } } } } } 。
} } } } } } } 。
![{\displaystyle \theta \approx {\sqrt {\left[(\alpha _{A}-\alpha _{B})\cos \delta _{A}\right]^{2}+(\delta _{A}-\delta _{B})^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c47a3ad07c626e081b63a368006835cb6f0e99e5)
작은 각도 거리: 평면 근사
 위쪽으로 향하고 자오선에 평행하며이
위쪽으로 향하고 자오선에 평행하며이 편각를
편각를
 따라 평행한 작은 하늘장치수가 1 라디안보다 훨씬 작음을 이미징하는 검출기를 고려할 경우, 각 세파는배율은 다음과 같이 쓸 수 있다.
따라 평행한 작은 하늘장치수가 1 라디안보다 훨씬 작음을 이미징하는 검출기를 고려할 경우, 각 세파는배율은 다음과 같이 쓸 수 있다.

여기서 x (A - B ) cos \ \ x ( \ _ { - \ _ { ) \ \ \ _ { A }
{ A } where where where = B\ style \ y = \ A { A } - \ } - \ delta { A }
where where where = B\ style \ y = \ A { A } - \ } - \ delta { A }
 y축과 동일하지만은
y축과 동일하지만은 cos A\\ _에
cos A\\ _에 변조된 적경입니다.왜냐하면 의
변조된 적경입니다.왜냐하면 의 은 displaystyle의
은 displaystyle의 이기 때문입니다 cosA \ R'\ \ { A }
이기 때문입니다 cosA \ R'\ \ { A }  ( figure figure ) 。
( figure figure ) 。
「 」를 참조해 주세요.
레퍼런스




![{\displaystyle (\alpha _{A},\alpha _{B})\in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a72854b43ba2efa954b8c54fca648a75c441386c)
![{\displaystyle (\delta _{A},\delta _{B})\in [-\pi /2,\pi /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d268fa7b4324f06ab6279c087cba34c49eb91179)


 닷 곱은 다음과
닷 곱은 다음과 




![{\displaystyle \theta =\cos ^{-1}\left[\sin \delta _{A}\sin \delta _{B}+\cos \delta _{A}\cos \delta _{B}\cos(\alpha _{A}-\alpha _{B})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a1329637b579886c4532f7b13fa3b8a677927b)



![{\displaystyle \cos \theta \approx 1-{\frac {\theta ^{2}}{2}}\approx \sin \delta _{A}\sin \delta _{B}+\cos \delta _{A}\cos \delta _{B}\left[1-{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ee6af02268138ebc119b28d1e0cd07f2509ae6c)


![{\displaystyle \theta \approx {\sqrt {\left[(\alpha _{A}-\alpha _{B})\cos \delta _{A}\right]^{2}+(\delta _{A}-\delta _{B})^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c47a3ad07c626e081b63a368006835cb6f0e99e5)

 편각
편각









