안테나 등가 반지름

안테나 도체의 등가 반경은 다음과 같이 정의된다.^[1]^[2]

{\displaystyle r_{e}=\exp \{1\over L^{2}}\}\point _{\ell }\point _{\ell }\ln \vert{\boldsymbol{x}-{\boldsy}-{dx\;dy\right\}}}}}}}}}}}\verturt;di\}}}}}}}}}}}}}}}}}\n \n \cln \vtheat.

여기서 ${\$ $ell$ $}$ 은 $\scriptstyle \ell$ (는 $)$ 도체의 둘레를 나타내며, $\scriptstyle {\boldsymbol {x}}$ ${\$ $\scriptstyle$ $\scriptstyle {x}$ 및 y {\ $displaysty \scriptymbol{\}}}$ 은 $\scriptstyle {L}$ $\scriptstyle {{\boldsymbol {y}}}$ 원주를 따라 위치를 찾는 벡터들이다.ce, $\scriptstyle {dx}$ $\scriptstyle {dx}$ x ${\$ $\scriptstyle {dy}$ $\scriptstyle {dy}$ ${\$ 은(는) 그 위에 있는 차등 세그먼트다 $\scriptstyle {dy}$ . 등가 반지름을 사용하면 균일하고 원형 교차점을 가진 소형 도체에서 생성된 안테나의 분석에는 분석 공식 또는 계산 또는 실험 데이터를 사용할 수 있다. 여기서 "작은"은 단면의 가장 큰 치수가 파장 ${\$ 보다 훨씬 작다는 것을 의미한다 $\scriptstyle {\lambda }$

공식

다음 표에는 1) 모든 치수가 ${\$ 2)보다 훨씬 작으며, 여러 도체로 구성된 단면체의 경우 도체 간 거리가 어떤 단일 도체 차원보다 훨씬 크다. . 사각 및 삼각 단면은 이중 적분(double integrity)의 수치적 평가에 따른다. 다른 모든 공식은 정확하다.

단면도	설명	등가 반지름
	두 개의 동일한 원형 도체	${\sqrt{rs}$
	두 개의 원형 도체 균등하지 않은 반지름으로	$\exp \left\{r_{1}^{2}\ln r_{1}+r_{2}^{2}\ln r_{2}+2r_{1}r_{2}\ln S \over (r_{1}+r_{2}}^{2}}\오른쪽\}}}$
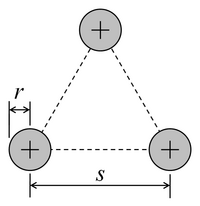	동일 원형 도체 삼각형으로 배열된	$\left(rs^{2}\right)^{1/3}$
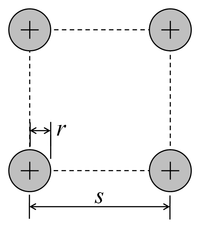	동일 원형 도체 정사각형으로 배열된	$\left\sqrt{2}\,rs^{3}\오른쪽)^{1/4$
	동일 원형 도체 오각형으로 배열된	$\left(2.62\,rs^{4}\오른쪽)^{1/5$
	동일 원형 도체 육각형으로 배열된	$\left(6\,rs^{5}\오른쪽)^{1/6$
	$N$ $N$ 동일한 $N$ 원형 컨덕터 원 둘레에 균일하게 간격을 두고	$\left(NR^{{N-1}\right)^{1/N}$
	평평하고 무한히 얇은 도체	$\displaystyle \displaystyle {We^{-3/2}\ 약 0.22\,W}$
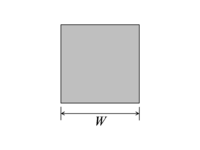	사각도체	$\displaystyle {0.58\,W$
	정삼각형 도체	$\displaystyle {0.41\,W$

파생

등가 반경은 임의 단면 도체 표면의 평균 자기 벡터 전위와 실린더 표면의 전위를 동일시하여 도출한다.

도체의 단면 치수가 파장에 비해 작다고 가정하고, 도체를 따라 전류가 축방향으로 흐를 뿐이며, 도체의 길이를 따라 전류 분포가 서서히 변화하며, 전류가 그 둘레를 따라 대략적으로 균일하게 분포한다고 가정한다(피부 효과에 따라 낮아짐). 더욱이, 도체의 어느 지점 주변 부근에 있는 전류만이 그 지점의 잠재력에 현저하게 기여한다. 시간 의존성은 현재 분포에 시간변동 사인파이를 곱하여 통합될 수 있기 때문에 무시된다. 이러한 조건은 준정전기 조건이 존재하며, 기하학이 사실상 일정한 표면 전류 밀도 $\scriptstyle {Q}$ ${\$ 면적당 전류)를 가진 무한히 긴 도체 중 하나임을 의미하므로, 3차원 문제가 2차원 문제로 감소된다. 또한 자기 벡터 전위가 도체의 축과 평행하다는 것을 암시한다.

먼저 임의 단면 둘레의 고정 $\scriptstyle {\boldsymbol {y}}$ 지점 $\scriptstyle {\boldsymbol {y}}$ ${\$ 에서 가능성을 고려하십시오. 원주를 차등 세그먼트 $\scriptstyle {dx}$ $\scriptstyle {dx}$ ${\$ 로 나눈 상태에서 $\scriptstyle {dx}$ 각각 $\scriptstyle {Q\,dx}$ x ${\$ 길이당 전류)의 선형 밀도를 가진 수직 라인 전류를 각 세그먼트 내에 배치하여 현재 분포의 근사치를 계산할 수 있다. It is well known that the potential of such a line current is $\scriptstyle {-(\mu _{0}Qdx/2\pi )\ln \vert {\boldsymbol {x}}-{\boldsymbol {y}}\vert }$ , where $\scriptstyle {\mu _{0}}$ is the permeability constant. $\scriptstyle {\boldsymbol {y}}$ ${\$ 의 전위는 모든 스트립에 대한 전위의 합으로 다음과 $\scriptstyle {\boldsymbol {y}}$ 같다.

A({\boldsymbol{y}})=-{\mu_{0}Q \over 2\pi \point _{\ell }\ln \vert {\boldsymbol{x}-{\boldsy}\vert;dx.}

평균 잠재력은 그때 이다.

{\bar {A}}={1 \over L}\oint _{\ell }A({\boldsymbol {y}})\;dy\,=-{\mu _{0}Q \over 2\pi L}\oint _{\ell }\oint _{\ell }\ln \vert {\boldsymbol {x}}-{\boldsymbol {y}}\vert \;dx\;dy.

이제 임의 단면의 도체와 동일한 선형 전류 밀도의 실린더의 경우를 고려한다. 또한 평균 전위와 같은 표면의 어느 지점에서도 전위가 존재한다는 것은 잘 알려져 있다.

A_{c}=-{\mu_{0}QL \over 2\pi }\ln \left(r_{e}\오른쪽).

$\scriptstyle {A_{c}}$ 의 ${\$ $\$ $scriptstyle {\bar {A}$ 과 $\scriptstyle {\bar {A}}$ ( $)$ A c {\ $displaystyle$ \ $scriptstyle {A_{$ c $\scriptstyle {A_{c}}$ }}을(를) 동일하게 생성

\ln \left(r_{e}\오른쪽)={1\over L^{2}}\}\point _{\ell }\}\ln \vert {\boldsymbol{x}-{\boldsy}\vert \;dx\;dy\;dy.

양쪽의 지수는 등가 반경의 공식으로 이어진다.

등가 반경의 공식은 일관된 결과를 제공한다. 도체 단면 치수가 계수 $\scriptstyle {\alpha }$ ${\$ 에 의해 스케일링되는 경우 등가 반경은 $\scriptstyle {|\alpha |}$ $displaystyle \scriptstyle{ \alpha }}}.$ 또한 원통형 도체의 등가 반경과 동일하다 $\scriptstyle {|\alpha |}$

참조

^ E.A. Wolff, Antenna Analysis, 3장, John Wiley & Sons, New York, NY, Second Edition, 1966.
^ 데이비드 M. 드럼 셸러 K3WQ, 안테나 등가 반지름: 비원형 도체 모델, QEX, 미국 라디오 릴레이 리그, 뉴링턴 CT, 2017년 3월/4월 10일.

[1] E.A. Wolff, Antenna Analysis, 3장, John Wiley & Sons, New York, NY, Second Edition, 1966.

[2] 데이비드 M. 드럼 셸러 K3WQ, 안테나 등가 반지름: 비원형 도체 모델, QEX, 미국 라디오 릴레이 리그, 뉴링턴 CT, 2017년 3월/4월 10일.

[1]

[2]

Search

안테나 등가 반지름

네임스페이스

더

공식

파생

참조