보조공학

Auxetics
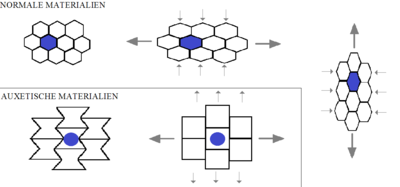
Auxetische Materialien.wiki.png

보조공학은 포아송의 비율이 마이너스인 구조물이나 재료다.늘어나면 가해진 힘에 수직으로 굵어진다.이는 표본이 일직선으로 적재될 때 특정한 내부 구조와 이것이 변형되는 방식 때문에 발생한다.보조공학은 단일 분자, 결정체 또는 거시적 물질의 특정한 구조일 수 있다.[1][2]null

그러한 재료와 구조물은 높은 에너지 흡수율과 파괴 저항성 같은 기계적 특성을 가질 것으로 예상된다.보조 기구는 차체 갑옷,[3] 패킹 재료, 무릎 및 팔꿈치 패드, 강력한 충격 흡수 재료 및 스펀지 마프와 같은 용도에 유용할 수 있다.null

역사

보조라는 용어는 '증가하는 경향이 있는 것'을 뜻하는 그리스어 아우세티코스(αὐξηηις)에서 유래하였으며, '증가'(noun)를 뜻하는 보조(αα)라는 단어에 그 뿌리를 두고 있다.이 용어는 엑세터 대학의 켄 에반스 교수가 만들었다.[4][2]최초의 인공적으로 생산된 보조재료 중 하나인 RFS 구조(다이아몬드 폴드 구조)는 1978년 베를린 연구원 K에 의해 발명되었다.피에츠.비록 보조공학이라는 용어를 사용하지 않았지만, 그는 처음으로 기본 레버 메커니즘과 그것의 비선형 기계적 반응을 보조 네트의 발명자로 간주한다.재료의 부정적인 프와송의 상수와 함께 가장 초기의 출판된 예 AGKolpakov 1985년에,"탄성 프레임워크의 평균 특성의 결정" 했다.;그 다음 합성 생장 촉진의 물질 과학에서는 1987년에는"는 네거티브 프와송비 거품 구조"[1]은 대학 R.S. 호수는에 의해 받을 자격이 묘사되었다 예정이다.w엔콘신 매디슨이다.이 재산을 지칭하기 위해 보조라는 단어를 사용한 것은 아마도 1991년에 시작되었을 것이다.[5]최근에, 세포들은 특정한 조건하에서 생물학적 버전의 보조를 보여주는 것으로 보여졌다.[6]

반전된 육각형 주기성 셀(보정적 육각형)을 가진 합성물의 디자인은 1985년에 출판되었다.[7]null

특성.

전형적으로 보조 재료는 낮은 밀도를 가지고 있는데, 이것이 보조 마이크로 구조의 힌지 같은 영역을 구부릴 수 있게 해주는 것이다.[8]null

거시적 규모에서 보조적 행동은 탄성 코드에 감긴 비탄성 스트링으로 설명할 수 있다.구조물의 끝부분이 분리되면 탄성줄이 늘어나면서 비탄성끈이 곧게 펴지고 그 둘레에 감겨 구조물의 유효 부피가 커진다.매크로스케일에서의 보조적 행동은 Gri마와 Evans가 개발한 보조 회전 삼각형 구조에 기초한 신발과 같은 강화된 특성을 가진 제품의 개발에도 사용될 수 있다.[9][10][11]null

예

신발에서 보조 디자인은 걷거나 뛰면서 발바닥이 넓어지도록 해 유연성을 높인다.

보조 재료의 예는 다음과 같다.

  • 보조[12][13] 폴리우레탄 폼
  • α-크리스토발라이트[14]
  • 회전하는 가로 막대가 있는 액정 중합체는 잠재적으로 보조적일 수 있다.분자 규모로 보조 물질을 생산하기 위한 실험적인 노력은 지금까지 거의 성공하지 못했다.[15]
  • 결정 재료: Li, Na,[16][17][18] K, Cu, Rb, Ag, Fe, Ni, Co, Cs, Cs, Au, Be, Ca, Zn, Sr, Sb, MoS 4 등.
  • 특정 암석 및 광물[19]
  • 공실 결함[20][21] 도입으로 보조적으로 만들 수 있는 그래핀
  • 탄소 다이아몬드 같은 위상[22]
  • 비탄소 나노튜브[23][24]
  • 살아있는 뼈 조직(이것은 의심스러운 것일 뿐)[19]
  • 정상적인 동작 범위 내에 있는 힘줄.[25]
  • 고어텍스와[26] 같은 폴리테트라플루오레틸렌 폴리머의 특정 변형
  • 종이, 몇 가지 유형.종이가 평면 방향으로 늘어나면 네트워크 구조로 인해 두께 방향으로 확장된다.[27][28]
  • 종이접기는 다이아몬드-폴딩-구조물(RFS), 청어뼈-폴드구조물(FFS) 또는 미우라폴드와 같은 여러 종류의 종이접기와 그것에서 파생된 다른 주기적인 패턴으로 접힌다.[29][30][31][32]
직접 레이저 절단을 이용한 패턴 미세구조 절단을 도입하여 보조 메타물질 생산구멍이 뚫린 건축물이 있는 얇은 고무 표면은 구형 표면(오렌지)[33]을 덮고 있다.
  • 특수 설계된 포아송의 비율을 나타내도록 설계된 맞춤형 구조물.[34][35][36][37][38][39]
  • 유기 분자를 사슬로 묶는다.최근의 연구는 n-파라핀과 비슷한 유기 결정체들이 보조적인 행동을 보일 수 있다는 것을 밝혀냈다.[40]
  • 바느질 처리된 부직포.그러한 직물의 네트워크 구조 때문에 열과 압력을 이용한 처리 프로토콜은 일반 (보조기가 아닌) 비와벤을 보조적인 것으로 변환시킬 수 있다.[41][42]
  • 코크는 포아송의 비율이 거의 0이다.이것은 와인병을 밀봉하는데 좋은 재료가 된다.

참고 항목

참조

  1. ^ a b Lakes, R.S. (27 February 1987), "Foam structures with a negative Poisson's ratio", Science, 235 (4792): 1038–40, Bibcode:1987Sci...235.1038L, doi:10.1126/science.235.4792.1038, PMID 17782252, S2CID 21386778.
  2. ^ a b Evans, Ken (1991), "Auxetic polymers: a new range of materials.", Endeavour, 15 (4): 170–174, doi:10.1016/0160-9327(91)90123-S.
  3. ^ "Hook's law". The Economist. 1 December 2012. Retrieved 1 March 2013.
  4. ^ Quinion, Michael (9 November 1996), Auxetic.
  5. ^ Evans, Ken (1991), "Auxetic polymers: a new range of materials", Endeavour, 15 (4): 170–174, doi:10.1016/0160-9327(91)90123-S.
  6. ^ Morrish, RB (2019), "Single Cell Imaging of Nuclear Architecture Changes", Front. Cell Dev. Biol., 7: 141, doi:10.3389/fcell.2019.00141.
  7. ^ Kolpakov, A.G. (1985). "Determination of the average characteristics of elastic frameworks". Journal of Applied Mathematics and Mechanics. 49 (6): 739–745. Bibcode:1985JApMM..49..739K. doi:10.1016/0021-8928(85)90011-5.
  8. ^ 상상력의 확대 – 1997년 6월 7일 – New Scientist Space
  9. ^ Grima, JN; Evans, KE (2000). "Auxetic behavior from rotating squares". Journal of Materials Science Letters. 19 (17): 1563–1565. doi:10.1023/A:1006781224002. S2CID 138455050.
  10. ^ Grima, JN; Evans, KE (2006). "Auxetic behavior from rotating triangles". Journal of Materials Science. 41 (10): 3193–3196. Bibcode:2006JMatS..41.3193G. doi:10.1007/s10853-006-6339-8. S2CID 137547536.
  11. ^ "Nike Free 2016 product press release".
  12. ^ Li, Yan; Zeng, Changchun (2016). "On the successful fabrication of auxetic polyurethane foams: Materials requirement, processing strategy and conversion mechanism". Polymer. 87: 98–107. doi:10.1016/j.polymer.2016.01.076.
  13. ^ Li, Yan; Zeng, Changchun (2016). "Room‐Temperature, Near‐Instantaneous Fabrication of Auxetic Materials with Constant Poisson's Ratio over Large Deformation". Advanced Materials. 28 (14): 2822–2826. doi:10.1002/adma.201505650. PMID 26861805.
  14. ^ Yeganeh-Haeri, Amir; Weidner, Donald J.; Parise, John B. (31 July 1992). "Elasticity of α-Cristobalite: A Silicon Dioxide with a Negative Poisson's Ratio". Science. 257 (5070): 650–652. Bibcode:1992Sci...257..650Y. doi:10.1126/science.257.5070.650. ISSN 0036-8075. PMID 17740733. S2CID 137416819.
  15. ^ Verma, Prateek; He, Chaobin; Griffin, Anselm C. (23 August 2020). "Implications for Auxetic Response in Liquid Crystalline Polymers: X‐Ray Scattering and Space‐Filling Molecular Modeling". Physica Status Solidi B: 2000261. doi:10.1002/pssb.202000261.
  16. ^ Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. (2013). "Classification of cubic auxetics". Physica Status Solidi B. 250 (10): 2038–2043. doi:10.1002/pssb.201384233.
  17. ^ Gorodtsov, V.A.; Lisovenko, D.S. (2019). "Extreme values of Young's modulus and Poisson's ratio of hexagonal crystals". Mechanics of Materials. 134: 1–8. doi:10.1016/j.mechmat.2019.03.017.
  18. ^ Grima-Cornish, JN; Vella-Zarb, L; Grima, JN (2020). "Negative Linear Compressibility and Auxeticity in Boron Arsenate". Annalen der Physik. 532 (5): 1900550. Bibcode:2020AnP...53200550G. doi:10.1002/andp.201900550.
  19. ^ a b Burke, Maria (7 June 1997), "A stretch of the imagination", New Scientist, 154 (2085): 36
  20. ^ Grima, J. N.; Winczewski, S.; Mizzi, L.; Grech, M. C.; Cauchi, R.; Gatt, R.; Attard, D.; Wojciechowski, K.W.; Rybicki, J. (2014). "Tailoring Graphene to Achieve Negative Poisson's Ratio Properties". Advanced Materials. 27 (8): 1455–1459. doi:10.1002/adma.201404106. PMID 25504060.
  21. ^ Grima, Joseph N.; Grech, Michael C.; Grima‐Cornish, James N.; Gatt, Ruben; Attard, Daphne (2018). "Giant Auxetic Behaviour in Engineered Graphene". Annalen der Physik. 530 (6): 1700330. Bibcode:2018AnP...53000330G. doi:10.1002/andp.201700330. ISSN 1521-3889.
  22. ^ Rysaeva, L.Kh.; Baimova, J.A.; Lisovenko, D.S.; Gorodtsov, V.A.; Dmitriev, S.V. (2019). "Elastic properties of fullerites and diamond-like phases". Physica Status Solidi B. 256 (1): 1800049. Bibcode:2019PSSBR.25600049R. doi:10.1002/pssb.201800049.
  23. ^ Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. (2014). "Negative Poisson's ratio for cubic crystals and nano/microtubes". Physical Mesomechanics. 17 (2): 97–115. doi:10.1134/S1029959914020027. S2CID 137267947.
  24. ^ Bryukhanov, I.A.; Gorodtsov, V.A.; Lisovenko, D.S. (2019). "Chiral Fe nanotubes with both negative Poisson's ratio and Poynting's effect. Atomistic simulation". Journal of Physics: Condensed Matter. 31 (47): 475304. Bibcode:2019JPCM...31U5304B. doi:10.1088/1361-648X/ab3a04. PMID 31398716.
  25. ^ Gatt R, Vella Wood M, Gatt A, Zarb F, Formosa C, Azzopardi KM, Casha A, Agius TP, Schembri-Wismayer P, Attard L, Chockalingam N, Grima JN (2015). "Negative Poisson's ratios in tendons: An unexpected mechanical response" (PDF). Acta Biomater. 24: 201–208. doi:10.1016/j.actbio.2015.06.018. PMID 26102335.
  26. ^ Auxetic materials, 9 March 2001.
  27. ^ Baum et al. 1984, Tappi 저널, 외른, O. E.스트레칭에 관한 종이의 두께 변화, Svenesk Papperstidn. 68(5), 141.
  28. ^ Verma, Prateek; Shofner, ML; Griffin, AC (2013). "Deconstructing the auxetic behavior of paper". Physica Status Solidi B. 251 (2): 289–296. Bibcode:2014PSSBR.251..289V. doi:10.1002/pssb.201384243.
  29. ^ Mark, Schenk (2011). Folded Shell Structures, PhD Thesis (PDF). University of Cambridge, Clare College.
  30. ^ Lv, Cheng; Krishnaraju, Deepakshyam; Konjevod, Goran; Yu, Hongyu; Jiang, Hanqing (2015). "Origami based Mechanical Metamaterials". Scientific Reports. 4: 5979. doi:10.1038/srep05979. PMC 4124469. PMID 25099402.
  31. ^ Eidini, Maryam; Paulino, Glaucio H. (2015). "Unraveling metamaterial properties in zigzag-base folded sheets". Science Advances. 1 (8): e1500224. arXiv:1502.05977. Bibcode:2015SciA....1E0224E. doi:10.1126/sciadv.1500224. ISSN 2375-2548. PMC 4643767. PMID 26601253.
  32. ^ Eidini, Maryam (2016). "Zigzag-base folded sheet cellular mechanical metamaterials". Extreme Mechanics Letters. 6: 96–102. arXiv:1509.08104. doi:10.1016/j.eml.2015.12.006. S2CID 118424595.
  33. ^ Mizzi, Luke; Salvati, Enrico; Spaggiari, Andrea; Tan, Jin-Chong; Korsunsky, Alexander M. (2020). "Highly stretchable two-dimensional auxetic metamaterial sheets fabricated via direct-laser cutting". International Journal of Mechanical Sciences. 167: 105242. doi:10.1016/j.ijmecsci.2019.105242. ISSN 0020-7403.
  34. ^ Tiemo Bückmann; et al. (May 2012). "Tailored 3D Mechanical Metamaterials Made by Dip-in Direct-Laser-Writing Optical Lithography". Advanced Materials. 24 (20): 2710–2714. doi:10.1002/adma.201200584. PMID 22495906.
  35. ^ Grima‐Cornish, James N.; Grima, Joseph N.; Evans, Kenneth E. (2017). "On the Structural and Mechanical Properties of Poly(Phenylacetylene) Truss-Like Hexagonal Hierarchical Nanonetworks". Physica Status Solidi B. 254 (12): 1700190. Bibcode:2017PSSBR.25400190G. doi:10.1002/pssb.201700190. hdl:10871/31485. ISSN 1521-3951.
  36. ^ Cabras, Luigi; Brun, Michele (2014). "Auxetic two-dimensional lattices with Poisson's ratio arbitrarily close to −1". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 470 (2172): 20140538. arXiv:1407.5679. Bibcode:2014RSPSA.47040538C. doi:10.1098/rspa.2014.0538. ISSN 1364-5021.
  37. ^ Carta, Giorgio; Brun, Michele; Baldi, Antonio (2016). "Design of a porous material with isotropic negative Poisson's ratio". Mechanics of Materials. 97: 67–75. doi:10.1016/j.mechmat.2016.02.012.
  38. ^ Cabras, Luigi; Brun, Michele (2016). "A class of auxetic three-dimensional lattices". Journal of the Mechanics and Physics of Solids. 91: 56–72. arXiv:1506.04919. Bibcode:2016JMPSo..91...56C. doi:10.1016/j.jmps.2016.02.010. S2CID 85547530.
  39. ^ Kaminakis, N; Stavroulakis, G (2012). "Topology optimization for compliant mechanisms, using evolutionary-hybrid algorithms and application to the design of auxetic materials". Composites Part B Engineering. 43 (6): 2655–2668. doi:10.1016/j.compositesb.2012.03.018.
  40. ^ Stetsenko, M (2015). "Determining the elastic constants of hydrocarbons of heavy oil products using molecular dynamics simulation approach". Journal of Petroleum Science and Engineering. 126: 124–130. doi:10.1016/j.petrol.2014.12.021.
  41. ^ Verma, Prateek; Lin, A; Wagner, KB; Shofner, ML; Griffin, AC (2015). "Inducing out-of-plane auxetic behavior in needle-punched nonwovens". Physica Status Solidi B. 252 (7): 1455–1464. Bibcode:2015PSSBR.252.1455V. doi:10.1002/pssb.201552036.
  42. ^ Verma, Prateek; Shofner, Meisha L.; Lin, Angela; Wagner, Karla B.; Griffin, Anselm C. (2016). "Induction of auxetic response in needle-punched nonwovens: Effects of temperature, pressure, and time". Physica Status Solidi B. 253 (7): 1270–1278. Bibcode:2016PSSBR.253.1270V. doi:10.1002/pssb.201600072. ISSN 1521-3951.

외부 링크