백점핑
Backjumping역추적 알고리즘에서 백점핑은 검색 공간을 줄여 효율을 높이는 기술이다.변수에 대한 모든 값을 테스트했을 때 역추적이 항상 검색 트리에서 한 레벨 위로 올라가는 반면, 역점프는 더 높은 레벨로 올라갈 수 있다.이 글에서는 변수 , n 의 고정된 평가 순서가 사용되지만, 동적인 평가 순서에도 동일한 고려 사항이 적용된다.
정의
역추적이 아무런 해결책도 찾지 못한 채 변수에 대한 모든 값을 시도했을 때마다 이전에 할당된 변수의 마지막 값을 재고하여 다른 값을 시도하지 않을 경우 값을 변경하거나 추가 역추적을 한다.If is the current partial assignment and all values for have been tried without finding a solution, backtracking concludes that no solution extending 이(가) 존재한다.그런 다음 알고리즘이 로 "위로 이동"하고 가능하면 의값을 변경하고, 그렇지 않으면 다시 역추적한다.
+ 의 값이 솔루션으로 이어지지 않는다는 것을 입증하기 위해 부분 배정은 항상 완전히 필요한 것은 아니다.특히 부분 과제의 접두사가 같은 속성이 있을지 몰라도, 그, 색인 j<>k{\displaystyle j<, k}가 x1,…,)j)1,…, j{\displaystyle x_{1},\ldots ,x_{j}=a_{1},\ldots ,a_{j}}x에 어떠한 값을 갖고 있는 해결책을 만들기 위해 확장될 수 없k+1{존재한다.\disp알고리즘이 이 사실을 증명할 수 있다면, 처럼 xk {\를 재고하는 대신 x x_에 대해 다른 값을 직접 고려할 수 있다.
백점프 알고리즘의 효율성은 백점프가 가능한 높이에 따라 달라진다.이상적으로는 알고리즘이 + 에서 x , 에 대한 전류 할당을 확장하여 k+ 의 값을 가진 솔루션을할 수 없는 변수 j {\displaystystyle 로 할 수 있다이 경우 을(를) 세이프 점프라고 한다.
안전 점프는 알고리즘이 찾으려고 하는 해결책의 측면에서 정의되기 때문에 점프가 안전한지 여부를 확인하는 것이 항상 가능한 것은 아니다.실제로 백점프 알고리즘은 안전 점프를 증명할 수 있는 가장 낮은 지수를 사용한다.다른 알고리즘은 점프가 안전한지 여부를 결정하기 위해 다른 방법을 사용한다.이러한 방법은 비용은 다르지만, 검색 트리의 일부를 건너뛰어 검색량을 줄일 수 있기 때문에 더 높은 안전 점프를 찾는 비용이 발생할 수 있다.
리프 노드에서 백점핑
백점핑이 가능한 가장 간단한 조건은 변수의 모든 값이 더 이상 분기되지 않고 일관성이 없다는 것이 입증된 경우다.제약조건 만족도에서 부분평가는 할당된 변수와 관련된 모든 제약조건을 만족하는 경우에만 일관되고, 그렇지 않으면 일관성이 없다.할당되지 않은 변수 중 일부는 다른 제약조건을 위반하지 않고 할당되지 않을 수 있기 때문에 일관성 있는 부분적인 해결책이 일관된 완전한 해결책으로 확장될 수 없는 경우가 있을 수 있다.
주어진 변수 + 1 의 모든 값이 현재의 부분 솔루션 1, k = ,, x_의 모든 값이 잎 막다른 골목이라고 한다.이는 변수 + 이 검색 트리의 한 잎일 때 정확히 발생한다(이 글의 그림에서 자식으로만 남겨진 노드에 해당한다).
가스니그의 백점프 알고리즘은 잎 막다른 골목에서만 백점프를 한다.즉, 다른 변수에 할 없이 x + 1 의 모든 가능한 값을 테스트하여 일관성이 없는 결과를 얻었을 때만 역추적과 다르게 작용한다.
A safe jump can be found by simply evaluating, for every value , the shortest prefix of inconsistent with .즉, + 이 k+ 에 대해 가능한 값이라면 알고리즘은 다음과 같은 평가의 일관성을 확인한다
| ... | ||||
| ... | ||||
| ... | ||||
+ = + a_{k+1}에 대해 가능한 유일한 값이 x + 1 }일 경우 평가가 일관되지 않는 가장 작은 지수(목록이 가장 낮음)가 안전한 점프일 것이다모든 변수는 보통 둘 이상의 값을 취할 수 있기 때문에 각 값에 대한 점검에서 나오는 최대 지수는 안전점프(safe jump)이며, 가스니그의 알고리즘이 점프를 하는 지점이다.
알고리즘은 x + 1= + 의 일관성을 확인하는 동시에 위의 평가를 확인할 수 있다
내부 노드에서의 백점핑
이전 알고리즘은 추가 분기 없이 변수의 값이 현재의 부분 솔루션과 일치하지 않는 것으로 나타날 때에만 백점프한다.즉, 검색 트리의 리프 노드에서만 백점프를 허용한다.
검색 트리의 내부 노드는 이전 노드와 일치하는 변수의 할당을 나타낸다.이 할당을 확장하는 솔루션이 없는 경우 이전 알고리즘은 항상 백트랙: 이 경우에는 백점프가 수행되지 않는다.
leaf 노드의 경우 내부 노드에서 백점핑을 수행할 수 없다.실제로 + 의 일부 평가에서 분기가 필요했다면, 이는 현재 과제와 일치하기 때문이다.따라서 마지막 변수의 이러한 값과 일치하지 않는 접두사를 검색하는 것은 성공하지 못한다.
이러한 에 평가 + 1= + +1}=a_{k 현재 부분평가 , 는 재귀적 검색이다.특히 알고리즘은 솔루션을 찾은 후 정지하지 않고 이 노드로 돌아오기 때문에 이 시점부터 솔루션이 존재하지 않는다는 것을 '알고 있다'는 것이다.
이러한 복귀는 알고리즘이 부분적인 해결책의 일관성이 없는 것으로 입증된 다수의 막다른 점 때문이다.백점프를 더 진행하기 위해서는 알고리즘이 이러한 막다른 골목에 기인하는 해결책 찾기가 불가능하다는 점을 고려해야 한다.특히, 안전 점프는 여전히 이러한 막다른 골목들을 일관되지 않는 부분적인 해결책으로 만드는 접두사의 지수들이다.
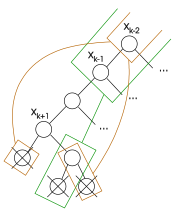
즉, k+ 의 모든 값을 시도했을 때 알고리즘은 x ,, x ,x i {\ x_,x_의 현재 진실 평가가 모든 진실 평가와 일관되지 않는다면 이전 변수 로 역점프할 수 있다.노드 + 의 하위인 리프 노드에서
단순화
+ 의 하위 트리에 있는 잠재적으로 많은 수의 노드 때문에 트리를 방문하는 동안 x + 로부터 안전하게 백점프하는 데 필요한 정보가 수집된다.안전한 점프를 찾는 것은 두 가지 고려사항으로 단순화할 수 있다.첫 번째는 알고리즘이 안전한 점프가 필요하지만 여전히 가능한 가장 높은 안전 점프가 아닌 점프로 작동한다는 점이다.
두 번째 단순화는 에서 건너뛴 x {\의 하위 트리에서 x 에 대한 백점프를 찾는 동안 무시될 수 있다는 것이다 더 정확히 말하면, 모든 가x m {\에서 x }까지 백점프로 건너뛴다.은는) {\ x_에 뿌리를 둔 하위 트리와는 무관하며 다른 하위 트리도 관련이 없다.
실제로 알고리즘이 경로를 통해 노드 x 에서 x 로 내려갔지만 돌아오는 길에 백점프(backjump)로 내려갔다면 에서 m 로 바로 내려갔을 수 있다.실제로 백점프(는 x l {\ 와 x m {\displaystyle 사이의 가 x m {\displaystyle 에 뿌리를 둔 하위 트리와 무관함을 나타낸다 즉, 백점프(backjump)는 검색 트리의 한 지역을 방문한 것이 실수였음을 나타낸다. 트리의 이 부분은 x l 또는 그 조상 중 하나에서 발생할 수 있는 백점프를 고려할 때 무시될 수 있다.
이러한 사실은 각 노드에서 이전에 할당된 변수 집합을 수집하여 이용할 수 있으며, 이러한 변수들은 평가만으로 노드에 뿌리를 둔 하위 트리에 해결책이 존재하지 않음을 증명할 수 있다.이 세트는 알고리즘 실행 중에 구축된다.노드에서 수축할 때, 이 세트는 노드의 변수를 제거하고 역추적 또는 역점프의 목적지 집합에 수집된다.백점프에서 건너뛰는 노드는 절대 물러나지 않기 때문에 노드의 세트는 자동으로 무시된다.
그래프 기반 백점핑
그래프 기반 백점핑의 근거는 , k 중 변수가 x + , k+ 2,.. . . . . displaystyle . . . . . . . . . . x_x_x_x_{k+1}, .leaf 노드에서 인스턴스화된}.서 인스턴스화하는 지수 > k 의 모든 리프 노드와 모든 변수 에 대해 변수가 i 로 제약되는 보다 작거나 같은 인덱스를 사용하여 안전한 점프를 찾을 수 있다.특히 x + 의 모든 값을 사용해 본 세트에는 x + 1 에 뿌리를 둔 하위 트리를 방문하여 어떠한 해결책도 찾을 수 없음을 평가할 수 있는 변수들의 인덱스가 수록되어 있다결과적으로 알고리즘은 이 집합에서 가장 높은 지수로 역점프할 수 있다.
백점프(backjumping)로 건너뛴 노드가 추가 백점프를 고려할 때 무시될 수 있다는 사실은 다음 알고리즘에 의해 악용될 수 있다.리프 노드에서 수축할 때, 그것과 제약이 있는 변수들의 집합이 만들어지고 백점핑의 경우 그것의 부모 또는 조상에게 "뒤로" 보내진다.모든 내부 노드에서는 일련의 변수가 유지된다.변수 집합이 자식 또는 자손 중 하나로부터 수신될 때마다 변수 집합이 유지 관리 집합에 추가된다.노드에서 추가 역추적 또는 역점핑 시 노드의 변수가 이 세트에서 제거되고, 역추적 또는 역점핑의 목적지인 노드로 세트가 전송된다.이 알고리즘은 노드에서 유지되는 세트가 이 노드의 후예인 잎에서 불만족성을 증명하는 데 관련된 모든 변수를 수집하기 때문에 작동한다.변수 집합은 노드에서 재추적할 때만 전송되기 때문에 백점핑으로 건너뛴 노드에서 수집된 집합은 자동으로 무시된다.
충돌 기반 백점핑(일명 충돌 방향 백점핑(cbj))
때로는 더 큰 백점프를 달성할 수 있는 여전히 더 정교한 백점프 알고리즘은 동일한 제약조건에서 두 변수의 공통적인 존재 여부뿐만 아니라 제약조건이 실제로 불일치를 유발했는지를 확인하는 것에 기초한다.특히 이 알고리즘은 모든 잎에서 위반된 제약조건 중 하나를 수집한다.모든 노드에서, 나뭇잎에서 수집된 제약조건 중 하나에 있는 변수의 가장 높은 지수는 안전한 점프다.
각 잎에서 선택한 위반 제약조건은 결과 점프의 안전성에 영향을 미치지 않지만, 가능한 가장 높은 지수의 제약조건을 선택하면 점프의 전하가 증가한다.이러한 이유로, 하위 지수 변수에 대한 제약조건이 상위 지수 변수에 대한 제약조건보다 선호되는 방식으로 갈등 기반 백점핑 주문 제약조건이 선호된다.
형식적으로 에서 변수의 최고 지수가 에서보다 낮지만 에서는 그렇지 않은 경우 보다 제약조건 C {\displaystytyle C이 더 선호된다. 즉, exc.공통 변수 루딩으로, 모든 낮은 지수를 가지는 제약조건이 선호된다.
리프 노드에서 은 1,…, 와 같은 가장 낮은 지수 를 선택한다.이 평가에서 위반되는 제약조건 중에서 가장 선호하는 것을 선택하고, 보다 작은 모든 지수를 한다이렇게 해서 알고리즘이 변수 x + 1 에 되돌아오면 가장 낮은 수집 지수는 안전한 점프를 식별한다
실제로 이 알고리즘은 의 모든 값에 대해 세트를 생성하는 대신 단일 세트의 모든 지수를 수집함으로써 단순화된다 특히 알고리즘은 각 노드에서 백점핑으로 건너뛰지 않은 모든 세트를 수집한다.이 노드에서 수축할 때, 이 세트는 노드의 변수를 제거하고 역추적 또는 역점프 목적지로 수집된다.
갈등주도형 백점프는 패트릭 프로서(Patrick Prosser)가 1993년 발표한 논문에서 '제약 만족도 문제'를 위해 제안했다.
참고 항목
참조
- Dechter, Rina (2003). Constraint Processing. Morgan Kaufmann. ISBN 1-55860-890-7.
- Prosser, Patrick (1993). "Hybrid Algorithms for the Constraint Satisfaction Problem" (PDF). Computational Intelligence 9(3).





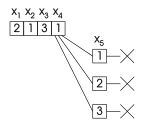












 모든 값이 잎 막다른 골목이라고 한다.이는 변수
모든 값이 잎 막다른 골목이라고 한다.이는 변수 















 x
x 


 변수의 최고 지수가
변수의 최고 지수가 




