베테 공식

이 글에는 아마도 독창적인 연구가 포함되어 있을 것이다. 클레임을 확인하고 인라인 인용문을 추가하여 개선하십시오. 원본 연구로만 구성된 문장은 제거해야 한다. (2020년 10월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

Bethe 공식 또는 Bethe-Bloch 공식은 빠르게 충전된 입자(프로톤, 알파 입자, 원자 이온)를 통과하는 물질(또는 물질의 정지 출력)의 이동 거리당 평균 에너지 손실을 설명한다^[1].전자의 경우 에너지 손실은 작은 질량(상대론적 보정을 필요로 함)과 그 구별하기 어려운 가능성 때문에 약간 다르며, 브렘스스트라훌룽에 의해 훨씬 더 큰 손실을 입기 때문에 이를 설명하기 위해 항을 추가해야 한다.물질을 통해 이동하는 빠르게 충전된 입자는 물질 내 원자의 전자와 상호작용을 한다.그 상호작용은 원자를 흥분시키거나 이온화시켜, 이동 입자의 에너지 손실을 초래한다.

비 상대적 버전은 1930년 한스 베테에 의해 발견되었고, 상대적 버전(아래에 표시)은 1932년에 그에 의해 발견되었다.^[2]가장 가능성이 높은 에너지 손실은 평균 에너지 손실과 다르며 란다우-바빌로프 분포로 설명된다.^[3]

공식

속도 v, 전하 z(전자 전하의 배수로), 에너지 E가 거리 x를 전자 수 밀도 n과 평균 흥분 전위 I로 이동하는 경우, 공식의 상대론적 버전은 SI 단위로 다음과 같다.^[2]

${\displaystyle -\left\langle {\frac {dE}{dx}}\right\rangle ={\frac {4\pi }{m_{e}c^{2}}}\cdot {\frac {nz^{2}}{\beta ^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{e}c^{2}\beta ^{2}}{I\cdot (1-\beta ^{2}}}\오른쪽)-\beta ^{2}\오른쪽]}$

(1)

여기서 c는 빛의 속도, ε₀ 진공 허용률, $\beta {\displaystyle }$= v ${\displaystyle \frac{c}{}}$ ${\$c$\}\},$ e 및 m_e 각각 전자 전하와 휴식 질량이다.

여기서 물질의 전자 밀도는 다음과 같이 계산할 수 있다.

${\displaystyle n={\frac {N_{A}\cdot Z\cdot \rho }{A\cdot M_{u}}}\...}$

여기서 ρ은 물질의 밀도, Z 원자 번호, A 상대 원자 질량, N 아보가드로_A 번호, M_u 몰라 질량 상수이다.

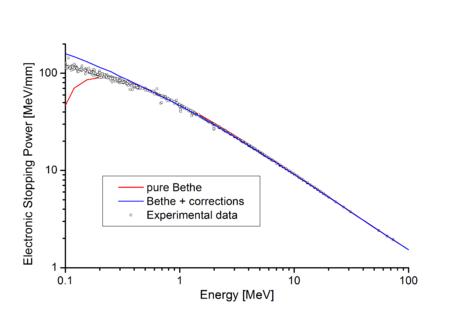
오른쪽 그림에서 작은 원은 다양한 저자의 측정에 의해 얻은 실험적인 결과인 반면, 빨간색 곡선은 베테의 공식이다.^[4]분명히, 베티의 이론은 높은 에너지에서의 실험과 매우 잘 일치한다.수정이 적용될 때(아래 참조) 합의는 더욱 좋다.

낮은 에너지, 즉 입자 β << 1>의 작은 속도의 경우 베테 공식은 다음과 같이 감소한다.

${\displaystyle -{\frac {dE}{dx}}={\frac {4\pi nz^{2}}{m_{e}v^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{e}v^{2}}{I}\right)\right].}$

(2)

이는 eq. (1)에서 βc를 v로 먼저 교체한 다음 크기가 작기 때문에 β를² 무시하는 것으로 볼 수 있다.

따라서 낮은 에너지에서 베테 공식에 따른 에너지 손실은 에너지가 증가할 때 대략 v만큼⁻² 감소한다.대략 E = 3Mc에² 대해 최소치에 도달하며, 여기서 M은 입자의 질량이다(양자의 경우 약 3000MeV).상대성이 높은 사례 β β 1의 경우, 에너지 손실이 다시 증가하며, 로그상으로 전기장의 횡단적 구성요소로 인해 증가한다.

평균 흥분 전위

베테 이론에서 물질은 하나의 숫자, 즉 평균 흥분 가능성 I로 완전히 설명된다.1933년에 Felix Bloch는 원자의 평균 이온화 잠재력은 대략 에 의해 주어진다는 것을 보여주었다.

${\displaystyle I=(10~\mathrm {eV} )\cdot Z}$

(3)

여기서 Z는 물질 원자의 원자 번호다.위의 식 (1)에 이 근사치를 도입하면 흔히 베테-블록 공식이라고 하는 식을 얻게 된다.그러나 이제 우리는 Z의 함수로서 I의 정확한 표를 갖게 되었기 때문에(아래 참조), 그러한 표를 사용하면 공식 (3)의 사용보다 더 좋은 결과를 얻을 수 있을 것이다.

그림은 표에서 추출한 I의 정규화된 값을 보여준다.^[5]이 그림의 봉우리와 계곡은 정지력의 해당 계곡과 봉우리로 이어진다.이를 "Z-oscillation₂" 또는 "Z-structure₂"라고₂ 한다(여기서 Z = Z는 목표물의 원자 번호를 의미한다).

베테 공식 수정

베테 공식은 충전된 원자 입자(이온)가 원자 전자를 가지고 다니지 않을 정도로 충분히 높은 에너지에만 유효하다.작은 에너지에서, 이온이 전자를 운반할 때, 이것은 효과적으로 전하를 감소시키고, 따라서 정지력을 감소시킨다.그러나 원자가 완전히 이온화되더라도 보정이 필요하다.

베티는 양자역학 섭동 이론을 이용하여 그의 공식을 찾았다.따라서 그의 결과는 입자의 전하 z의 제곱에 비례한다.보다 높은 z의 힘에 해당하는 보정을 고려하여 설명을 개선할 수 있다.바카스-안데르센 효과(Walter H. Barkas 및 Hans Henrik Andersen 다음으로 z에³ 비례), 블로흐 보정(z에⁴ 비례) 등이 그것이다.또한, 통과된 물질의 원자 전자가 정지해 있지 않다는 것("껍질 보정")도 고려해야 한다.

예를 들어, 양성자와 알파 입자의 정지 전력을 계산할 수 있는 PSTAR와 ASTAR 프로그램에 언급된 수정 사항이 내장되어 있다.^[6]낮은 에너지에서는 보정이 크고 에너지가 증가함에 따라 점점 작아진다.

매우 높은 에너지에서는 페르미의 농도 보정도^[5] 추가되어야 한다.

참고 항목

• 정지 전원(입자 방사선)
• 란다우 분포
• 한스 베테

참조

외부 링크

• 스트래글링 함수.전하 입자의 에너지 손실 분포
• 원본 출판물: "Annalen der Physik"의 Jur Theory des Durchgangs Schneller Korpuskularstrahlen durch Matterie, 397 (1930) 325 -400
• 전하를 띤 입자가 물질을 통과하는 그래프
• 양성자 및 알파 입자의 정지 전원
• 전원 그래프 및 데이터 중지
• 최근 숫자 솔루션