이항 질량 함수

천문학에서 쌍성질량함수(binary mass function) 또는 단순히 질량함수(mass function)는 보이지 않는 구성요소(일반적으로 별 또는 외부 행성)의 질량을 단일 선 분광 쌍성 또는 행성계에서 구속하는 함수이다.이 값은 관측 가능한 양, 즉 쌍성계의 공전 주기 및 관측된 별의 최대 반지름 속도로만 계산할 수 있습니다.한 쌍성분의 속도와 궤도 주기는 두 성분 사이의 분리 및 중력, 즉 성분의 질량에 대한 (제한적인) 정보를 제공합니다.

서론

이항질량함수는 케플러의 세 번째 법칙에 따라 하나의 (관측된) 쌍성분 반지름 속도가 ^[1]도입됩니다.케플러의 제3법칙은 두 물체가 공통 질량 중심을 도는 운동을 묘사한다.이는 궤도 주기(한 궤도를 완전히 도는 데 걸리는 시간)와 두 물체 사이의 거리(궤도 분리) 및 질량의 합과 관련이 있습니다.주어진 궤도 분리의 경우, 총계 질량이 클수록 궤도 속도가 더 빨라집니다.반면에, 주어진 시스템 질량에 대해, 긴 궤도 주기는 더 큰 분리 및 낮은 궤도 속도를 의미합니다.

바이너리 시스템의 궤도 주기 및 궤도 속도는 바이너리 성분의 질량과 관련이 있기 때문에 이들 파라미터를 측정하면 하나 또는 두 ^[2]성분의 질량에 대한 정보를 얻을 수 있습니다.그러나 실제 궤도 속도는 일반적으로 결정될 수 없기 때문에 ^[1]이 정보는 제한적입니다.

반지름 속도는 관측자의 시선에서의 궤도 속도의 속도 성분이다.실제 궤도 속도와는 달리,^[3] 반지름 속도는 별의 빛에 의한 스펙트럼 라인의 도플러 분광법이나 전파 ^[4]펄서로부터의 펄스의 도착 시간의 변화로부터 결정될 수 있다.두 개의 쌍성분 중 하나의 반경 운동만 측정할 수 있는 경우 쌍성계를 단일선 분광 쌍성계라고 합니다.이 경우 다른(보이지 않는) 성분의 질량에 대한 하한을 ^[1]결정할 수 있다.

실제 질량과 실제 궤도 속도는 일반적으로 궤도 기울기를 알 수 없기 때문에 반경 속도로부터 결정될 수 없다. (경사각은 관찰자의 관점에서 본 궤도의 방향이며, 실제와 반경 속도와 관련이 있다.)^[1]이것은 질량과 ^[5][6]기울기 사이의 퇴화를 일으킨다.예를 들어 측정된 반지름 속도가 낮으면 실제 궤도 속도가 낮고(낮은 질량의 물체를 포함), 기울기가 높거나(궤도가 가장자리에 위치), 또는 실제 속도가 높지만(높은 질량의 물체를 포함), 기울기가 낮음을 의미할 수 있습니다(궤도가 정면).

원형 궤도에 대한 유도

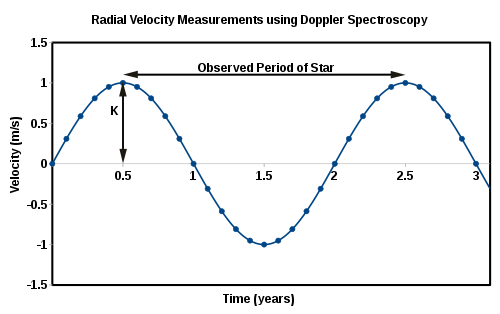
피크 $반지름{\displaystyle }$ 속도$$K(\$displaystyle$K)는$$ 그림과 같이 반지름 속도 곡선의 반진폭입니다.궤도 $주기{\displaystyle {}_{}}$ ${\displaystyle {P\mathrm{}}_{}}$ ${\displaystyle {\mathrm{o}}_{}}$ r$$ {$style P_{\mathrm {orb}}$는 반경 속도 곡선의 주기성으로부터 구한다.이 두 양은 이항 ^[2]질량 함수를 계산하는 데 필요한 두 가지 관측 가능한 양입니다.

이 기사에서 반경 속도를 측정할 수 있는 관찰된 물체는 물체 1로 간주되며, 보이지 않는 동반물은 물체 2이다.

${\displaystyle {M\mathrm{}}_{}}$ 1$({$ 및$$ ${\displaystyle {M\mathrm{}}_{}}$2({$displaystyle M_{2})$를 별의 질량으로 $합니다{\displaystyle {}_{}}$. ${\displaystyle {M\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$+ ${\displaystyle {M\mathrm{}}_{}}$ 2 $=$ ${\displaystyle {M\mathrm{}}_{}}$ ${\displaystyle {\mathrm{t}}_{}}$ t({$displaystyle M_{1$} + $M_{2$}= $M_$${\mathrm {t}$} = $2진법계$의 총 질량, ${\displaystyle {v\mathrm{}}_{}}$ 1$${$displaystyle$ ${\displaystyle {v\_1\mathrm{}}_{}}$$}$ $및$ 2$}$ } 。$1$(디스플레이 스타일 a_${1})$ $및$ $($ 스타일 $a_{2})$ 질량$$ 중심까지의 물체 거리. $a{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$+ ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ $=$ ${\displaystyle a}$ {\$디스플레이$ 스타일 $a_{$1} +$a_{2$$}=$a$$}는 이항계의 반장축(원형 분리)입니다.

먼저 케플러의 제3법칙 ${\displaystyle {r\mathrm{}}_{}}$ ${\displaystyle \mathrm{o}}$ ${\displaystyle {\mathrm{r}}_{}}$ b ${\displaystyle {=}_{}}$ ${\displaystyle 2{}_{}}$ ${\displaystyle /}$ / ${\displaystyle {P\mathrm{}}_{}}$ ${\displaystyle {\mathrm{o}}_{}}$ r$$b { $displaystyle$\ $omega$_ { \ $mathrm {$ orb } =$2 \pi$ / P_{ \ $mathrm {$ orb$$$$} } } } orb $및{\displaystyle }$ G { \$$displaystyle G$$} 로 시작합니다.

${\displaystyle GM_{\mathrm {tot}}=\omega_{\mathrm {orb}^{2}a^{3}.}$

질량 위치의 중심인 $M{\displaystyle {}_{}}$ ${\displaystyle {}_{}{}_{}}$ a ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {a\mathrm{}}_{}}$2 { { $displaystyle M_{1} a_${1} =$M_{$2}$a_{$2$\}\}$^[1]의 정의를 사용하여 다음과 같이 쓸 수 있습니다.

${\displaystyle a=a_{1}+a_{2=a_{1}\left(1+{\frac {a_{1}}\right)=a_{1}\left(1+{\frac {M_{1}}{{{2}}\right)=black {a_{1}\frac {a_{2}}(M_{1}\right)={{1}\frac {{1}\frac {{{{1}}}{{{{}}}}}}}}{{{}}}}}}}}}{{{{}}}}}}}}}}}}}}}}}}}}$

$이$ 표현식을$$케플러의$$제3법칙에 삽입하면

${\displaystyle GM_{\mathrm {tot}}=\mathrm {orb}^{2}{\frac {a_{1}^3}M_{\mathrm {tot} }^{3}} {M_{2}^{3}}}.}$

다시 쓸 수 있다

${{displaystyle {M_{2}^{3}}{M_{\mathrm {tot}^{2}={frac {ob}{2}a_{1}^3}}{G}}.$

물체 $1$의 최대 반지름 속도 K$(\displaystyle$K$)$는 궤도$기울기$ i(\$displaystyle$ i$)$에 따라 달라집니다(0°의 기울기는 정면으로 본 궤도에 해당하고 90°의 기울기는 가장자리로 본 궤도에 해당합니다).원형 궤도의 경우(이심률 = 0)는^[7] 다음과 같다.

${\displaystyle K=v_{1}\mathrm {sin} i=\omega_{\mathrm {orb} a_{1}\mathrm {sin} i.}$

1$({$을 치환한 결과,

${{displaystyle {M_{2}^{3}}{M_{\mathrm {tot}^{2}}={K^{3}}{G\mathrm {orb}\mathrm {sin}^{3}i}}}.}$

2진수 $질량{\displaystyle }$ 함수$$f\$displaystyle$ f$($질량 단위 포함)는^{[8][7][2][9][1][6][10]}

${{displaystyle f=param {M_{2}^{3}\mathrm {sin}^{3}i}{(M_{1}+M_{2}^2}}=param {P_{\mathrm {orb}}\K^{3}}{2\pi G}}}.$

관측물체 1의 $추정질량{\displaystyle {}_{}}$$또는$ 가정질량 ${\displaystyle {\mathrm{M1}}_{}}$({$displaystyle$ $M_{1})$에 대하여 i ${\displaystyle =}$ ${\displaystyle {90}^{}}$µ {$displaystyle$$$i$=90^{\$$mathrm$$${2,$min}}}}}$ $\}$ . $i{\displaystyle }$ i i i i i assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming assuming${\displaystyle {}_{}}$assuming ${\displaystyle {\mathrm{assuming}}_{}}$ assuming assuming assuming assuming ${\displaystyle {\mathrm{assuming}}_{}}$ assuming assuming assuming$실제{\displaystyle {}_{}}$ 질량 $({$displaystyle $M_{2})$는 궤도 기울기에 따라 달라집니다.물매는 일반적으로지만 어느 정도에 관찰된 eclipses,[2]에서 또는 타원체의 변화를 사용하여 빚은 조각품이 되eclipses,[8][9](2진법에서는 별의non-spherical 모양 밝기에서 system'에 의존하는 궤도의 과정에 걸쳐 변화에 이르게 하는 것의 그 non-observation으로부터 무리할 결정될 수 있다 알려져 있지 않다.sinclination)^[11]

한계

${\displaystyle {M\mathrm{}}_{}}$ 1${\displaystyle {}_{}{}_{}}$ M$$ {\$displaystyle M_{1}\gg$ M_${2}}$의 경우(예를 들어 보이지 않는 물체가 외계^[8] 행성인 경우) 질량 함수는 다음과 같이 단순화된다.

${\displaystyle f\approx {M_{2}^3}\mathrm {sin}^{3}i}{M_{1}^2}}.}$

또 다른 ${\displaystyle {극단}_{}}$에서는 M1$M2$({displaystyle M_${1}\ll$ M_${2})$일 때(예를 들어 보이지 않는 물체가 고질량 블랙홀일 때) 질량 함수는^[2]

${\displaystyle f\approx M_{2}\mathrm {sin}^{3}i,}$

0${\displaystyle \sin }$ sin ${\displaystyle (}$ (${\displaystyle i}$ )${\displaystyle 1}$ 1$$1 0 ${\displaystyle {}^{}}$ ${\displaystyle i{90}^{}}$ 90${\displaystyle {}^{}}${\ $1{\displaystyle {\mathrm{}}^{}}$$$for$$ \ $display style$ $0$$${ 0 { 0 { $0$$${ 90 ${\$ {\ \ $leq 90$^ { \ $leq }$$0{\displaystyle \mathrm{}}$ 0 、 mass 함수는 보이지 않는 물체 2의 질량을 하한으로 합니다.^[6]

$일반적$으로 i$\displaystyle$i $또는$ $(\$의 경우

$\displaystyle M_{2}>\mathrm {max} \left(f,f^{1/3}M_{1}^{2/3}\오른쪽).}$

편심 궤도

$편심{\displaystyle }$ 궤도$$e {\$display$ e$\}$에서 질량 함수는 다음과^[7][12] 같습니다.

${{displaystyle f=matrm {M_{2}^{3}\mathrm {orb}{2}^{2}{2}}=matrm {P_{\mathrm {orb}}{2\pi G}}}{-e^2}^{3}/2}.}$

적용들

X선 바이너리

X선 쌍성의 어큐레이터가 톨만-오펜하이머-볼코프 한계(중성자별의 최대 가능한 질량)를 크게 초과하는 최소 질량을 갖는다면 블랙홀이 될 것으로 예상된다.예를 들어 백조자리 X-1의 경우 동반성의 반지름 속도가 ^[13][14]측정되었습니다.

외계 행성

외계행성은 항성-행성계의 질량 중심 주변의 작은 궤도를 따라 움직이게 한다.이 '흔들림'은 별의 반지름 속도가 충분히 높으면 관찰될 수 있습니다.이것은 외계행성을 ^[5][3]탐지하는 지름속도법입니다.질량 함수와 항성 반지름 속도를 이용하여 외계행성의 최소 질량을 결정할 ^{[15][16]: 9 [12][17]}수 있다.이 방법을 태양계에서 가장 가까운 별인 프록시마 센타우리에 적용하면 최소 질량이 1.27인 지상 행성 프록시마 센타우루스 b를 발견할 수 있었다.M를 클릭합니다_Earth.^[18]

펄서 행성

펄서 행성은 펄서 주위를 도는 행성으로 펄서 타이밍을 이용해 여러 개가 발견되었다.펄서의 반경 속도 변화는 ^[4]펄스의 도착 시간 사이의 다양한 간격에 따라 달라집니다.최초의 외계행성은 1992년 밀리초 펄서 PSR 1257+[19]12 주변에서 발견되었다.또 다른 예로는 질량 ^[8]함수에 따르면, PSR J1719-1438 b의 동반자가 목성의 질량과 거의 같은 최소 질량을 갖는 밀리초 펄서 PSR J1719-1438이 있다.

레퍼런스