인자중요 그래프

Factor-critical graph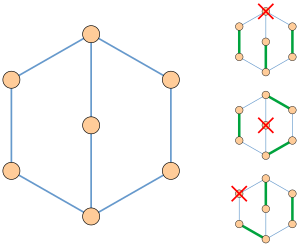
정점 중 하나를 제거하여 형성된 하위 그래프의 완벽한 일치와 함께 요인 중심 그래프.

그래프 이론, 수학적 규율에서 nvertices과에서 n− 1vertices의 모든 부분 그래프. 완벽한 일치하는 있는factor-critical 그래프(또는hypomatchable graph[1][2]) 그래프가 있다. 그것의 가장자리의 속성을 정확히 한개의 하위 집합의 가장자리의 각자가 자신의 vertices의 끝점 화면 그래프에서 완벽한 연결은 하위 집합입니다.)

그래프의 꼭지점 하나를 제외한 모든 것을 포함하는 일치를 거의 완벽한 일치라고 한다.따라서 동등하게, 인자 임계 그래프는 모든 가능한 꼭지점을 피하는 거의 완벽한 일치가 있는 그래프 입니다.

예

해밀턴이 아닌 요인 중심 그래프의 예인 세 가지 우정 그래프
집게가 없는 오각형 피라미드, 발톱이 없는 인자중요 그래프

홀수 길이 사이클 그래프는 정점 수가 홀수인 전체 그래프와 마찬가지로 인자에 중요하다.[1][3]보다 일반적으로 정점 수가 홀수인 해밀턴 그래프는 모두 인자에 중요하다.우정 그래프(단일 공통 꼭지점에서 삼각형 모음을 연결하여 형성된 그래프)는 인자가 중요하지만 해밀턴이 아닌 그래프의 예를 제공한다.

그래프 G가 인자중요하다면 G의 미셀스키안도 마찬가지다.예를 들어, 5V 사이클 그래프의 미셀스키안인 그뢰츠슈 그래프는 인자에 매우 중요하다.[4]

정점 수가 홀수인 2VERx 연결 집게 프리 그래프는 모두 인자에 중요하다.예를 들어, 정규 이코사이드론에서 꼭지점을 제거하여 형성된 11-Vertex 그래프(교량화된 오각형 피라미드의 그래프)는 둘 다 2연결이 되어 있고 발톱이 없어 인자중요하다.이 결과는 정점 수가 짝수인 모든 연결된 집게 없는 그래프가 완벽하게 일치한다는 보다 근본적인 정리로부터 직접적으로 이어진다.[5]

특성화

인자중요 그래프는 각 꼭지점 삭제가 완벽한 일치를 가능하게 하는 그래프로서의 정의가 아닌 여러 가지 다른 방법으로 특성화할 수 있다.

  • Tibor Gallai는 그래프가 연결되어 있고 그래프의 각 노드 v에 대해 v를 포함하지 않는 최대 일치가 존재하는 경우에만 그래프가 인자중요하다는 것을 증명했다.이러한 속성에서 그래프는 홀수 정점 수를 가져야 하며 모든 최대 일치는 하나의 꼭지점을 제외한 모든 정점과 일치해야 한다.[6]
  • Laszlo Lovasz는 그래프가 홀수 귀 분해, 각 가장자리를 일련의 서브그래프로 분할하는 경우에만 인자중요하다는 것을 증명했다. 서브그래프는 홀수 길이 경로 또는 사이클이며, 시퀀스의 첫 번째는 사이클이며, 시퀀스의 각 경로에는 양쪽 끝점이 있지만 이전 서브그래프의 정점에 내부 지점이 없다.hs, 그리고 이전 하위 그래프에서 정확히 하나의 꼭지점을 갖는 시퀀스의 첫 번째가 아닌 각 사이클.예를 들어, 그림의 그래프는 5개의 가장자리와 3개의 가장자리의 경로로 이러한 방식으로 분할될 수 있다.요인 임계 그래프의 거의 완벽한 일치가 주어지는 경우, 각 귀는 일치된 가장자리와 일치하지 않는 가장자리 사이를 교대로 바꾸는 방식으로 귀 분해를 선택할 수 있다.[7][8]
  • 또한 홀수 길이 주기의 연속적인 수축에 의해 단일 꼭지점으로 축소될 수 있는 경우에만 그래프가 인자에 중요하다.더욱이 이 특성화에서는, 이전 사이클의 수축에 의해 형성된 정점을 포함하도록 시퀀스의 각 사이클을 선택할 수 있다.[1]예를 들어, 귀 분해의 귀를 수축할 경우, 분해에 의해 주어진 순서대로 각 귀의 수축 시간에 그것은 홀수 사이클을 형성하므로 귀 분해 특성화는 수축할 일련의 홀수 사이클을 찾는 데 사용될 수 있다.반대로, 각각 이전 수축에서 형성된 정점을 포함하는 일련의 홀수 사이클 수축으로부터, 귀는 각 단계에서 수축된 가장자리의 집합인 귀 분해를 형성할 수 있다.
  • 그래프 G가 정점 v와 v 이외의 모든 정점을 포함하는 일치하는 M 선택과 함께 주어진다고 가정합시다.그 다음 G는 일치된 에지와 일치하지 않는 에지를 교대로 G에 경로 집합이 있는 경우에만 인자중요하다. 이 속성을 바탕으로 주어진 거의 완벽한 일치를 가진 그래프 G가 인자에 중요한지 여부를 선형 시간 내에 결정할 수 있다.[9]

특성.

인자중요 그래프에는 항상 정점의 수가 홀수여야 하며, 2-엣지로 연결되어야 한다(즉, 어떤 브리지도 가질 수 없다).[10]그러나, 그들은 반드시 2-Vertex로 연결되어 있는 것은 아니다. 우정의 그래프는 counterexample을 제공한다.거의 완벽한 일치를 가진 초당적 그래프에서 완벽하게 일치하는 그래프를 만들기 위해 삭제할 수 있는 정점만이 초당적 그래프의 더 큰 쪽에 있는 정점이기 때문에 인자중심의 그래프가 초당적이라는 것은 불가능하다.

m 가장자리가 있는 모든 2Vertex 연결 인자 임계 그래프는 최소 m가 다르고, 보다 일반적으로 m 가장자리와 c 블록(2Vertex 연결 성분)이 있는 모든 인자 임계 그래프는 최소 m - c + 1이 서로 다르고 거의 완벽한 일치를 가진다.이러한 한계가 엄격한 그래프는 특정 형태의 이상한 귀 분해로 특징지어질 수 있다.[3]

연결된 모든 그래프는 충분한 수의 가장자리를 수축하여 인자중요 그래프로 변환될 수 있다.주어진 그래프 G 인자 임계값을 만들기 위해 수축해야 하는 최소 에지 집합은 다항 시간 내에 그래프 인자 임계값을 만들기 위해 수축할 최소 에지 집합을 찾기 위해 탐욕스러운 알고리즘을 사용할 수 있음을 의미한다.[11]

적용들

꽃은 더 큰 그래프의 인자중심의 서브그래프다.꽃은 비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비즈니스 매칭을 위한 잭 에드몬드의 알고리즘에서 핵심적인 역할을 한다.[12]

다면 결합체학에서 인자중요 그래프는 주어진 그래프의 일치하는 폴리토프의 면을 설명하는 데 중요한 역할을 한다.[1][2]

일반화 및 관련 개념

n - k 정점의 모든 부분 집합이 완벽하게 일치하는 경우 그래프는 k-요인-중요하다고 한다.이 정의에서, 하이포매치 가능한 그래프는 1-요인 임계이다.[13]더 일반적으로, n - k 정점의 모든 부분 집합에 r-요인이 있는 경우, 즉 주어진 그래프의 r-정규 하위 그래프의 꼭지점 집합이 그래프인 경우 그래프는 (a,b)-요인-중요인이다.

임계 그래프(정확하지 않음)는 일반적으로 각 정점을 제거하여 그래프 색상에서 필요한 색상 수를 줄이는 그래프를 의미하는 것으로 가정한다.임계도의 개념은 그래프 이론에서 훨씬 더 일반적으로 사용되어 가능한 각 정점을 제거하는 그래프를 참조하거나 그래프의 일부 관련 속성을 변경하지 않는다.일치 임계 그래프는 정점 제거가 최대 일치의 크기를 변경하지 않는 그래프를 의미한다. 갈라이의 특성화에 따르면 일치 임계 그래프는 연결된 모든 구성요소가 인자에 중요한 그래프다.[14]임계 그래프의 보완 그래프는 반드시 일치 중요하며, 이는 갈라이가 임계 그래프의 정점 수에 대한 하한을 증명하기 위해 사용한 사실이다.[15]

그래프 이론을 넘어, 모체에서 귀 분해의 유형을 정의하고, 모든 귀가 홀수인 귀 분해를 갖는 경우 모체 분해를 인자중요로 정의함으로써 인자중요성의 개념을 모체까지 확장시켰다.[16]

참조

  1. ^ a b c d Pulleyblank, W. R.; Edmonds, J. (1974), "Facets of 1-matching polyhedra", in Berge, C.; Ray-Chaudhuri, D. K. (eds.), Hypergraph Seminar, Lecture Notes in Mathematics, vol. 411, Springer-Verlag, pp. 214–242, doi:10.1007/BFb0066196, ISBN 978-3-540-06846-4.
  2. ^ a b Cornuéjols, G.; Pulleyblank, W. R. (1983), "Critical graphs, matchings and tours or a hierarchy of relaxations for the travelling salesman problem", Combinatorica, 3 (1): 35–52, doi:10.1007/BF02579340, MR 0716420.
  3. ^ a b Liu, Yan; Hao, Jianxiu (2002), "The enumeration of near-perfect matchings of factor-critical graphs", Discrete Mathematics, 243 (1–3): 259–266, doi:10.1016/S0012-365X(01)00204-7, MR 1874747.
  4. ^ Došlić, Tomislav (2005), "Mycielskians and matchings", Discussiones Mathematicae Graph Theory, 25 (3): 261–266, doi:10.7151/dmgt.1279, MR 2232992.
  5. ^ Favaron, Odile; Flandrin, Evelyne; Ryjáček, Zdeněk (1997), "Factor-criticality and matching extension in DCT-graphs", Discussiones Mathematicae Graph Theory, 17 (2): 271–278, CiteSeerX 10.1.1.25.6314, doi:10.7151/dmgt.1054, MR 1627955.
  6. ^ 에 의해 인용된 바와 같이Gallai, T. (1963), "Neuer Beweis eines Tutte'schen Satzes", Magyar Tud. Akad. Mat. Kutató Int. Közl., 8: 135–139, MR 0166777.
  7. ^ Lovász, L. (1972), "A note on factor-critical graphs", Studia Sci. Math. Hungar., 7: 279–280, MR 0335371.
  8. ^ Korte, Bernhard H.; Vygen, Jens (2008), "10.4 Ear-Decompositions of Factor-Critical Graphs", Combinatorial Optimization: Theory and Algorithms, Algorithms and Combinatorics, vol. 21 (4th ed.), Springer-Verlag, pp. 235–241, ISBN 978-3-540-71843-7.
  9. ^ Lou, Dingjun; Rao, Dongning (2004), "Characterizing factor critical graphs and an algorithm" (PDF), The Australasian Journal of Combinatorics, 30: 51–56, MR 2080453.
  10. ^ Seyffarth, Karen (1993), "Packings and perfect path double covers of maximal planar graphs", Discrete Mathematics, 117 (1–3): 183–195, doi:10.1016/0012-365X(93)90334-P, MR 1226141.
  11. ^ 시게티, 졸탄(1996년),"한 matroid 그래프 ear-decompositions에 의해 정의되일", Combinatorica, 16(2):233–241, doi:10.1007/BF01844849, MR1401896.한factor-critical 그래프에 도달할(부담이 없는)모서리의 최소 숫자를 축소한 것 1알고리즘의 경우, 프랭크, András(1993년),"그래프의 보수당 편입되지 않고 ear-decompositions", Combinatorica, 13(1):65–81, doi:10.1007/BF01202790, MR1221177를 참조하십시오.
  12. ^ Edmonds, Jack (1965), "Paths, Trees and Flowers", Canadian Journal of Mathematics, 17: 449–467, doi:10.4153/CJM-1965-045-4, MR 0177907.
  13. ^ Favaron, Odile (1996), "On k-factor-critical graphs", Discussiones Mathematicae Graph Theory, 16 (1): 41–51, doi:10.7151/dmgt.1022, MR 1429805.
  14. ^ Erdős, P.; Füredi, Z.; Gould, R. J.; Gunderson, D. S. (1995), "Extremal graphs for intersecting triangles", Journal of Combinatorial Theory, Series B, 64 (1): 89–100, doi:10.1006/jctb.1995.1026, MR 1328293.
  15. ^ 에 의해 인용된 바와 같이Gallai, T. (1963b), "Kritische Graphen II", Publ. Math. Inst. Hungar. Acad. Sci., 8: 373–395.
  16. ^ Szegedy, Balázs; Szegedy, Christian (2006), "Symplectic spaces and ear-decomposition of matroids", Combinatorica, 26 (3): 353–377, doi:10.1007/s00493-006-0020-3, MR 2246153.