결합(추상적 재작성)

컴퓨터 과학에서, 결합은 같은 결과를 내기 위해 어떤 용어들이 한 가지 이상의 방법으로 다시 쓰일 수 있는지를 기술하는, 다시 쓰는 시스템의 속성이다.이 글은 추상적 재작성 시스템의 가장 추상적인 설정에서 속성을 설명한다.

동기부여 사례

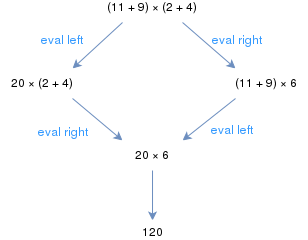
초등 산술의 통상적인 규칙은 추상적인 다시 쓰기 체계를 형성한다.예를 들어, (11 + 9) × (2 + 4)라는 표현은 왼쪽이나 오른쪽 괄호에서 시작하여 평가할 수 있지만, 두 경우 모두 결국 같은 결과를 얻는다.모든 산술 표현이 감산 전략과 무관하게 동일한 결과를 평가하면 산술 재작성 체계는 지반충돌이라고 한다.산술적 재작성 시스템은 재작성 시스템의 세부사항에 따라 결합되거나 지상만 결합될 수 있다.^[1]

두 번째, 보다 추상적인 예는 그 역의 반을 나타내는 각 그룹 원소의 다음과 같은 증거로부터 얻어진다.

그룹 공리

A1	1 ⋅ a	= a
A2	a−1 a	= 1
A3	(a ⋅ b) ⋅ c	= a ⋅ (b ⋅ c)

R4⁻¹ 증명: a⋅(a⋅b) = b

	a−1 ⋅ (a ⋅ b)
=	(a−1 ⋅ a) ⋅ b	A3(r)로
=	1 ⋅ b	A2로
=	b	A1로

R6 증명: (a⁻¹)⁻¹ ⋅ 1 = a

	(a−1)−1 ⋅ 1
=	(a−1)−1 ⋅ (a−1 a a)	A2(r)로
=	a	R4로

R10 증명: (a⁻¹)⁻¹ ⋅ b = ⋅ b

	(a−1)−1 ⋅ b
=	(a−1)−1 ⋅ (a−1 ( ( b))	R4(r)로
=	⋅ b	R4로

R11 증명: ⋅ 1 = a

	⋅ 1
=	(a−1)−1 ⋅ 1	R10(r)로
=	a	R6로

R12 증명: (a⁻¹)⁻¹ = a

	(a−1)−1
=	(a−1)−1 ⋅ 1	R11(r)로
=	a	R6로

이 증명은 주어진 집단의 공리 A1-A3에서 시작하여, 각각의 명제 R4, R6, R10, R11, R12를 몇 개의 초기 명제를 사용하여 5개의 명제 R4, R6, R10, R11, R12를 정립하고, R12가 주 정리인 것이다.일부 증명에는 공리 A2를 역순으로 적용하는 것과 같이 명확하지 않거나 심지어 창의적인 단계가 필요하며, 따라서 R6 증명 첫 단계에서 "1"을⁻¹ "a " a"로 다시 쓰도록 한다.용어 재작성 이론을 발전시킨 역사적 동기 중 하나는 컴퓨터 프로그램은 고사하고 경험 없는 인간에게서는 찾기 어려운 그런 단계의 필요성을 피하려는 것이었다.

용어 재작성 시스템이 합치되고 종료되는 경우, 두 표현식(일명 용어) s와 t: s로 시작하여 가능한 한 왼쪽에서 오른쪽으로 균등하게^{[note 1]} 적용하여 결국 s′라는 용어를 얻는다.t에서 비슷한 방법으로 t′이라는 용어를 구한다.만약 s and와 t′ 두 용어가 문자 그대로 일치한다면, s와 t는 (놀랍지 않게) 동등한 것으로 입증된다.더 중요한 것은, 만약 그들이 동의하지 않는다면, s와 t는 같을 수 없다는 것이다.즉, 동등하게 증명될 수 있는 어떤 두 가지 조건 s와 t도 그 방법에 의해 그렇게 할 수 있다.

결합은 규칙 적용의 모든 순서가 결국 같은 결과로 이어질 것을 보장하므로(종료 속성은 결국 어떤 순서가 종말에 도달하도록 보장함) 그 방법의 성공은 재작성 규칙을 적용하는 특정한 정교한 순서에 의존하지 않는다.따라서, 만약 어떤 동일 이론에 대해 합치되고 종료된 용어 재작성 시스템이 제공될 수 있다면,^{[note 2]} 용어 평등의 증거를 수행하기 위해 창의성의 기미가 필요하지 않다. 따라서 그 작업은 컴퓨터 프로그램에 순응할 수 있게 된다.현대적 접근법은 용어 재작성 시스템보다 더 일반적인 추상적 재작성 시스템을 다루고 있다. 후자는 전자의 특별한 경우다.

일반사례 및 이론

다시 쓰기 시스템은 노드가 표현식을 나타내고 가장자리가 다시 쓰기를 나타내는 방향 그래프로 표현될 수 있다.그래서 예를 들어 a라는 표현이 b로 다시 쓰여질 수 있다면, 우리는 b가 a(대안적으로, a가 b로 줄거나, a가 b의 확장)의 환원이라고 말한다.이것은 화살표 표기법을 사용하여 표현된다. a → b는 a가 b로 감소함을 나타낸다.직관적으로 이것은 해당 그래프가 a에서 b까지의 방향 에지를 가지고 있다는 것을 의미한다.

두 그래프 노드 c와 d 사이에 경로가 있으면 감소 시퀀스를 형성한다.그래서 예를 들면 c → c′ → c′ → c′′ → ...→ d′ → d, 그 다음에 c →→ d를 쓰면 c에서 d로 감소 시퀀스의 존재를 알 수 있다.형식적으로 ∗→는 →의 반사적-변환적 폐쇄다.앞 단락의 예를 들면, 우리는 (11+9)×(2+4)→20×(2+4)→20×(2+4)→20×6이므로 (11+9)××(2+4)→20×6이다.

이것을 확립하면, 결합은 다음과 같이 정의될 수 있다.a pairs S는 모든 쌍 b, c s S에 대해 ∗→b와 ∗→c가 있는 d ∈ S가 존재한다면 합체된 것으로 간주된다(표시 $b{\displaystyle }$ ${\displaystyle \downarrow }$ ${\displaystyle c}$ ${\displaystyle b\mathbin {\downarrow }).$만약 모든 s S가 합체라면 →은 합체라고 말한다.이 성질은 오른쪽에 보이는 도형의 모양을 따서 다이아몬드 성질이라고도 한다.일부 저자들은 도처에 단일 축소가 있는 다이어그램의 변형에 대해 다이아몬드 속성이라는 용어를 유보한다. 즉, a → b, a → c, c, d와 같은 d가 존재해야 한다.단일감소변형은 다중감소변형보다 엄격히 강하다.

지반합성

용어 재작성 시스템은 모든 지상 용어, 즉 변수가 없는 모든 용어가 결합되는 경우 접지 결합된다.^[3]

국부 결합

원소 a ∈ S는 모든 b, c ∈ S에 대해 a → b와 a → c가 존재하는 경우 국소적으로(또는 약하게) 결합된다고 한다.만약 모든 ∈ S가 국부적으로 결합되어 있다면 →은 국부적으로(또는 약하게) 결합체라 불리거나, 약한 Church-Rosser 속성을 가진다.이는 b와 c가 한 번에 a에서 줄여야 한다는 점에서 합종과 다르다.이와 유사하게, 결합은 때때로 전지구적 결합이라고 불린다.

감소 순서에 대한 표기법으로 도입된 관계 ∗→는 그 자체로 재쓰기 시스템으로 볼 수 있는데, 그 관계는 →의 반사적 변환적 종결이다.감소 시퀀스의 순서는 다시 감소 시퀀스(또는 동등하게, 반사-변환성 폐쇄를 형성하는 것이 idempotent이므로), ∗∗→ = ∗→이다.따라서 →→가 국부적으로 합치된 경우에만 → 합치된다.

재작성 시스템은 (광택적으로) 혼합되지 않고 국소적으로 혼합될 수 있다.예는 그림 3과 4에 나와 있다.그러나 뉴먼의 보조정리에서는 국부적 합금재작성 시스템에 무한감소 시퀀스(이 경우 종단 또는 강하게 정상화한다고 한다)가 없다면, 글로벌 합금이라고 기술하고 있다.

처치-로스터 속성

한 선별적 시스템 만일)∗는 y{\displaystyle x{{\stackrel*}{\leftrightarrow}}는 y↔은 Church–Rosser 재산을 소유하고 있는 것}을 뜻한다)↓ y{\displaystyle x{\mathbin{\downarrow}}는 y}모든 개체에, y. 알론조 처치와 존 버클리 로서 1936년에서 람다 계산 이 속성을 가진 사람이고,[5]따라서 증명 t.다고 한다그재산의 이름.^[6] (양다 미적분이 이 재산을 가지고 있다는 사실은 교회-로스터 정리라고도 한다.)Church-Rosser 재산과의 재작성 시스템에서는 단어 문제가 공통의 후계자를 찾는 것으로 축소될 수 있다.Church-Roser 시스템에서, 물체는 적어도 하나의 정상적인 형태를 가지고 있다. 즉, 물체가 존재한다면 그 물체의 정상적인 형태는 독특하지만, 그것은 존재할 수 없다.예를 들어 람다 미적분학에서는 β-축소( sequencex.xx)(λx.xx) → (xx.xx) → (λx.xx) → ...^[7]의 무한 시퀀스가 존재하기 때문에 (λx.xxx)라는 표현은 정상적인 형식이 아니다.

재쓰기 시스템은 합체된 경우에만 Church-Roser 재산을 소유한다.^[8]이러한 동등성 때문에, 정의의 상당부분이 문헌에서 발견된다.예를 들어, "테레즈"에서 Church-Roser 속성과 결합성은 여기에 제시된 결합의 정의와 동의어로 정의되고 동일하다. 여기서 정의한 Church-Roser는 이름을 밝히지 않았지만 동등한 재산으로 주어진다. 다른 본문으로부터의 이러한 이탈은 의도적이다.^[9]

반혼합

단일 재작성 단계에서 주어진 원소에서 도달한 원소만 고려한다는 점에서 국부적 결합의 정의는 전지구적 결합의 정의와 다르다.By considering one element reached in a single step and another element reached by an arbitrary sequence, we arrive at the intermediate concept of semi-confluence: a ∈ S is said to be semi-confluent if for all b, c ∈ S with a → b and a ∗→ c there exists d ∈ S with b ∗→ d and c ∗→ d; if every a ∈ S is semi-confluent, we say that → is semi-confluent.

반혼합 원소는 결합할 필요가 없지만, 반혼합 재쓰기 시스템은 반드시 결합하며, 결합체계는 하찮은 반혼합이다.

강한 결합

강한 결합은 지역 결합에 대한 또 다른 변화로, 재작성 시스템이 전세계적으로 결합되어 있다고 결론을 내릴 수 있게 해준다.원소 a ∈ S는 모든 b, c ∈ S에 대해 b ∗→d와 c → d가 존재하는 경우 강하게 결합한다고 하며, ; S가 강하게 결합되는 경우 → 는 강하게 결합한다고 한다.

결합 원소는 강하게 결합될 필요는 없지만, 강력한 결합 재쓰기 시스템은 반드시 결합된다.

혼합 시스템의 예

• 다항식 모듈로의 축소는 그뢰브너 기반으로 작업할 경우 합체된 재작성 시스템이다.
• 마쓰모토의 정리는 땋은 관계가 합쳐진 데서 비롯된다.
• β-절단계의 감소는 Church-Roser 정리에 의해 결합된다.

참고 항목

• 수렴(로직)
• 임계 쌍(로직)
• 일반 양식(추상 재작성)

메모들

참조

• 2003년 이론 컴퓨터 과학의 케임브리지 Tracts, Terse, 용어 다시 쓰기 시스템.
• 용어 다시 쓰기와 모든 것, 프란츠 바더와 토바이어스 닙코우, 캠브리지 대학 출판부, 1998년

외부 링크

• Weisstein, Eric W. "Confluent". MathWorld.