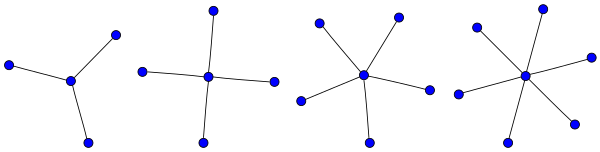
별(그래프 이론)

Star (graph theory)
별
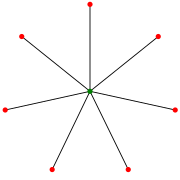Star network 7.svg
별7 S(일부 저자는 이를 S로8 색인화합니다.)
꼭지점k + 1
가장자리k
직경2
둘레∞
색수2
색채 지수k
특성.엣지-트랜시
트리
단위 거리
초당파
표기법Sk
그래프 및 매개 변수 표

그래프 이론에서 별k S는 완전한 이분 그래프1,k K: 하나의 내부 노드가 있고 k가 남는다(그러나 내부 노드가 없고 k가 1일 때 k + 1이 남는다).또는 일부 저자는 S를 최대 직경 2의 k순서로 정의한다k. 이 경우 k > 2의 별은 k - 1의 잎을 가진다.

가장자리가 세 개인 별은 발톱이라고 불립니다.

별k S는 k가 홀수일 때가 아니라 짝수일 때 가장자리를 장식한다.엣지 전이성냥개비 그래프로 지름 2(l > 1일 때), 둘레 θ(주기 없음), 색지수 k 및 색수 2(k > 0일 때)를 가진다.또한 이 별은 큰 자기동형성군, 즉 k자 위의 대칭군을 가지고 있다.

별은 또한 최대 하나의 정점이 하나보다 큰 도를 갖는 유일한 연결된 그래프로 설명될 수 있습니다.

다른 그래프 패밀리와의 관계

발톱은 발톱이 없는 그래프의 정의에서 주목할 만한 것으로, 유도 하위 [1][2]그래프로 손톱이 없는 그래프이다.이들은 또한 휘트니 그래프 동형 정리의 예외적인 경우 중 하나이다: 일반적으로, 동형 선 그래프를 가진 그래프는 발톱과 삼각형3 [3]K를 제외하고 그 자체로 동형이다.

별은 특별한 종류의 나무입니다.다른 나무와 마찬가지로 별은 프뤼퍼 수열로 부호화될 수 있다. 별1,k K의 프뤼퍼 수열은 중심 [4]정점의 k - 1 복사본으로 구성된다.

몇 가지 그래프 불변량은 별의 관점에서 정의된다.숲의 스타 arboricity은 최소 수 이것을 그래프 등으로 각 숲에서 각 나무는 star,[5] 색상과 그러한 방법으로 매일 2가지 컬러 수업 함께 모든 연결된 구성 요소들은 별들은 부분 그래프를 형성한 그것의 vertices에 색을 필요한 그래프의 별 색 수가 최소 수 분리할 수 있다.[6]분기 폭 1의 그래프는 연결된 각 성분이 별인 [7]그래프입니다.

별 그래프는34 S, S5, S 및6 S입니다.

기타 응용 프로그램

발톱의 꼭지점 사이의 거리 집합은 어떤 차원의 [8]유클리드 공간에 등각적으로 삽입될 수 없는 유한 미터법의 한 예를 제공한다.

스타 네트워크는 스타 그래프를 본뜬 컴퓨터 네트워크로서 분산 컴퓨팅에서 중요합니다.

일정한 길이의 간격을 가진 가장자리를 식별함으로써 형성되는 스타그래프의 기하학적 실현을 열대기하학에서의 곡선의 국소모델로 사용한다.열대곡선은 별 모양 메트릭 그래프와 국소적으로 동형인 메트릭 공간으로 정의된다.

레퍼런스

Wikimedia Commons에는 별 그래프와 관련된 미디어가 있습니다.
  1. ^ 를 클릭합니다Faudree, Ralph; Flandrin, Evelyne; Ryjáček, Zdeněk (1997), "Claw-free graphs — A survey", Discrete Mathematics, 164 (1–3): 87–147, doi:10.1016/S0012-365X(96)00045-3, MR 1432221.
  2. ^ 를 클릭합니다Chudnovsky, Maria; Seymour, Paul (2005), "The structure of claw-free graphs", Surveys in combinatorics 2005 (PDF), London Math. Soc. Lecture Note Ser., vol. 327, Cambridge: Cambridge Univ. Press, pp. 153–171, MR 2187738.
  3. ^ 를 클릭합니다Whitney, Hassler (January 1932), "Congruent Graphs and the Connectivity of Graphs", American Journal of Mathematics, 54 (1): 150–168, doi:10.2307/2371086, hdl:10338.dmlcz/101067, JSTOR 2371086.
  4. ^ Gottlieb, J.; Julstrom, B. A.; Rothlauf, F.; Raidl, G. R. (2001). "Prüfer numbers: A poor representation of spanning trees for evolutionary search" (PDF). GECCO-2001: Proceedings of the Genetic and Evolutionary Computation Conference. Morgan Kaufmann. pp. 343–350. ISBN 1558607749.
  5. ^ Hakimi, S. L.; Mitchem, J.; Schmeichel, E. E. (1996), "Star arboricity of graphs", Discrete Math., 149: 93–98, doi:10.1016/0012-365X(94)00313-8
  6. ^ 를 클릭합니다Fertin, Guillaume; Raspaud, André; Reed, Bruce (2004), "Star coloring of graphs", Journal of Graph Theory, 47 (3): 163–182, doi:10.1002/jgt.20029.
  7. ^ 를 클릭합니다Robertson, Neil; Seymour, Paul D. (1991), "Graph minors. X. Obstructions to tree-decomposition", Journal of Combinatorial Theory, 52 (2): 153–190, doi:10.1016/0095-8956(91)90061-N.
  8. ^ Linial, Nathan (2002), "Finite metric spaces–combinatorics, geometry and algorithms", Proc. International Congress of Mathematicians, Beijing, vol. 3, pp. 573–586, arXiv:math/0304466, Bibcode:2003math......4466L