전체 양당 그래프

전체 양당 그래프
m = 5 및 n = 3인 완전한 초당적 그래프
정점	n + m
가장자리	mn
반지름	${\displaystyle \left\{\\put{array}{ll}1&m=1\vee n=1\\2\{\text{data}}\end{array}}\right.}$
지름	${\displaystyle \left\{\\put{array}{ll}1&m=n=1\\\2&{\text{data}}\end{array}}\right.}$
둘레	${\displaystyle \left\{\nft{array}{ll}\inflt &m=1\lor n=1\\\lor n=1\\\n4&{\text}}\end{array}}\right.}$
자동형성	${\displaystyle \left\{\put{narray}{ll}2m!n!&n=m\\m!n!&{\text{data}\end{array}\오른쪽.}$
색수	2
색도 지수	max{m, n}
스펙트럼	${\displaystyle \왼쪽\{0^{n+m-2}(\pm {\sqrt {nm})^{1}\오른쪽\}}}$
표기법	${\displaystyle K_{m,n}}$
그래프 및 모수 표

그래프 이론의 수학적 분야에서 완전한 초당적 그래프나 바이클릭은 첫 번째 세트의 모든 꼭지점이 두 번째 세트의 모든 꼭지점에 연결되는 특별한 종류의 초당적 그래프다.^[1][2]

그래프 이론 자체는 일반적으로 레온하르트 오일러의 쾨니히스베르크의 7대교에 관한 1736년 저술에서 시작된 것으로 연대를 한다.그러나, 아타나시우스 커처가 편집한 라몬 렐의 작품 판과 관련하여, 이미 1669년경 완전한 초당적 그래프의 도면이 인쇄되었다.^[3][4]렐 자신도 3세기 전에 완성된 그래프의 유사한 그림을 그렸었다.^[3]

정의

완전한 초당적 그래프는 정점을 두 하위 집합 V와₁ V로₂ 분할할 수 있는 그래프로, 어떤 에지도 동일한 하위 집합에 두 끝점을 가지지 않고 다른 하위 집합에서 정점을 연결할 수 있는 모든 가능한 에지가 그래프의 일부분이다.즉, v graph V와₁₁ v₂ ∈ V의₂₂ 두 꼭지점마다 vv가₁₂ E의 에지라고 하는 양립자 그래프(V₁, V, E)이다.크기 V₁ = m, V = n의₂ 분할이 있는 완전한 초당적 그래프는 K로_m,n 표시된다.^[1][2] 동일한 기호를 가진 두 개의 그래프는 모두 이형이다.

예

• 어떤 k에 대해서도 K는_1,k 별이라고 불린다.^[2]나무인 완전한 초당적 그래프는 모두 별이다.
  • 그래프 K는_1,3 집게라고 불리며 집게 없는 그래프를 정의하는 데 사용된다.^[5]
• 그래프_3,3 K를 효용 그래프라고 한다.이 용도는 3개의 건물에 각각 3개의 유틸리티를 연결해야 하는 표준 수학 퍼즐에서 나온 것으로, K의_3,3 비구명성으로 인해 교차하지 않으면 풀 수 없다.^[6]
• 관계의 디그그래프에서 서브그래프로 발견된 최대 바이크리를 개념이라고 한다.이러한 하위 그래프를 만나 결합함으로써 격자가 형성되는 경우, 관계에는 유도 개념 격자가 있다.이러한 형태의 관계 분석을 형식 개념 분석이라고 한다.

특성.

예제_p,p K 완전한 초당적 그래프^[7]

K3,3	K4,4	K5,5
엣지 컬러링 3가지	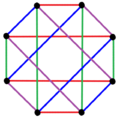네 가지 엣지 컬러링	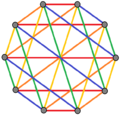엣지컬러 5가지
형식 2{4}p의 일반 복합 폴리곤에는 2p 정점(빨간색 및 파란색)과2 p 2-에지(edge)가 있는 완전한 쌍방향 그래프가 있다.그것들은 또한 p 엣지 컬러링으로도 그려질 수 있다.

• 초당적 그래프가 주어진 경우 매개변수 i에 대해 완전한 초당적 하위 그래프 K를_i,i 포함하는지 여부를 테스트하는 것은 NP-완전한 문제다.^[8]
• 평면 그래프는 K를_3,3 마이너로 포함할 수 없으며, 외부 평면 그래프는 K를_3,2 마이너로 포함할 수 없다(이러한 조건들은 평면성과 외부 평면성에 충분하지 않지만 필요함).반대로 모든 비계획 그래프에는 K 또는_3,3 전체 그래프 K가₅ 마이너로서 포함되어 있다. 이것이 바그너의 정리다.^[9]
• 모든 완전한 초당적 그래프.K는_n,n 무어 그래프와 a (n,4)-cage이다.^[10]
• 완전한 양분 그래프 K와_n,n K는_n,n+1 정점 수가 같은 삼각형이 없는 모든 그래프 중에서 가능한 최대 에지 수를 가지고 있다. 이것이 맨텔의 정리다.맨텔의 결과는 투란의 정리에서 서브그래프로서 더 큰 부조화를 피하는 k-partite 그래프와 그래프로 일반화되었고, 이 두 가지 완전한 쌍방향 그래프는 투란 그래프의 예로서, 이 보다 일반적인 문제에 대한 극단적 그래프인 투란 그래프의 예들이다.^[11]
• 전체 초당적 그래프 K는_m,n 최소{m, n}의 정점을 포함하며 최대{m, n}의 숫자를 포함하는 가장자리가 있다.
• 전체 초당적 그래프 K에는_m,n 최대 크기{m, n}의 최대 독립 집합이 있다.
• 완전 양분 그래프 K의_m,n 인접 행렬은 고유값이 √nm, -√nm,^[12] 0이며, 각각 다중성 1, 1 및 n+m-2이다.
• 완전한 초당적 그래프 K의_m,n 라플라시안 행렬은 고유값 n+m, n, m, 0을 가지며, 각각 다중성 1, m-1, n-1, 1을 가진다.
• 완전한 초당적 그래프 K에는_m,n mⁿ⁻¹ n 스패닝^m−1 트리가 있다.^[13]
• 완전한 초당적 그래프 K는_m,n 최소 크기{m,n}의 최대 일치를 가진다.
• 완전한 초당적 그래프 K는_n,n 라틴 사각형에 해당하는 적절한 n-엣지 색상을 가지고 있다.^[14]
• 모든 완전한 초당적 그래프는 모듈형 그래프다. 모든 정점의 세 쌍은 정점의 각 쌍 사이의 최단 경로에 속하는 중위수를 가지고 있다.^[15]

참고 항목

• Biclique-free 그래프(Biclique-free graph)는 완전한 초당적 하위 그래프를 회피하여 정의된 희소성 그래프의 일종이다.
• 크라운 그래프, 완전한 초당적 그래프에서 완벽한 일치를 제거하여 형성된 그래프
• 전체 다중 사이트 그래프, 전체 쌍방향 그래프를 세 개 이상의 정점 집합으로 일반화
• 비클릭 공격

참조