클로징 네트워크

통신 분야에서 Clos 네트워크는 실용적이고 다단계적인 스위칭 시스템의 이론적 이상화를 나타내는 다단계 회로 스위칭 네트워크의 일종이다. 1938년 에드슨 어윈에^[1] 의해 발명되었고, 1952년 찰스 클로스(프랑스어 발음: [ʃaʁl klo])^[2]에 의해 처음으로 공식화되었다.

스테이지를 추가함으로써 클로징 네트워크는 대형 크로스바 스위치를 구성하는 데 필요한 크로스포인트 수를 줄인다. 클로징 네트워크 토폴로지(아래 다이어그램)는 세 개의 정수 n, m 및 r에 의해 매개변수로 지정된다. n은 각 수신 단계 크로스바 스위치에 공급되는 소스 수를 나타낸다. 각 수신 단계 크로스바 스위치에는 m 출구가 있고, m 중간 단계 크로스바 스위치가 있다.

회로 스위칭은 연결 기간 동안 엔드포인트 사이의 연결을 위한 전용 통신 경로를 정렬한다. 이것은 전용 연결이 잘 활용되지 않는 경우 이용 가능한 총 대역폭을 희생시키지만, 연결과 대역폭을 더 예측 가능하게 만들고, 현대의 패킷 교환 네트워크에서처럼 취급되는 모든 패킷이 아닌, 연결이 시작될 때에만 제어 오버헤드를 도입한다.

Clos 네트워크가 처음 고안되었을 때, 교차점 수는 스위칭 시스템의 총 비용에 대한 좋은 근사치였다. 이는 전기기계적 크로스바에 중요했지만, 실리콘에서 직접 또는 상대적으로 작은 보드 클러스터 내에서 상호연결이 구현될 수 있는 VLSI의 출현과 덜 관련이 있게 되었다. 각각 광섬유 링크를 기반으로 하는 거대한 상호 연결 구조를 가진 복잡한 데이터 센터가 등장하자 클로즈 네트워크는 다시 중요해졌다.^[3] 클로즈 네트워크의 하위 유형인 베네시 네트워크도 최근 머신러닝에서 응용 분야를 발견했다.^[4]

위상

클로징 네트워크는 수신 단계, 중간 단계, 송신 단계 등 3단계로 구분된다. 각 단계는 여러 개의 크로스바 스위치(아래 다이어그램 참조), 흔히 크로스바라고 부른다. 네트워크는 단계들 사이에 완전한 r-way를 구현한다. 수신 크로스바 스위치로 들어오는 각 통화는 사용 가능한 중간 단계 크로스바 스위치를 통해 관련 송신 크로스바 스위치로 라우팅될 수 있다. 수신 스위치를 중간 단계 스위치에 연결하는 링크와 중간 단계 스위치를 송신 스위치에 연결하는 링크가 모두 무료인 경우, 특정 새 호출에 중간 단계 크로스바를 사용할 수 있다.

클로징 네트워크는 세 개의 정수로 정의되며, n, m 및 r. n은 각 r 수신 단계 크로스바 스위치에 공급되는 소스 수를 나타낸다. 각 수신 단계 크로스바 스위치에는 m 출구가 있고, m 중간 단계 크로스바 스위치가 있다. 각 수신 단계 스위치와 각 중간 단계 스위치 사이에는 정확히 하나의 연결이 있다. 각각 m 입력과 n 출력을 가진 송신 단계 스위치가 있다. 각 중간 단계 스위치는 각 대피 단계 스위치에 정확히 한 번 연결된다. 따라서 수신 단계에는 r 스위치가 있으며, 각 스위치에는 n개의 입력과 m 출력이 있다. 중간 단계에는 m 스위치가 있으며, 각 스위치에는 r 입력과 r 출력이 있다. 송신 단계에는 r 스위치가 있으며, 각 스위치에는 m 입력과 n 출력이 있다.

차단특성

m과 n의 상대적 값은 Closing 네트워크의 차단 특성을 정의한다.

엄격한 감지 비차단 Closing 네트워크 (m 2 2n-1): 원래 1953 Closing 결과

m ≥ 2n-1인 경우, Closing 네트워크는 엄격한 감지 비차단이므로, 수신 스위치의 미사용 입력을 기존 호출을 재조정할 필요 없이 항상 송신 스위치의 미사용 출력에 연결할 수 있다. 이것은 Clos의 고전적인 1953년 논문의 기초를 형성한 결과물이다. 수신 스위치의 입력에 자유 단자가 있다고 가정하고, 이 단자는 특정 송신 스위치의 자유 단자에 연결되어야 한다. 최악의 경우, n-1 다른 호출은 해당 수신 스위치에서 활성화되며, n-1 다른 호출은 해당 송신 스위치에서 활성화된다. 또한 최악의 경우, 이러한 각각의 통화는 다른 중간 단계 스위치를 통과한다고 가정한다. 따라서 최악의 경우, 중간 단계 스위치의 2n-2는 새로운 통화를 전달할 수 없다. 따라서 엄격한 감지 비차단 작동을 위해 또 다른 중간단계 스위치가 필요하여 총 2n-1이 된다.

Closing nonblocking Closing networks(m ≥ n)

m ≥ n이면, Clos 네트워크는 차단할 수 없는 상태여서, 수신 스위치의 미사용 입력을 송신 스위치의 미사용 출력에 항상 연결할 수 있지만, 이를 위해서는 Clos 네트워크의 다른 중앙 단계 스위치에 할당하여 기존 통화를 재정렬해야 할 수 있다.^[5] 이를 증명하기 위해, Clos 네트워크가 충분히 활용되고 있는 m = n, 즉 r×n 호출을 고려하는 것으로 충분하다. 증거는 이러한 r×n 입력 단자가 r×n 출력 단자에 대한 순열은 어떻게 더 작은 순열로 분해될 수 있는지 보여주며, 각 순열은 m = n으로 Closing 네트워크의 개별 크로스바 스위치에 의해 구현될 수 있다.

그 증거는 홀의 결혼 정리를 사용하는데^[6], 이 이름은 종종 다음과 같이 설명되기 때문에 이 이름이 주어진다. 남자아이와 여자아이가 있다고 가정해 보자. 정리는 그들 사이에 있는 k 소년들의 모든 부분 집합(0 ≤ k r r)이 k 또는 그 이상의 소녀를 알고 있다면, 각 소년들은 그가 알고 있는 소녀와 짝지어질 수 있다고 기술하고 있다. 이것이 짝짓기가 일어나기 위해 꼭 필요한 조건이라는 것은 명백하다; 놀라운 것은 그것이 충분하다는 것이다.

클로즈 네트워크의 맥락에서, 각각의 소년은 수신 스위치를 나타내고, 각각의 소녀는 송신 스위치를 나타낸다. 남학생은 해당 수신 및 송신 스위치가 동일한 전화를 걸면 여학생을 안다고 한다. k 수신 스위치는 k×n 호출을 전달하며, 이러한 통화는 송신 스위치보다 작은 스위치로는 운반할 수 없기 때문에 각 k 소년 세트는 적어도 k 소녀를 알아야 한다. 따라서 각 수신 스위치는 일대일 매핑을 통해 동일한 호출을 전달하는 송신 스위치와 페어링할 수 있다. 이러한 r 통화는 한 개의 중간 단계 스위치로 수행할 수 있다. 만약 이 중간 단계 스위치가 이제 Clos 네트워크에서 제거된다면, m은 1 감소하고, 우리는 더 작은 Clos 네트워크가 남게 된다. 그 과정은 m = 1까지 반복되며, 모든 통화는 중간 단계 스위치에 할당된다.

블럭화 확률: Lee 및 Jacobaeus 근사치

실제 전화 교환 시스템은 비용상의 이유로 엄격한 의미의 비차단 시스템이 거의 없으며, 차단할 확률은 적으며, 이는 리나 자코바이에우스 근사치로 평가될 수 있는 것으로,^[7] 기존 통화의 재배치가 없다고 가정한다. 여기서 각 수신 또는 송신 스위치에 대한 기타 활성 통화의 잠재적 수는 u = n-1이다.

리 근사치에서 스테이지 사이의 각 내부 링크는 이미 일정한 확률 p를 가진 호출에 의해 점유되고 있으며, 이는 서로 다른 링크들 사이에서 완전히 독립적이라고 가정한다. 이는 특히 작은 r에 대한 블럭화 확률을 과대평가한다. 주어진 내부 링크가 사용 중일 확률은 p = uq/m이며, 여기서 q는 수신 또는 송신 링크가 사용 중일 확률이다. 반대로 링크가 자유일 확률은 1-p이다. 특정 중간 단계 스위치를 통해 송신 스위치에 수신 스위치를 연결하는 경로가 자유일 확률은 두 링크 모두 자유일 확률(1-p)이다.² 따라서 사용할 수 없을 확률은 1-(1-p)² = 2p-p이다². 차단의 확률 또는 그러한 경로가 자유롭지 않을 확률은 [1-(1-p)]^2m이다.

Jacobaeus 근사치는 더 정확하며, 어떻게 도출되는지 보기 위해 Clos 네트워크에 들어가는 통화의 특정 매핑(입력 통화)이 이미 중간 단계 스위치에 존재한다고 가정한다. 이는 수신 스위치와 송신 스위치의 상대적 구성만 관련이 있다는 사실을 반영한다. 연결할 자유 입력 단자와 동일한 수신 스위치를 통해 들어오는 i 입력 호출이 있고, 연결할 자유 출력 단자와 동일한 송신 스위치를 통해 클로징 네트워크(출력 호출)를 나가는 j 호출이 있다. 따라서 0 ≤ i ≤ u, 0 ≤ j u u.

A를 m 중간 단계 스위치에 j 출력 호출을 할당하는 방법의 개수로 한다. B를 차단을 초래하는 이러한 과제의 수가 되게 하라. 이는 나머지 m-j 중간 단계 스위치가 i 입력 호출의 m-j와 일치하는 경우의 수로서, 이 통화의 m-j를 포함하는 하위 집합의 수입니다. 블럭화 확률은 다음과 같다.

${\displaystyle \beta _{ij}={\frac {B}{A}}={\frac{\frac({\begin{array}{c}i\\\m-j\end{array}\rigin}{c}m\j\end}\rigin}\rigin}\rigin}\right)}}{\begin}}}}}={\frac {i!j!}{{(i+j-m)!m!}}$

f가_i i 다른 호출이 수신 스위치에서 이미 활성 상태일 확률이고 g가_j 다른 호출이 송신 스위치에서 이미 활성 상태일 확률이라면, 전체적인 차단 확률은 다음과 같다.

${\displaystyle P_{B}=\sum _{i=0}^{u}\sum _{j=0}^{j}f_{i}g_{j}\beta _{ij}}}}}}}}}}}}$

이는 이항 분포로 각각 나타내는 f와_i g로_j 평가할 수 있다. 상당한 대수학적 조작 후, 이것은 다음과 같이 쓰여질 수 있다.

${\displaystyle P_{B}={\frac {(u!)^{2}(2-p)^{2u-m}p^{m}{m!(2u-m)!}}}$

3단계 이상의 네트워크 폐쇄

폐쇄 네트워크는 또한 홀수 수의 단계로 일반화될 수 있다. 각 중앙 단계 크로스바 스위치를 3단계 클로징 네트워크로 교체하여 5단계 클로징 네트워크를 구축할 수 있다. 같은 과정을 반복적으로 적용함으로써 7, 9, 11, ...단계가 가능하다.

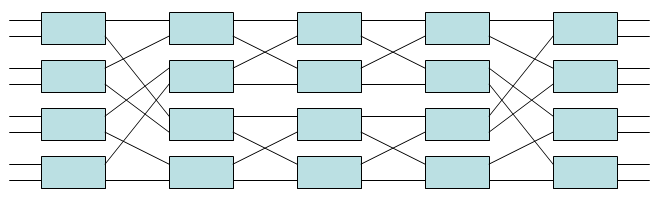
베네시 네트워크(m = n = 2)

m = n = 2를 갖는 이러한 유형의 비차단 네트워크는 Vaclav E 이전의 다른 사람들에 의해 논의되고 분석되었음에도 불구하고 일반적으로 베네시 네트워크라고 불린다. 베네시. 입력과 출력 수는 N = r×n = 2r이다. 이러한 네트워크는 각각 N/2 2×2 크로스바 스위치를 포함하는 2개의 logN₂ - 1단계를 가지며, 총 N logN₂ - N/2 2×2 크로스바 스위치를 사용한다. 예를 들어, 8×8 베네시 네트워크(예: N = 8)는 아래와 같다. 각 단계는 N/2 = 4 2×2 크로스바 스위치를 포함하는 2개의 log8₂ - 1 = 5단계를 가지며, 총 N logN₂ - N/2 = 20 2×2 크로스바 스위치를 사용한다. 중앙 3단계는 두 개의 작은 4×4 베네시 네트워크로 구성되지만, 중앙 단계에서는 각각의 2×2 크로스바 스위치 자체가 2×2 베네시 네트워크로 간주될 수 있다. 따라서 이 예는 이러한 유형의 네트워크의 재귀적 구성을 강조한다.

참고 항목

• 네트워크를 연결하는 대안적인 방법인 Banyan 스위치
• 네트워크를 연결하는 대안적인 방법인 Fat Tree
• 네트워크를 연결하는 대안적인 방법인 오메가 네트워크

참조