센서 평면의 좌표(2차원)를 물체 좌표(3차원)와 연관시키기 위해 광도측정 및 컴퓨터 스테레오 시야에 사용되는 2개의 방정식 세트
공선도 방정식은 광도 측정과 컴퓨터 스테레오 시야에 사용되는 두 방정식의 집합으로, 센서 평면의 좌표(2차원)를 물체 좌표(3차원)와 연관시킨다. 방정식은 카메라의 광학 중심을 통해 물체의 한 지점을 센서 평면의 이미지로 중앙 투영하는 것에서 비롯된다.[1]

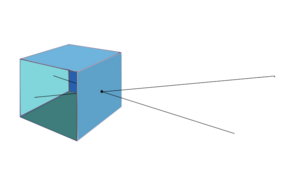
P, Q, R 세 점은 투영 중심 C를 통해 평면 S에 투영된다. 정의
x,y 및 z는 센서 평면에서 x축과 y축이 있는 좌표계를 참조한다. Denote the coordinates of the point P on the object by  , the coordinates of the image point of P on the sensor plane by x and y and the coordinates of the projection (optical) centre by
, the coordinates of the image point of P on the sensor plane by x and y and the coordinates of the projection (optical) centre by  . As a consequence of the projection method there is the same fixed ratio
. As a consequence of the projection method there is the same fixed ratio  between
between  and
and  ,
,  and
and  , and the distance of the projection centre to the sensor 평면 z = 및
, and the distance of the projection centre to the sensor 평면 z = 및  - z
- z  따라서 다음과 같다.
따라서 다음과 같다.



마지막 방정식에서 을(를) 해결하고 다른 방정식에 입력하면 다음과 같은 결과가 나온다.
을(를) 해결하고 다른 방정식에 입력하면 다음과 같은 결과가 나온다.


P 지점은 일반적으로 좌표 X, Y, Z에 의해 카메라 "외부"에 표시되며 투영 중심은  이러한 좌표는 카메라의 시스템에 대한 회전과 번역을 통해 변환될 수 있다. 번역은 좌표의 차이에 영향을 미치지 않으며, 카메라 변환이라고 불리는 회전은 3×3 매트릭스 R에 의해 주어지며, 변환- X Y- - - Z ) (0},Y_을
이러한 좌표는 카메라의 시스템에 대한 회전과 번역을 통해 변환될 수 있다. 번역은 좌표의 차이에 영향을 미치지 않으며, 카메라 변환이라고 불리는 회전은 3×3 매트릭스 R에 의해 주어지며, 변환- X Y- - - Z ) (0},Y_을 다음과 같이 한다.
다음과 같이 한다.


그리고

이러한 식을 대체하면 공선성 방정식이라고 알려진 두 개의 방정식을 얻게 된다.


이러한 방정식의 가장 분명한 용도는 카메라에 의해 기록된 영상에 대한 것이다. 이 경우 방정식은 객체 공간(X, Y, Z)에서 영상 좌표(x, y)로의 변환을 설명한다. 그것은 번들 조정에서 사용되는 방정식의 기초를 형성한다. 그들은 사진을 찍을 때 이미지 포인트(카메라의 센서 플레이트 위), 관찰 포인트(물체 위) 및 카메라의 투영 중심이 정렬되었음을 나타낸다.
참고 항목
참조

















 다음과 같이 한다.
다음과 같이 한다. 






