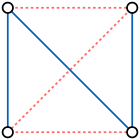
보완 그래프
Complement graph
그래프 이론에서 그래프 G의 보완점 또는 역점은 동일한 정점에 있는 그래프 H로, G에 인접하지 않은 경우에만 H의 두 개의 뚜렷한 정점이 인접해 있다.즉, 그래프의 보완을 생성하기 위해 완전한 그래프를 형성하는 데 필요한 모든 결측 가장자리를 채우고 이전에 있던 가장자리를 모두 제거한다.[1]
보어는 그래프의 설정된 보수가 아니며, 가장자리만 보완된다.
정의
G = (V, E)를 단순 그래프로 하고 K를 V의 모든 2-element 하위 집합으로 구성한다.그 다음 H = (V, K \ E)는 G의 보완물이고,[2] 여기서 K \ E는 K의 E의 상대적 보완물이다.지시된 그래프의 경우, 위의 공식에서 설정된 K 대신에 모든 2-element 쌍의 V를 사용하여 동일한 정점 집합에 대한 지시된 그래프와 같은 방식으로 보완을 정의할 수 있다.그래프의 인접 행렬 A에 있어 Q가 정점 수가 같은 전체 그래프의 인접 행렬(즉, 대각선 입력이 0인 것을 제외한 모든 항목은 통일)인 경우, A의 보완 행렬은 Q-A이다.
다중 글씨에 대한 보완책이 정의되어 있지 않다.자가 루프를 허용하는 그래프에서(다중 보조성은 아니지만) G의 보완성은 G에 없는 모든 정점에 자가 루프를 추가하고, 그렇지 않으면 위와 같은 공식을 사용하여 정의할 수 있다.그러나 이 연산은 단순 그래프의 경우와는 다른데, 자기 루프가 없는 그래프에 적용하면 모든 정점에 자기 루프가 있는 그래프가 생성되기 때문이다.
응용 프로그램 및 예제
몇 가지 그래프 이론적 개념은 보완을 통해 서로 관련된다.
- 엣지 없는 그래프의 보완은 완전한 그래프와 그 반대다.
- 그래프 G의 보완 그래프의 유도 하위 그래프는 G의 해당 유도 하위 그래프의 보완이다.
- 그래프의 독립 집합은 보완 그래프의 클라이크이며 그 반대의 경우도 마찬가지다.독립 집합은 엣지리스 유도 서브그래프, 클라이크는 완전 유도 서브그래프인 만큼 이전 두 특성의 특수한 경우다.
- 그래프의 자동형 집단은 그 보완물의 자동형 집단을 말한다.
- 모든 삼각형이 없는 그래프의 보완점은 비록 그 반대는 사실이 아니지만,[3] 발톱이 없는 그래프다.
자가 완성 그래프 및 그래프 클래스
자기 보완 그래프는 그 자체의 보완에 대해 이형화된 그래프다.[1]예로는 4Vertex 경로 그래프와 5Vertex 주기 그래프가 있다.자기 완성 그래프의 알려진 특성화는 없다.
이러한 클래스 중 하나에 있는 그래프의 보완이 동일한 클래스의 다른 그래프라는 점에서 여러 클래스의 그래프는 자체 보완적이다.
- 완벽한 그래프는 모든 유도 하위 그래프에 대해 색도 수가 최대 클라이크의 크기와 같은 그래프다.완벽한 그래프의 보완도 완벽하다는 사실은 라슬로 로바스츠의 완벽한 그래프 정리다.[4]
- Cographs는 분리 결합과 보완 연산에 의해 단일 정점으로부터 구축될 수 있는 그래프로 정의된다.그들은 자기 완성형 그래프 집단을 형성한다: 모든 cograph의 보완은 또 다른 cograph이다.두 개 이상의 정점 이상의 cograph의 경우, 각 보완 쌍에서 정확히 하나의 그래프가 연결되며, cograph의 동일한 정의는 각각의 연결된 유도 하위그래프마다 분리된 보완이 있다는 것이다.또 다른 자체 보완적 정의는 4Vertex 경로의 형태로 유도 하위 그래프가 없는 그래프라는 것이다.[5]
- 그래프의 또 다른 자기 완성 등급은 분할 그래프의 등급으로, 정점을 패거리와 독립 집합으로 분할할 수 있는 그래프다.같은 칸막이가 보완 그래프에서 독립된 집합과 클라이크를 제공한다.[6]
- 임계값 그래프는 독립 정점(이웃이 없는 정점) 또는 범용 정점(이전에 추가된 모든 정점에 인접)을 반복적으로 추가함으로써 형성된 그래프다.이 두 연산은 상호 보완적이며 자체 완성 등급의 그래프를 생성한다.[7]
알고리즘 측면
그래프의 알고리즘 분석에서 그래프와 그 보어의 구별은 중요한데, 그 이유는 스파스 그래프(정점 쌍의 수에 비해 가장자리 수가 적은 그래프)는 일반적으로 희소 보완을 가지지 않기 때문에, 주어진 그래프에 있는 가장자리 수에 비례하여 시간이 걸리는 알고리즘이 있기 때문이다.동일한 알고리즘을 보완 그래프의 명시적 표현으로 실행할 경우 훨씬 더 많은 시간이 걸릴 수 있다.따라서, 연구자들은 입력 그래프의 보완에 대해 표준 그래프 계산을 수행하는 알고리즘을 연구했는데, 이는 보완 그래프의 명시적인 구성을 요구하지 않는 암묵적 그래프 표현을 사용한다.특히, 보완 그래프가 훨씬 더 큰 크기를 가질 수 있는 경우에도 주어진 그래프 크기에 선형인 시간 내에 보완 그래프에서 깊이 우선 검색 또는 폭 우선 검색을 시뮬레이션할 수 있다.[8]또한 이러한 시뮬레이션을 사용하여 보완 그래프의 연결에 관한 다른 특성을 계산할 수도 있다.[8][9]
참조
- ^ a b Bondy, John Adrian; Murty, U. S. R. (1976), Graph Theory with Applications, North-Holland, p. 6, ISBN 0-444-19451-7.
- ^ Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, ISBN 3-540-26182-6. 전자판, 4페이지.
- ^ Chudnovsky, Maria; Seymour, Paul (2005), "The structure of claw-free graphs" (PDF), Surveys in combinatorics 2005, London Math. Soc. Lecture Note Ser., vol. 327, Cambridge: Cambridge Univ. Press, pp. 153–171, MR 2187738..
- ^ Lovász, László (1972a), "Normal hypergraphs and the perfect graph conjecture", Discrete Mathematics, 2 (3): 253–267, doi:10.1016/0012-365X(72)90006-4.
- ^ Corneil, D. G.; Lerchs, H.; Stewart Burlingham, L. (1981), "Complement reducible graphs", Discrete Applied Mathematics, 3 (3): 163–174, doi:10.1016/0166-218X(81)90013-5, MR 0619603.
- ^ Golumbic, Martin Charles (1980), Algorithmic Graph Theory and Perfect Graphs, Academic Press, Theorem 6.1, p. 150, ISBN 0-12-289260-7, MR 0562306.
- ^ Golumbic, Martin Charles; Jamison, Robert E. (2006), "Rank-tolerance graph classes", Journal of Graph Theory, 52 (4): 317–340, doi:10.1002/jgt.20163, MR 2242832.
- ^ a b Ito, Hiro; Yokoyama, Mitsuo (1998), "Linear time algorithms for graph search and connectivity determination on complement graphs", Information Processing Letters, 66 (4): 209–213, doi:10.1016/S0020-0190(98)00071-4, MR 1629714.
- ^ Kao, Ming-Yang; Occhiogrosso, Neill; Teng, Shang-Hua (1999), "Simple and efficient graph compression schemes for dense and complement graphs", Journal of Combinatorial Optimization, 2 (4): 351–359, doi:10.1023/A:1009720402326, MR 1669307.