충돌에 의한 절 학습

컴퓨터 과학에서 CDCL(conflict-drived clause learning)은 부울 만족도 문제(SAT)를 해결하기 위한 알고리즘입니다.부울 공식을 지정하면 SAT 문제는 전체 공식이 참으로 평가되도록 변수 할당을 요구합니다.CDCL SAT 솔버의 내부 동작은 DPLL 솔버에서 영감을 받았습니다.CDCL과 DPLL의 가장 큰 차이점은 CDCL의 백 점프가 비연대적이라는 것이다.

분쟁 주도형 조항 학습은 마르케스 실바와 사칼라(1996,^[1]^[2] 1999)와 바야르도 및 슈라그(1997)^[3]에 의해 제안되었다.

배경

부울 만족도 문제

만족도 문제는 연결 정규 형식(CNF)에서 주어진 공식에 대한 만족스러운 할당을 찾는 데 있습니다.

이러한 공식의 예는 다음과 같습니다.

(A가 아님) 또는 (C가 아님) 및 (B 또는 C)

또는 일반적인 ^[4]표기법을 사용하여 다음을 수행합니다.

(\displaystyle (A'\lor C')\land (B\lor C)}

여기서 A, B, C는 부울 변수, $A 、$ $C$ 、 C $、$ $C$ 、 $B 、$ $C$ 、 $A'\lor C'$ $A'\lor C'$ C 、 C 、 C $、$ C 、 C 、 B 、 $B\lor C$ 、 B c C 、 B $B\lor C$ C $A'\lor C'$ 、 C c $A'\lor C'$ C 、 B $B\lor C$ c C c C 、 C $style$ C style C style C $B\lor C$ C style C style C style C style C style C style C $B\lor C$ style C style C style $display$ $style$ \ display stylelor $stylelor b$

이 공식에 대한 만족스러운 과제는 다음과 같다.

A=False, B=False, C=True

두 번째 절(C $\$ $displaystyle$ C $\$ displaystyle C\ $C$ )과 마찬가지로 첫 번째 절(A\displaystyle A $'$ 가 $A'$ 참이므로)도 참이 됩니다.

이 예에서는 3개의 변수(A, B, C)를 사용하고 있으며, 각 변수에는 2개의 할당(True 및 False)이 있습니다.하나는 2 $2^{3}=8$ $2^{3}=8$ $(style$ 2 $^{3$ } $=$ 8)의 $2^{3}=8$ 가능성이 $2^{3}=8$ .이 작은 예에서는 brute-force 검색을 사용하여 가능한 모든 할당을 시도하고 공식을 충족하는지 확인할 수 있습니다.그러나 수백만 개의 변수와 절이 있는 현실적 응용 프로그램에서는 무차별적인 강제 검색이 비현실적입니다.SAT 해결사의 책임은 복잡한 CNF 공식에 다른 휴리스틱을 적용하여 만족스러운 과제를 효율적이고 빠르게 찾는 것입니다.

단위구 규칙(단위 전파)

불만족 절이 False에서 평가된 리터럴 또는 변수를 제외한 모든 것을 포함하는 경우 해당 절이 True가 되려면 자유 리터럴이 True여야 합니다.예를 들어 다음 불만족 절이 A $A=False$ $A=False$ $A=False$ $A=False$ $A=False$ $B=False$ $A=False$ \ $displaystyle$ A $= False$ 및 B $= F$ a $B=False$ $s$ $B=False$ e $\$ $displaystyle$ B = $B=False$ False로 $B=False$ $A=False$ 될 경우 해당 절 $A$ $(A\lor B\lor C)$ $(A\lor B\lor C)$ $(A\lor B\lor C)$ $= True)$ 에 $C=True$ 대해 C $C=True$ $C=True$ $C=True$ 가 $C=True$ 합니다 $.$

unit 구 규칙의 반복 적용은 unit propagation 또는 Boolean Constraint propagation(BCP; 부울 제약 전파)이라고 불립니다.

결의안

2개의 구 $(A\lor B\lor C)$ ' $(A\lor B\lor C)$ ' $(A\lor B\lor C)$ C $displaystyle$ (A $\lor$ B $\lor$ C $)}$ 및 $(A\lor B\lor C)$ $(\neg C\lor D\lor \neg E)$ ( $(\neg C\lor D\lor \neg E)$ ' $(\neg C\lor D\lor \neg E)$ ' $(\neg C\lor D\lor \neg E)$ ' $){$ $displaystyle (\neg$ C $\lor$ D $\lor \neg$ E $(\neg C\lor D\lor \neg E)$ 에 대해 검토합니다.2개의 구를 통합하여 $(\displaystyle\neg$ C $)$ 와 $\neg C$ C $(\displaystyle$ C $C$ 를 모두 삭제한 구 $\lor$ B $\lor$ D $\lor \neg$ E $(A\lor B\lor D\lor \neg E)$ 를 2개의 구의 해결사라고 합니다.

알고리즘.

충돌에 의한 절 학습은 다음과 같이 동작합니다.

변수를 선택하고 True 또는 False를 할당합니다.이를 의사결정 상태라고 합니다.과제를 기억하십시오.
부울 제약 조건 전파(유닛 전파)를 적용합니다.
시사 그래프를 작성합니다.
경합이 있는 경우
1. 충돌의 원인이 된 암시 그래프에서 절단 부분을 찾습니다.
2. 충돌을 초래한 할당을 부정하는 새 절을 도출합니다.
3. 충돌과 관련된 첫 번째 할당된 변수가 할당된 적절한 의사결정 수준으로 비연대적 역추적("백 점프")
그렇지 않으면 모든 변수 값이 할당될 때까지 스텝1부터 계속 진행합니다.

예

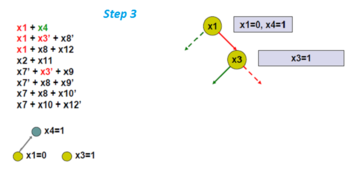
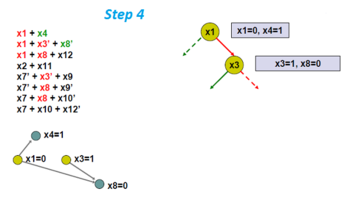
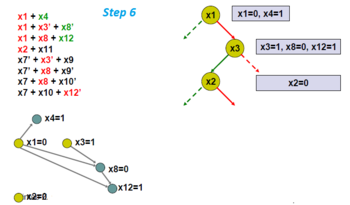
CDCL 알고리즘의 시각적 예:

먼저 분기 변수, 즉 x1을 선택합니다.노란색 원은 임의의 결정을 의미합니다.
이제 단위 전파를 적용합니다. 그러면 x4가 1이어야 합니다(예: True).회색 원은 단위 전파 중 강제 변수 할당을 의미합니다.결과 그래프를 암시 그래프라고 합니다.
다른 분기 변수 x3을 임의로 선택합니다.
단위 전파를 적용하여 새로운 시사 그래프를 찾습니다.
여기서 변수 x8과 x12는 각각 0과 1이 됩니다.
다른 분기 변수 x2를 선택합니다.
시사 그래프를 찾습니다.
다른 분기 변수 x7을 선택합니다.
시사 그래프를 찾습니다.
충돌을 발견했습니다!
이 충돌의 원인이 된 컷을 찾으십시오.절단된 부분으로부터 모순되는 조건을 찾습니다.
이 조건의 부정을 취해서 절로 만들어라.
conflict 절을 문제에 추가합니다.
적절한 의사결정 수준으로의 비연대적 후퇴(이 경우 학습 절에서 리터럴 중 두 번째로 높은 의사결정 수준)
뒤로 점프하고 그에 따라 변수 값을 설정합니다.

완전성

DPLL은 SAT를 위한 건전하고 완전한 알고리즘입니다.CDCL SAT 솔버는 DPLL을 실장하지만 새로운 절을 학습하고 비연대적으로 역추적할 수 있습니다.갈등 분석을 통한 절 학습은 건전성도 완전성도 영향을 미치지 않는다.충돌 분석은 해결 연산을 사용하여 새로운 절을 식별합니다.따라서 학습된 각 절은 해결 단계에 따라 원래의 절 및 기타 학습된 절에서 추론할 수 있다.cN이 새로운 학습절인 경우, is { {cN}도 만족할 수 있는 경우에만 만족합니다.또한 변경된 역추적 스텝은 새로운 ^[5]학습절마다 역추적 정보가 취득되기 때문에 건전성 또는 완전성에 영향을 주지 않는다.

적용들

CDCL 알고리즘의 주요 적용 분야는 다음과 같은 다양한 SAT 솔버입니다.

MiniSAT
Zchaff SAT
Z3
포도당^[6]
ManySAT 등

CDCL 알고리즘은 SAT 솔버를 매우 강력하게 만들어 AI 계획, 생물 정보학, 소프트웨어 테스트 패턴 생성, 소프트웨어 패키지 의존성, 하드웨어 및 소프트웨어 모델 검사, 암호학 등의 실제 응용 분야에서 효과적으로 사용하고 있습니다.

인용된 작품

^ J.P. Marques-Silva; Karem A. Sakallah (November 1996). "GRASP-A New Search Algorithm for Satisfiability". Digest of IEEE International Conference on Computer-Aided Design (ICCAD). pp. 220–227. CiteSeerX 10.1.1.49.2075. doi:10.1109/ICCAD.1996.569607. ISBN 978-0-8186-7597-3.
^ J.P. Marques-Silva; Karem A. Sakallah (May 1999). "GRASP: A Search Algorithm for Propositional Satisfiability" (PDF). IEEE Transactions on Computers. 48 (5): 506–521. doi:10.1109/12.769433.
^ Roberto J. Bayardo Jr.; Robert C. Schrag (1997). "Using CSP look-back techniques to solve real world SAT instances" (PDF). Proc. 14th Nat. Conf. on Artificial Intelligence (AAAI). pp. 203–208.
^ 아래 그림에서 $+(\style$ 는 "or"를 나타내며 곱셈은 "and"를 나타냅니다.
^ Biere, Heule, Van Maaren, Walsh (February 2009). Handbook of Satisfiability (PDF). IOS Press. p. 138. ISBN 978-1-60750-376-7.{{cite book}}: CS1 maint: 여러 이름: 작성자 목록(링크)
^ "Glucose's home page".

레퍼런스

Martin Davis; Hilary Putnam (1960). "A Computing Procedure for Quantification Theory". J. ACM. 7 (3): 201–215. doi:10.1145/321033.321034. S2CID 31888376.
Martin Davis; George Logemann; Donald Loveland (Jul 1962). "A machine program for theorem-proving". Communications of the ACM. 5 (7): 394–397. doi:10.1145/368273.368557. hdl:2027/mdp.39015095248095. S2CID 15866917.
Matthew W. Moskewicz; Conor F. Madigan; Ying Zhao; Lintao Zhang; Sharad Malik (2001). "Chaff: engineering an efficient SAT solver" (PDF). Proc. 38th Ann. Design Automation Conference (DAC). pp. 530–535.
Lintao Zhang; Conor F. Madigan; Matthew H. Moskewicz; Sharad Malik (2001). "Efficient conflict driven learning in a boolean satisfiability solver" (PDF). Proc. IEEE/ACM Int. Conf. on Computer-aided design (ICCAD). pp. 279–285.
프레젠테이션 – "SAT 해결:Lintao Zhang의 "Davis-Putnam에서 Zchaff and Beyond" (프레젠테이션에서 여러 장의 사진을 인용)

[1] J.P. Marques-Silva; Karem A. Sakallah (November 1996). "GRASP-A New Search Algorithm for Satisfiability". Digest of IEEE International Conference on Computer-Aided Design (ICCAD). pp. 220–227. CiteSeerX 10.1.1.49.2075. doi:10.1109/ICCAD.1996.569607. ISBN 978-0-8186-7597-3.

[2] J.P. Marques-Silva; Karem A. Sakallah (May 1999). "GRASP: A Search Algorithm for Propositional Satisfiability" (PDF). IEEE Transactions on Computers. 48 (5): 506–521. doi:10.1109/12.769433.

[3] Roberto J. Bayardo Jr.; Robert C. Schrag (1997). "Using CSP look-back techniques to solve real world SAT instances" (PDF). Proc. 14th Nat. Conf. on Artificial Intelligence (AAAI). pp. 203–208.

[4] 아래 그림에서 $+(\style$ 는 "or"를 나타내며 곱셈은 "and"를 나타냅니다.

[5] Biere, Heule, Van Maaren, Walsh (February 2009). Handbook of Satisfiability (PDF). IOS Press. p. 138. ISBN 978-1-60750-376-7.{{cite book}}: CS1 maint: 여러 이름: 작성자 목록(링크)

[6] "Glucose's home page".

[1]

[2]

[3]

[4]

[5]

[6]

Search