코슈 함수

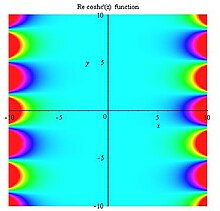
수학에서 코슈 함수는 ^[1]광학 산란, 하이젠베르크 스파크타임^[2], 쌍곡 기하학에 관한 논문에서 자주 나타난다.^[3]로^[4]^[5] 정의된다.

\operatorname {Coshc}(z)={\frac {\cosh(z)}{z}}

다음과 같은 미분방정식의 해법이다.

w(z)z-2{\frac {d}{dz}w(z)-z{d^{d^{2}}:{dz^{2}}(z)=0

코쉬 2D 플롯

코슈(z) 2D 플롯

복잡한 평면의 가상 부품: ${\displaystyle \operatorname {Im} \left({\frac {\cosh(x+iy)}{x+iy}\오른쪽)$
복잡한 평면의 실제 부분: ${\displaystyle \operatorname {Re} \left({\frac {\cosh(x+iy)}{x+iy}\오른쪽)$
절대 규모: $왼쪽 {\displaystyle \frac {\cosh(x+iy)}{x+iy}\오른쪽 }$
1차 파생상품: ${\displaystyle {\frac {\sinh(z)}{z}-{\frac {\cosh(z)}{z^{2}}:$
파생상품의 실제 부분: $-\operatorname {Re} \좌측(-{\frac {1-(\cosh(x+iy)))^{2}}:{x+iy}+{\frac {\cosh(x+iy)}{(x+iy)^{2}}:}\오른쪽)$
파생상품의 가상부분: $-\operatorname {Im} \left(-{\frac {1-(\cosh(x+iy)))^{2}}:{x+iy}+{\frac {\cosh(x+iy)}{(x+iy)^{2}}:}\오른쪽)$
파생상품의 절대가치: $\좌측 -{\frac {1-(\cosh(x+iy)))^{2}}:{x+iy}+{\frac {\cosh(x+iy)}{(x+iy)^{2}}}\오른쪽$

기타 특수 기능 측면에서

$\operatorname {Coshc}(z)={\frac {(iz+1/2\,\pi ){\rm {M}(1,2,i\pi -2z)}}{e^{(i/2)\pi -z}z}}}$
$\operatorname {1/2}={\frac {1}{1}2}}:\,{\frac {(2\,iz+\pi )\운영자 이름 {HeunB} \좌측(2,0,0,0,{\sqrt {1}{\sqrt{1/2\i\pi-z}\오른쪽)}}{e^{1/2\,i\pi -z}}}$
$\operatorname {Coshc}(z)={\frac {-i(2\,iz+\pi ){{\rm {\mathbf {W}hitakerM}(0,\,\,1/2,\,i\pi -2z)}}}{(4iz+2\}}}}}}}})$

\operatorname {Coshc} z\approx \left(z^{-1}+{\frac {1}{2}}z+{\frac {1}{24}}z^{3}+{\frac {1}{720}}z^{5}+{\frac {1}{40320}}z^{7}+{\frac {1}{3628800}}z^{9}+{\frac {1}{479001600}}z^{11}+{\frac {1}{87178291200}}z^{13}+O(z^{15})\right)

\operatorname {Coshc} \left(z\right)={\frac {23594700729600+11275015752000\,{z}^{2}+727718024880\,{z}^{4}+13853547000\,{z}^{6}+80737373\,{z}^{8}}{147173\,{z}^{9}-39328920\,{z}^{7}+5772800880\,{z}^{5}-522334612800\,{z}^{3}+23594700729600\,z}}

코슈 복근 콤플렉스 3D

코슈 임 콤플렉스 3D 플롯

Coshc Re 복합 3D 플롯

코슈'(z) Im complex 3D 플롯

Coshc'(z) Re complex 3D 플롯

코슈(z) 복근 복합 3D 플롯

코쉬'(x) 복근 밀도 그림

코슈'(x) 임 밀도 그림

Coshc'(x) Re 밀도 그림

^ PN Den Outer, TM Nieuwenhuizen, A Lagendijk, 다중 스캐터 매체 내 물체의 위치, JOSA A, 10, 문제 6, 페이지 1209–1218(1993)
^ T Körpinar, Heisenberg spacetime, International Journal of theory Physics, 2014 Springer에서 생체 입자의 에너지를 최소화하기 위한 새로운 특성화
^ Nilgün Sönmez, 국제 수학 포럼, 4, 2009, No. 38, 1877 1881 쌍곡 기하학에서 오일러 정리의 삼각법 증명
^ JHM 10 티제 분캄프, J van Dijk, L 류, 보존법 제도에 대한 완전한 플럭스 제도의 확장, J Sci Comput (2012) 53:552–568, DOI 10.1007/s10915-012-9588-5
^ 와이스슈타인, 에릭 W. "코쉬 함수"MathWorld—Wolfram 웹 리소스.http://mathworld.wolfram.com/CoshcFunction.html^{[permanent dead link]}