평형 상수 결정

평형 상수는 화학 평형을 정량화하기 위해 결정된다. 평형 상수 K가 농도 지수로 표현될 때,

${\displaystyle K={\frac {\mathrm {[S]} ^{\sigma }\mathrm {}\t] ^{\tau }\cdots }{\mathrm {[A]} ^{\alpha }\beta }}}}}cdots}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

활동 지수가 일정하다는 것을 암시한다. 이 가정이 유효하려면 평형 상수는 이온 강도가 상대적으로 높은 매체에서 결정되어야 한다. 이것이 불가능할 경우 가능한 활동 변동을 고려해야 한다.

위의 평형식은 평형상태의 화학종 농도[A], [B] 등의 함수다. 평형 상수 값은 이러한 농도 중 하나를 측정할 수 있는 경우 결정할 수 있다. 일반적인 절차는 반응제 분석 농도를 알고 있는 일련의 용액에 대해 해당 농도를 측정하는 것이다. 일반적으로 적정 용기는 적정 용기에 있는 하나 이상의 반응제 및 뷰렛에 있는 하나 이상의 반응제로 적정화를 수행한다. 초기 반응 용기와 뷰렛에 있는 반응물질의 분석 농도를 알면, 모든 분석 농도는 첨가된 적정량의 부피(또는 질량)의 함수로 도출될 수 있다.

평형 상수는 실험 데이터를 평형계의 화학적 모델로 가장 잘 적합시켜 도출할 수 있다.

실험 방법

크게 네 가지 실험 방법이 있다. 덜 일반적으로 사용되는 방법은 Rossotti와 Rossotti를 참조하십시오.^[1] 모든 경우에 경쟁 방식을 사용하여 범위를 확장할 수 있다. 이 방법의 적용 예는 팔라듐()에서 찾을 수 있다.II) 청산가리.

전위차계 측정

A종의 자유농도[A] 또는 활동성 {A}은 유리 전극과 같은 이온 선택 전극을 사용하여 측정한다. 활동 표준을 사용하여 전극을 교정할 경우 네른스트 방정식이 형태에 적용되는 것으로 가정한다.

${\displaystyle E=E^{0}+{\frac {RT}{nF}\ln \mathrm{\{A\}}}}}$

여기서 E는⁰ 표준 전극 전위다. 알려진 pH의 버퍼 용액을 교정에 사용할 경우 미터기 판독값은 pH가 된다.

${\displaystyle \mathrm {pH} ={\frac {nF}{RT}}\왼쪽(E^{0}-E\오른쪽)}$

298 K에서 1 pH 단위는 대략 59 mV와 같다.^[2]

예를 들어 강한 산-강 염기 적정을 통해 알려진 농도의 용액으로 전극을 교정할 때 수정된 네른스트 방정식이 가정된다.

${\displaystyle E=E^{0}+s\log _{10}\mathrm {[A]} }$

여기서 s는 경험적 경사 계수다. 알려진 수소 이온 농도의 용액은 붕소에 대한 강한 산의 표준화에 의해 준비될 수 있다. 수소 이온 농도의 일차 표준으로 일정하게 끓는 염산을 사용할 수도 있다.

범위 및 제한

가장 널리 사용되는 전극은 유리 전극으로 수소 이온에 선택적이다. 이것은 모든 염기성 평형증에 적합하다. 약 2와 11 사이의 로그₁₀ β 값은 유리 전극을 사용한 전위차계 적정에 의해 직접 측정할 수 있다. 이 엄청난 범위의 안정성 상수 값(ca. 100 ~ 10¹¹)은 전극의 로그 응답 때문에 가능하다. 제한은 네른스트 방정식이 매우 낮거나 매우 높은 pH에서 분해되기 때문에 발생한다.

계산된 평형 상수가 의존하는 측정을 얻기 위해 유리 전극을 사용할 경우 계산된 파라미터의 정밀도는 전극 내 액체 접합 전위의 변동과 같은 이차 효과에 의해 제한된다. 실제로 ±0.001보다 높은 로그 β에 대한 정밀도를 얻는 것은 사실상 불가능하다.

분광도 측정

흡광도

Beer-Lambert 법이 적용되는 것으로 가정한다.

${\displaystyle A=l=sum {\barepsilon c}}$

여기서 l는 광학 경로 길이, ε은 단위 경로 길이에서 어금니 흡광도, c는 농도다. 그 종들 중 하나 이상이 흡수에 기여할 수 있다. 원칙적으로 흡광도는 하나의 파장에서만 측정할 수 있지만, 현재의 연습에서는 완전한 스펙트럼을 기록하는 것이 일반적이다.

형광(발광) 강도

산란 광도는 종 농도의 선형 함수라고 가정한다.

$\displaystyle I=\sum \varphi c}$

여기서 φ은 비례 상수다.

범위 및 제한

흡광도와 발광 : 통상적으로 4의 로그₁₀ β에 대한 상한을 인용하여 측정의 정밀도에 해당하지만, 효과가 얼마나 강한가에 따라 달라지기도 한다. 기여 종의 스펙트럼은 서로 명확하게 구별되어야 한다.

NMR 화학 시프트 측정

화학적 교환은 NMR 시간 척도에서 빠른 것으로 가정한다. 개별 화학적 변화 Δ는 기여 종에서 핵의 변화 Δ의 몰-굴절 가중 평균이다.

${\displaystyle {\bar{\i}}={\frac {\sum x_{i}\properties _{i}}}{{i}}}}}}}}}$

예: 구연산 내 히드록실 그룹의_a pK는 C 화학적 시프트 데이터에서 14.4로 결정되었다. 이 결정에 전위차 측정법이나 자외선 분광법을 사용할 수 없다.^[3]

범위 및 제한

화학적 이동 측정의 제한된 정밀도 또한 로그₁₀ β에 약 4의 상한을 둔다. 직경 시스템으로 제한된다. ¹HNMR은 HO의₂ 화합물 용액과 함께 사용할 수 없다.

칼로리 측정

1:1 인덕트에 대한 K와 ΔH의 동시 측정은 등온 적정 열량측정을 사용하여 일상적으로 수행된다. 보다 복잡한 시스템에 대한 확장은 적절한 소프트웨어의 가용성에 의해 제한된다.

범위 및 제한

현재 이용 가능한 증거가 불충분하다.

경쟁 방식

경기 방법은 안정성 상수 값이 너무 커서 직접 방법으로 결정할 수 없을 때 사용할 수 있다. 슈바르첸바흐가 금속 이온으로 EDTA 복합체의 안정성 상수를 결정하는 데 처음 사용하였다.

단순성을 위해 안정성 상수 K ${\displaystyle A_{}}$ B ${\$다른 시약 B와 함께 시약 A의 바이너리 콤플렉스 AB$}$

${\displaystyle K_{AB}={\frac {[AB]}{[A][B]}}}}}$

여기서 [X]는 주어진 구성의 용액에서 종 X의 평형 농도를 나타낸다.

A로 약한 콤플렉스를 형성하는 리간드 C를 선택한다 안정성 상수 K는_AC 직접적 방법에 의해 결정될 만큼 작다. 예를 들어 EDTA 복합체의 경우 A는 금속 이온이고 C는 디에틸렌트리아민과 같은 폴리아민일 수 있다.

${\displaystyle K_{AC}={\frac {[]AC]}{[A][C]}}}}$

안정성 상수, 경기 반응에 대한 K

$AB+C}$

라고 표현할 수 있다.

${\displaystyle K={\frac {[AB][C]}{[]AC][B]}}}$

그 뒤를 잇는다.

${\displaystyle K_{AB}=K\time K_{AC}$

여기서 K는 경기 반응에 대한 안정성 상수다. 따라서 안정성 상수 $K{\displaystyle {}_{}}$ ${\displaystyle A_{}}$ ${\displaystyle B_{}}$ ${\$$AB}}$은(는) ${\displaystyle K_{}}$와 $K{\displaystyle {}_{}}$ A ${\displaystyle C_{}}$의 실험적으로 결정된 값 ${\$ 스타일 $K_{$에서 도출할$$ 수 있다.$AC}$ .$$

계산 방법

수집된 실험 데이터는 일련의 데이터 점을 구성하는 것으로 가정한다. 각 ith 데이터 지점에서, 반응제, T(i_A), T_B(i) 등의 분석농도는 이러한 분석농도 중 하나 이상에 따라 달라지는 측정량 y와_i 함께 알려져 있다. 일반적인 계산 절차에는 네 가지 주요 구성 요소가 있다.

1. 평형주의 화학적 모델 정의
2. 각 용액 내 모든 화학종 농도의 계산
3. 평형 상수의 미세화
4. 모델 선택

호스트-게스트 종과 같은 1:1 복합체 형성을 위한 평형 상수의 값은 전용 스프레드시트 애플리케이션인 Bindfit를 사용하여 계산할 수 있다.^[4] 이 경우 2단계는 비 반복적 절차로 수행할 수 있으며 3단계에 대해 사전 프로그래밍된 절차인 Solver를 사용할 수 있다.

화학 모델

화학적 모델은 반응 혼합물에 첨가된 반응 물질과 그것들로부터 형성되는 복잡한 종들 둘 다 용액에 존재하는 화학 종들의 집합으로 구성된다. A, B...에 의해 반응제를 나타내는 각각의 복잡한 종은 반응체를 형성하는 반응물질의 특정한 조합과 관련된 확률계수 계수로 지정된다.

${\$$A}+{\mathit{q}B\cdots <=>$$A_{\mathit {p}}B_{\mathit {q}}\cdots }}}$: ${\displaystyle \beta _{pq\cdots }={\frac {[{\ce {A}}_{p}{\ce {B}}_{q}\cdots ]}{[{\ce {A}}]^{p}[{\ce {B}}]^{q}\cdots }}}$

범용 컴퓨터 프로그램을 사용할 때는 위와 같이 누적 연결 상수를 사용하는 것이 보통이다. 전기요금은 이와 같은 일반적인 표현에는 나타나 있지 않으며 표기법의 단순성을 위해 특정 표현에서 생략하는 경우가 많다. 사실, 전하가 평형 과정과 관련이 없다는 것은 모든 시스템에서 전체적인 전기 중립성에 대한 요건이 있다는 것을 의미한다.

수용액과 함께 양성자(수소이온)와 수산화이온의 농도는 물의 자가 분해에 의해 제한된다.

- +- ${\$ce {${\displaystyle \frac{{}^{}}{}}$ $<=> H+$+ $OH-}}$: $K{\displaystyle {}_{}^{}}$ ${\displaystyle {W\mathrm{}}_{}^{}}$ ${\displaystyle {{}^{}}_{}^{{}^{}}}$=${\displaystyle \frac{}{}}$[ H${\displaystyle \frac{{}^{}}{}}$+ ${\displaystyle \frac{{}^{}}{}}$[ ${\displaystyle \frac{{O\mathrm{}}_{}}{}}$ -${\displaystyle \frac{{}^{}}{}}$ [${\displaystyle \frac{}{}}$O ${\displaystyle \frac{{}_{}}{}}$ - ${\displaystyle \frac{]}{}}$ ${\$ {frac$}$$H^{+}][OH^{-}]}{{[$$H_{2}O]}}}$

묽은 용액으로 물의 농도를 일정하게 가정하므로 평형 표현은 물의 이온성 생산물의 형태로 쓰여진다.

${\displaystyle K_{\mathrm {W}={\ce {[H+]}}}}][{\ce {OH-}}\,}$

H와⁺ OH를⁻ 모두 반응제로 간주해야 하는 경우, 그 중 하나는 반응물질의 농도가 다른 반응물질의 농도로부터 유도된다는 것을 명시함으로써 모델에서 제거된다. 보통 수산화 이온의 농도는 다음과 같다.

${\displaystyle [{\ce {OH-}}={\frac {K_{\ce{W}}{{W}}{{\ce {H+}}}}}}},}$

이 경우 수산화물 형성을 위한 평형 상수는 양성자에 대한 스토이치계수 -1, 다른 반응체에 대한 0을 갖는다. 이것은 수용액의 모든 양성자와 특히 가수분해 상수에 중요한 의미를 가진다.

농도를 무시할 수 있는 것으로 간주되는 종을 모형에서 생략하는 것은 꽤 흔한 일이다. 예를 들어, 일반적으로 반응제 및/또는 복합체와 일정한 이온 강도를 유지하는 데 사용되는 전해질 또는 일정한 pH를 유지하는 데 사용되는 완충제 사이에 교호작용이 없다고 가정한다. 이러한 가정은 정당화될 수도 있고 정당화될 수 없을 수도 있다. 또한, 다른 복잡한 종은 존재하지 않는다고 암묵적으로 가정한다. 콤플렉스가 잘못 무시될 경우 체계적인 오류가 계산에 도입된다.

평형 상수 값은 대개 데이터 출처를 참조하여 초기에 추정한다.

지정 계산

분화 계산은 반응제 A, B 등의 분석농도, T_A, T 등을_B 알고 평형계통에 있는 모든 종의 농도를 계산하는 계산이다. 이는 질량 균형에 대한 비선형 방정식 집합을 해결하는 것을 의미한다.

${\displaystyle {\begin{aigned}{\ce {T_{A}}}&=[{\ce {A}}]+\sum _{1,nk}p\beta _{pq\cdots }[{\ce {A}}]^{p}[{\ce {B}}]^{q}\cdots \\{\ce {T_{B}}}&=[{\ce {B}}]+\sum _{1,nk}q\beta _{pq\cdots }[{\ce {A}}]^{p}[{\ce {B}}]^{q}\cdots \\etc.\end{정렬}}}$

자유농도 [A], [B] 등의 경우 pH(또는 등가 e.m.f, E.)를 측정할 때 수소 이온의 자유농도 [H]를 측정값에서 다음과 같이 구한다.

${\displaystyle [\mathrm {H} ]=10^{-\mathrm {pH} }}$ or ${\displaystyle [\mathrm {H} ]=10^{\mathrm {\frac {E-E^{0}}{2.303$$RT/nF}}}}$

다른 반응물질의 자유농도만 계산된다. 복합체의 농도는 화학적 모델을 통한 자유농도에서 도출된다.

일부 저자는^[5][6] 계량계수가 관련 반응물질의 경우 1이고 다른 모든 반응물질의 경우 0인 식별(단위) β 상수를 선언하여 총합에 자유반응제 용어를 포함한다. 예를 들어, 2개의 시약을 사용하면 질량 균형 방정식이 더 간단한 형태를 가정한다.

${\displaystyle {\reasoned}T_{\ce {A}&=\sum _{0,nk}p\beta_{pq}[{\ce {A}]^{p}[{\ce {B}]^{q}\[4pt]T_{\ce{B}&=\sum _{0,nk}q\beta_{pq}[{\ce {A}}}^{p}[{\ce {B}}]^{q}\\ended}}}}}}}}$

${\displaystyle \properties _{10}=\properties _{01}=1}$

이러한 방식으로 자유반응제를 포함한 모든 화학종들은 스토이치계수에 의해 지정된 반응물질의 조합으로부터 형성되어 동일한 방식으로 처리된다.

적정 시스템에서 각 적정 지점의 반응제 분석 농도는 초기 조건, 부레트 농도 및 부피로부터 얻는다. ith 적정 지점에서 반응제 R의 분석(총) 농도는 다음과 같다.

${\displaystyle T_{{\ce{R}}={\frac {{\ce{R}_{0}+v_{0}{\ce {[R]}{v_{0}+v_{i}}}}}}}{v_{0}}}}}}}}}}}}}}}}{{i}}}}}}}}}}}}}}}}}}}}}$

여기서 R은₀ 적정 용기의 R의 초기 양이고, v는₀ 초기 볼륨이고, [R]는 뷰렛의 R 농도, v는_i 추가된 볼륨이다. 뷰렛에 존재하지 않는 반응물질의 뷰렛 농도는 0으로 간주된다.

일반적으로, 이러한 비선형 방정식을 푸는 것은 자유 농도의 범위가 다양하기 때문에 만만치 않은 난제를 제시한다. 초기에는 자유 농도의 값을 추정해야 한다. 그런 다음, 이러한 값들은 대개 뉴턴-래프슨 반복을 통해 정제된다. 자유농도의 로그는 자유농도 자체보다는 정제될 수 있다. 자유농도의 로그의 정교화는 자유농도에 비부정성 제약조건을 자동으로 부과할 수 있는 추가적인 장점이 있다. 일단 자유 반응제 농도를 계산하면, 복합체의 농도는 그것들과 평형 상수로부터 도출된다.

자유반응제 농도는 평형 상수 미세화 과정에서 암묵적 매개변수로 간주될 수 있다는 점에 유의한다. 그러한 맥락에서 자유 농도의 값은 공정의 모든 단계에서 질량 균형 조건을 적용하도록 강제함으로써 제약을 받는다.

평형 상수 미세화

정제 공정의 목적은 실험 데이터에 가장 적합한 평형 상수 값을 찾는 것이다. 이는 일반적으로 비선형 최소 제곱법을 통해 객관적 함수 U를 최소화함으로써 달성된다. 먼저 잔차를 다음과 같이 정의한다.

${\displaystyle r_{i}=y_{i}^{\text}{{i}}^{\text}}}}$

그런 다음 가장 일반적인 목표 함수는 다음과 같다.

${\displaystyle U=\sum _{i}\sum _{j}r_{i}W_{ij}r_{j}\,}$

가중치 행렬 W는 이상적으로는 관측치의 분산-공분산 행렬의 역행이어야 한다. 이런 사실이 알려진 것은 드물다. 단, U의 기대값은 1이며, 이는 실험 오차 내에 데이터가 적합됨을 의미한다. 대부분의 경우 대각선 요소만 알려져 있으며, 이 경우 목표 기능은 다음과 같이 단순화된다.

$U=\sum _{i}W_{i}r_{i}^{2}}$

w_ij = 0인 경우 j ≠ i. 단위 가중치 W_ii = 1을 사용하는 경우가 많지만, 이 경우 U의 기대값은 실험 오차의 평균 제곱이다.

최소화는 가우스-뉴턴 방법을 사용하여 수행할 수 있다. 첫째, 목표 함수는 초기 매개변수 집합 p에 대한 1차 Taylor 시리즈 확장으로 대략 계산하여 선형화한다.

${\displaystyle U=U^{0}+\sum _{i}{\frac {\partial U}{\partial p_{i}}\delta p_{i}}}}{i}}}}}}$

그 증식 δpi 해당 초기 매개 변수에 더하UU0보다 적다.그 최소한이 파생{.sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den .mw-parser-output.Border-top:단순히 야코비안 매트릭스의 요소에 관련된 1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}∂U/∂pi, J.

${\displaystyle J_{jk}={\frac {\partial y_{j}^{\mathrm {calc}}}}{{\partial p_{k}}}}}}}}}}}$

여기서 p는_k 정교함의 k번째 매개변수로서 0과 같다. 하나 이상의 평형 상수가 정교함의 매개변수가 될 수 있다. 그러나 y로 대표되는 측정된 수량(위 참조)은 평형 상수의 관점에서가 아니라, 이 매개변수의 암묵적 함수인 종 농도의 측면에서 표현된다. 그러므로 야코비안 원소는 암묵적인 분화를 이용하여 얻어야 한다.

매개변수 증가 Δp는 최소 ∂U/∂p = 0인 조건으로부터 도출된 정상 방정식을 풀어서 계산한다.

${\displaystyle {\reft(J^{\mathrm {T} }WJ\right)\delta p=J^{\mathrm {T}Wr}}}}}$

증분 Δp는 파라미터에 반복적으로 추가된다.

${\displaystyle \mathbf {p} ^{n+1}=\mathbf {p} ^{n}+\mathbf {p}}$

여기서 n은 반복 번호다. 종 농도와 y^calc 값은 모든 데이터 지점에서 다시 계산된다. U의 유의미한 감소가 이루어지지 않을 때까지, 즉 수렴 기준이 충족될 때까지 반복한다. 그러나 업데이트된 매개변수가 목표 함수의 감소를 초래하지 않는 경우, 즉, 차이가 발생하면 증분 계산을 수정해야 한다. 가장 간단한 수정은 계산된 증가분의 일부, f, 이른바 시프트 커팅(shift cuting)을 사용하는 것이다.

${\displaystyle \mathbf {p} ^{n+1}=\mathbf {p} ^{n}+f\mathbf {\mathbf} }}$

이 경우 시프트 벡터 Δp의 방향은 변하지 않는다. 반면에 보다 강력한 레벤베르크-마르콰르트 알고리즘으로, 시프트 벡터는 정상 방정식을 수정하여 가장 가파른 하강 방향으로 회전한다.

${\displaystyle \mathbf {\left(J^{\mathrm {T} }WJ+\lambda I\right)\delta p=J^{\mathrmatrm {T}Wr}}}$

여기서 λ은 마르콰르트 매개변수이고 나는 정체성 행렬이다. 다른 차이점 처리 방법이 제안되었다.^[6]

NMR 및 분광학 데이터와 관련하여 특별한 문제가 발생한다. 후자의 경우 관측량은 흡광도 A이며, Beer-Lambert 법칙은 다음과 같이 표기할 수 있다.

${\displaystyle A_{\lambda }=l\sum(\varepsilon _{pq.}}}_{\boda }c_{pq..}}$

농도 c가 알려져 있다고 가정할 때 주어진 파장에서 흡광도 A, $\lambda {\displaystyle }$ ${\displaystyle \lambda$ $\},$ 경로 $l{\displaystyle }$ ${\displaystyle l}$이$$어금니 흡광도의 선형 함수인 것을 알 수 있다. 1cm 경로 길이 포함, 행렬 표기법

${\displaystyle \mathbf{A} ={\boldsymbol {\barepsilon }}\mathbf {C} \,}$

알 수 없는 어금니 흡수성의 계산에는 두 가지 접근법이 있다.

(1) ε 값은 최소화의 매개변수로 간주되며, 그 기초로 Jacobian을 구성한다. 단, ε 값 자체는 선형 최소 제곱에 의해 각 미세화 단계에서 계산된다.

${\displaystyle {\boldsymbol}}}}=\mathbf {\좌(C^{\mathrm {T} }C\우)^{-1}C^{\mathrm {T}}A}}}$

규격 획득을 위해 평형 상수의 정제된 값을 사용한다. 행렬

${\displaystyle \mathbf {\왼쪽(C^{T}C\오른쪽)^{-1}C^{T}} }$

사이비 종교의 예야

골럽과 페레이라는^[7] 정상적인 방정식을 풀어서 어금니 흡수성과 평형 상수 모두에 대한 매개변수 증가를 계산할 수 있도록 의사상환이 어떻게 분화될 수 있는지를 보여 주었다.

(2) Beer-Lambert 법은 다음과 같이 쓰여 있다.

${\displaystyle \mathbf {\boldsymbol {\varepsilon }} _{\lambda }=\mathbf {A} _{\lambda ^{-1}\mathbf {C} \,},}$

모든 "색깔" 종의 알려지지 않은 어금니 흡착은 한 번에 한 파장씩 선형 최소 제곱의 비반복적 방법을 사용하여 발견된다. 계산은 $매트릭스{\displaystyle \mathbf{}}$ C ${\$ {$C}$에서 종의 농도 값을 계산하기 위해 정제 주기마다 한 번씩 수행된다$.$

파라미터 오류 및 상관 관계

목표 함수의 최소값인 U에 가까운 영역에서 시스템은 선형 최소 제곱 시스템에 근사치한다.

${\displaystyle \mathbf {p=\left(J^{\mathrm {T}{{WJ\right)^{-1J^{\mathrm {T}{Wy^{\mathrm {obs}}}}}}}}}}}}}}}}}}}}}}}}$

따라서 매개변수 값은 관측된 데이터 값의 (대략) 선형 결합이며 매개변수 p의 오류는 선형 공식을 사용하여 관측치^obs y로부터 오차 전파를 통해 얻을 수 있다. 관측치에 대한 분산-공분산 행렬을 σ으로^y 표시하고 σ로^p 모수의 행렬을 표시하도록 한다. 그러면.

${\displaystyle \mathbf {\Sigma ^{p}=\왼쪽(J^{\mathrm {T}{{WJ\right)^{-1}J^{\mathrm {T}{}W\Sigma ^{y}W^{\mathrm {T} }J(J^{\mathrm {T} }WJ)^{-1}}}$

W = (RW^y)⁻¹이면 다음과 같이 단순화된다.

${\displaystyle \mathbf {\Sigma ^{p}=\왼쪽(J^{\mathrm {T}}{WJ\right)^{-1}}}$

대부분의 경우 관측치의 오류는 상관 관계가 없으므로 σ은^y 대각선이다. 만일 그렇다면 각 가중치는 해당 관측치의 분산에 대한 역수여야 한다. 예를 들어, 전위차적 적정화에서 적정 지점의 중량 k는 다음과 같이 주어질 수 있다.

${\displaystyle W_{k}={\frac {1}{\sigma _{E}^{2}+\왼쪽({\frac {\partial e}{\partial v}\오른쪽)_{k}^{2}\bma _{v}^{2}}:$

여기서 σ은_E 전극 전위 또는 pH의 오차, (∂E/∂v)
_k는 적정곡선의 기울기, σ은_v 부피의 오차다.

단위 중량을 사용할 때(W = I, p = (JJ)^T−1Jy^T) 실험 오차가 상관관계가 없고 모두 같다는 것을 암시한다: σ^y = σI², 여기서 σ은² 단위 중량의 관측치 분산으로 알려져 있으며, 나는 식별 행렬이다. 이 경우 σ은² 다음과 같이 근사치한다.

${\displaystyle \sigma ^{2}={\frac {U}{n_{\mathrm {d}{}-n_{\mathrm {p}}}}}}}}}}}}}$

여기서 U는 목표함수의 최소값이고 n과_d n은_p 각각 데이터와 파라미터의 수입니다.

${\displaystyle \mathbf{\Sigma ^{p}} ={\frac {U}{n_{d}}}-n_{\mathrm {p}}}}}\좌측(\mathbf {J}^{\mathb}{}}{J} \mathbf {J}오른쪽)^{-1}^{-1}:{-1}:{-1}:{-1}$

모든 경우에, 모수_i p의 분산은^p
_ii by에 의해 주어지고, 모수_i p와 p_j 사이의 공분산은 σ에^p
_ij 의해 주어진다. 표준 편차는 분산의 제곱근이다. 이러한 오차 추정치는 측정에서 랜덤 오차만 반영한다. 매개변수의 진정한 불확실성은 체계적 오류(정의상으로는 계량화할 수 없음)가 존재하기 때문에 더 크다.

관측치가 상관 관계가 없을 수 있지만 모수는 항상 상관 관계가 있다는 점에 유의하십시오.

파생 상수

누적 상수가 정제된 경우, 종종 그것들로부터 단계적 상수를 도출하는 것이 유용하다. 일반적인 절차는 관련된 모든 상수에 대한 정의 식을 기록한 다음 농도를 동일시하는 것이다. 예를 들어, 구연산과 같은 트리파스산 LH에서₃ 양성자 하나를 제거하기 위해 pKa를 추출하려고 한다고 가정합시다.

${\displaystyle{\begin{정렬}{\ce{L^3-}}+{\ce{여기서<>=>.}}){\ce{LH^2-}}&:)[{\ce{LH^2-}}]=\beta _ᆳ[{\ce{L^3-}}][{\ce{여기서}}]\\{\ce{L^3-}}+{\ce{2H+<>=>.}}){\ce{LH2^-}}&:)[{\ce{LH2^-}}]=\beta _ᆷ[{\ce{L^3-}}][{\ce{여기서}}]^{2}\\{\ce{L^3-}}+{\ce{3H+<>=>.}}){\ce{LH3}}&:)[{\ce{LH3}}]=\beta _{13}는 경우에는{\ce{L^3-}.}][{\ce{여기서}}]^{3}\end{정렬}}}$

LH₃ 형성을 위한 단계적 연결 상수는 다음과 같다.

${\displaystyle}\ce {{}LH2^{-}+H+<=>LH3\ ;\quad \[LH3]}}}}=K[{\ce {LH2^{-}}][{\ce {H+}}}}}}$

이₃ 식에 LH와⁻
₂ LH의 농도에 대한 식을 대입한다.

${\displaystyle \beta_{13}[{\ce {L^3-}}][{\ce {H+}}}^{3}=K\beta _{12}[{\ce {L^3-}}][{\ce {H+}}}}^{\ce {H+}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}"$

언제

${\displaystyle \beta _{13}=K\beta _{12};K={\frac {\beta _{13}{\beta _{12}},}$

그리고_a pK = -log₁₀ 1/K이기 때문에 그 값은

${\displaystyle {\p}K_{{\ce {a1}}=\log _{10}\beta_{13}\log _{10}\beta _{12}\,}$

${\displaystyle {\p}K_{\ce {a2}}=\log _{10}\beta_{12}\log _{10}\beta _{11}\,}$

${\displaystyle {\p}K_{\ce {a3}=\log _{10}\beta _{11}\,}$

pK 및 로그 β에 대한 역방향 번호를 기록해 두십시오. 단계적 상수에 대한 오차를 계산할 때 누적 상수가 상관관계가 있다는 사실을 설명해야 한다. 오류 전파별

${\displaystyle \sigma_{K}^{2}=\sigma _{\beta_{12}}+\sigma _{\beta_{13}}^{\beta-2}\sigma _{\13}}}}}$

그리고

${\displaystyle \sigma _{\log _{10}K}={\frac {\sigma _{K}}}}$

모델 선택

정교화가 완료되면 결과를 점검하여 선택한 모델이 허용 가능한지 확인해야 한다. 일반적으로 모형은 실험 오차 내에서 데이터가 적합될 때 허용되지만, 판단을 내리기 위해 사용할 단일 기준이 없다. 다음 사항을 고려해야 한다.

목적함수

실험 오차 추정치에서 가중치가 정확하게 도출된 경우 U/n_d - n의_p 기대값은 1이다.^[8] 따라서 이것은 적합도를 절대적으로 나타내는 지표이기 때문에 실험 오차를 추정하고 그것으로부터 합리적인 가중치를 도출하는 것은 매우 유용하다.

단위 가중치를 사용할 경우 모든 관측치의 분산이 동일하다는 것을 암시한다. U/n_d - n은_p 그 분산과 같을 것으로 예상된다.

매개 변수 오류

스태빌리티 상수의 오차가 실험 오차에 대략 맞도록 해야 한다. 예를 들어, pH 적정 데이터를 사용하여 pH를 소수점 2자리까지 측정할 경우 로그₁₀ β의 오차는 0.01보다 크지 않아야 한다. 존재하는 종의 성질을 미리 알 수 없는 탐색적 작업에서는 여러 가지 다른 화학적 모델을 시험하고 비교할 수 있다. 평형 상수의 최적 추정치의 불확실성이 σ보다_pH 다소 또는 심지어 상당히 클 수 있는 모델이 있을 것이며, 특히 그러한 상수들이 비교적 작은 종의 형성을 지배하고 있지만, 얼마나 큰 크기가 허용될 수 있는지에 대한 결정은 주관적이다. 비교적 불확실한 평형도를 모형에 포함시킬지 여부와 일반적으로 경쟁 모델들의 비교에 관한 결정 과정은 객관적일 수 있으며 해밀턴에 의해 윤곽이 잡혔다.^[8]

잔차 분포

최소 U에서는 시스템을 선형 시스템과 근사하게 비교할 수 있으며, 단위 중량의 경우 잔차는 다음과 같은 방법으로 관측치와 관련이 있다.

${\displaystyle \mathbf {r=y^{\mathrm {obs}}-J\왼쪽(J^{\mathrm {T}}오른쪽)^{-1}J^{\mathrm {T}{}y^{}}}{}mathrmatrm {obs}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

대칭, 공차 행렬 J(JT)^T−1J는 통계 문헌에서 모자 행렬 H로 알려져 있다. 그러므로,

${\displaystyle \mathbf {r=\left(I-H\right)y^{\mathrm {obs}}}}}$

그리고

${\displaystyle \mathbf {M^{r}=\왼쪽(I-H\오른쪽)M^{y}\왼쪽(I-H\오른쪽) }$

여기서 I는 ID 행렬이고 M과^r M은^y 각각 잔차 및 관측치의 분산-공분산 행렬이다. 이는 관측치가 상관 관계가 없을 수 있더라도 잔차는 항상 상관 관계가 있음을 보여준다.

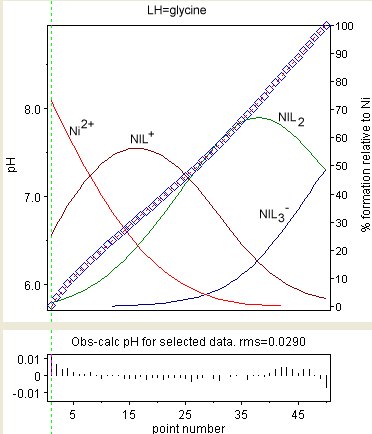
오른쪽의 도표는 Ni(⁺글리), Ni(글리),₂ Ni(글리), Ni(글리)⁻
₃의 안정성 상수(글리시 = 글리신)의 정제 결과를 나타낸다. 관찰된 값은 푸른 다이아몬드로 표시되고 종들의 농도는 총 니켈의 백분율로 중첩된다. 잔차가 아래 상자에 표시된다. 잔차는 예상한 대로 랜덤하게 분포되지 않는다. 이는 유리/액체 인터페이스에서의 액체 접합 전위 및 기타 효과의 변화 때문이다. 그러한 영향은 평형이 확립되는 속도에 비해 매우 느리다.

물리적 제약조건

일부 물리적 제약조건은 일반적으로 계산에 통합된다. 예를 들어 자유반응제 및 종의 모든 농도는 양의 값을 가져야 하며 연관 상수는 양의 값을 가져야 한다.

분광학 데이터의 경우 계산된 어금니 흡수성(또는 방출성) 값은 모두 양수여야 한다. 대부분의 컴퓨터 프로그램은 계산에 이런 제약을 가하지 않는다.

화학적 제약

금속-리간드 복합체의 안정성 상수를 결정할 때, 리간드 양성 상수를 금속이 없는 용액에서 얻은 데이터를 사용하여 결정된 값으로 고정하는 것이 일반적이다. 금속 이온의 가수 분해 상수는 보통 리간드가 없는 용액을 사용하여 얻은 값으로 고정된다. 3차 복합체 MAB의_pqr 안정성 상수를 결정할 때, 해당 이진 복합체 MA와_p′q′ MB의_{p′′q′′} 값을 개별 실험에서 결정한 값으로 고정하는 것이 일반적이다. 그러한 제약조건을 사용하면 결정되는 매개변수의 수가 감소하지만, 정제된 안정성 상수 값에 대한 계산된 오차가 과소 추정될 수 있다.

기타 모델

모형이 허용되지 않는 경우 실험 오차 내에서 실험 데이터에 가장 적합한 모형을 찾기 위해 다양한 다른 모형을 조사해야 한다. 가장 큰 어려움은 소위 소종이다. 이들은 농도가 매우 낮아 측정량에 미치는 영향이 실험 측정에서 오차 수준 이하인 종이다. 경미한 종에 대한 상수는 종의 농도를 증가시킬 수 있는 수단이 없는지를 판별하는 것이 불가능할 수도 있다.

구현

몇개의 간단한 시스템 스프레드 시트 계산에 다루기가 쉽죠.[4][9]

범용 컴퓨터 프로그램의 평형 상수 계산에 많은 출판되었다. 참고 문헌 목록에[10]를 참조하십시오. 가장 자주 사용하는 프로그램: 있다.

• Potentiometric 데이터: Hyperquad, BEST[11]PSEQUAD,[12]ReactLab pHPRO.
• Spectrophotometric 데이터:HypSpec, SQUAD,[12]Specfit,[13]ReactLab EQUILIBRIA.
• NMR데이터 HypNMR, EQNMR
• Calorimetric 데이터 HypΔH. Affinimeter
  상업 등온 적정 열량계 보통은 1:1부가물의 형성에 대한 평형과 표준 일정 형성 엔탈피 얻을 수 있는 소프트웨어와 함께 공급을 받고 있다. 더 복잡한 평형에 대처하는 일부 소프트웨어도 공급 받을 수 있다.

참조