디퍼렌셜 풀리

Differential pulley
디퍼렌셜 풀리의 예

차동 풀리(Weston differential pulley), 때로는 "차동 호이스트", "체인 호이스트" 또는 구어체로 "체인 낙하"라고도 함)는 자동차 엔진과 같은 매우 무거운 물체를 수동으로 들어 올리기 위해 사용됩니다.2개의 도르래를 공통 축으로 감싸고 있는 연속 체인의 느슨한 부분을 잡아당겨 작동한다.(2개의 도르래는 1개의 축에서 하나의 단위로 회전하도록 결합되어 있다.)연결된 두 풀리의 상대적 크기에 따라 손으로 들 수 있는 최대 중량이 결정됩니다.풀리 반경이 충분히 가까운 경우, 체인이 [1]당겨질 때까지 하중은 제자리(중력 하에서도 낮아지지 않음)를 유지합니다.

역사

차동 도르래는 1854년 영국 [2]킹스 노턴 출신의 토마스 알드리지 웨스턴에 의해 발명되었다.

도르래는 Richard와 George Tangye와 협력하여 제작되었습니다.리처드 탕예의 자서전에 따르면 웨스턴 차동 도르래는 중국의 차동 도르래에서 발전하여 유한한 길이의 로프를 끝없는 체인으로 대체하였다.그는 많은 엔지니어링 회사들이 도르래가 돌면서 효과적으로 치아에서 체인을 분리하는 데 어려움을 인정했지만, 그의 회사는 이 문제를 해결할 "피치" 체인을 개발했다고 주장했다."특허 체인 가이드 포함 웨스턴 디퍼렌셜 풀리 블록"으로 판매된 이 풀리는 9개월 동안 3000세트가 판매되는 등 좋은 판매고를 올렸다.1862년 런던에서 열린 국제박람회에서 롱헤든웨이트(510kg)부터 롱톤(3,000kg)까지 5가지 크기로 전시돼 '오리지널 응용, 실용성, 성공'으로 메달을 받았다.

한 철물업자가 웨스턴의 특허 이전에 도르래가 30년 동안 사용되었다고 Tangyes에 이의를 제기했지만, 판사 William Page Wood는 Tangyes의 손을 들어줬는데,[3] 그 이유는 그 결합 메커니즘이 증거로 제시된 것과 상당히 달랐기 때문이다.

예일 록 회사는 [2]1876년에 특허권을 취득했다.

멍청한 도르래는 아주 큰 질량을 짧은 거리에서 들어올릴 수 있다.서로 부착되어 회전하는 서로 다른 반지름의 고정 풀리 2개, 하중을 지탱하는 단일 풀리 및 풀리 주위에 루프가 있는 끝없는 로프로 구성됩니다.미끄러짐을 방지하기 위해 로프는 보통 체인으로 교체되고 연결된 풀리는 스프로켓으로 교체됩니다.

단일 풀리를 운반하는 체인의 두 섹션은 연결된 풀리에 대해 상반된 토크를 가하므로 체인의 느슨한 부분을 당겨서 이러한 토크의 차이만 수동으로 보상하면 됩니다.이는 하중을 들어올리는 데 필요한 힘은 하중의 극히 일부에 불과하다는 기계적 이점을 가져옵니다.동시에 하중을 들어올리는 거리는 같은 인자가 당기는 체인 길이보다 작다.이 계수(기계적 이점 MA)는 연결된 풀리의 반지름 r과 R의 상대적 차이에 따라 달라집니다.

힘과 거리에 대한 영향은 양적으로 다음과 같습니다(그림 참조).

반지름의 차이를 매우 작게 만들 수 있으므로 이 풀리 시스템의 기계적 이점을 매우 크게 [4][5]만들 수 있습니다.반지름이 0인 극단적인 경우 MA는 무한대가 되므로 체인을 이동하기 위한 힘(마찰 제외)이 필요하지 않지만 체인을 이동해도 하중이 더 이상 상승하지 않습니다.

다른 극단에서는 r이 0일 때 시스템은 기계적 이점 2를 가진 단순한 총 태클이 됩니다.

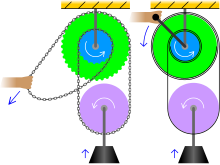
디퍼렌셜 풀리(왼쪽)와 디퍼렌셜 윈드글래스 또는 중국산 윈드글래스(오른쪽)의 비교.윈드글래스의 로프는 선명도를 위해 나선형으로 그려지지만, 이미지에 수직인 축이 있는 나선형일 가능성이 높다.

연결된 풀리가 윈치로 대체되는 디퍼렌셜 윈드글라스에서도 동일한 원리가 사용됩니다.

기계적 우위성의 계산

위 그림에서 체인의 4개 세그먼트는 W, X, Y 및 Z라는 라벨이 붙어 있습니다.대응하는 힘의 크기는 각각 F, FX, FY 및Z F입니다W.

체인이 무질량이라고 가정하면 세그먼트X X가 무게를 지지하지 않기 때문에 F = 0입니다.

시스템을 평형 상태로 취하면 F와WY F는 동일하며, 그렇지 않으면 하부 도르래가 자유자재로 회전합니다.

다음으로, 하부 풀리에 작용하는 아래쪽 힘은 풀리에 작용하는 위쪽 힘과 같기 때문에,

FL = FW + FY 또는 F = F이므로WY 2W F입니다.

또한 복합 풀리 주변에는 순 토크나 모멘트가 없으므로 시계 방향 토크는 반시계 방향 토크와 동일합니다.

FW R + FX r = FY r + FZ R 。

위의 방정식에서 F와Y F를 대입하면X,

FW R + 0 = FW R + FZ R 。

재배열로 제공

FW = FZ ·R/R - r.

FW = F /2로서

F/2 = FZ · R/R - r 。

마지막으로, 기계적 이점인 F/F = 2 R/R - r 또는 2/1 - r/R.

____________________________________________________________________________________________________________________________________________

크기가 다른 2개의 스프로킷의 체인 링크 포켓을 단순히 카운트하고 비교하는 것만으로 기계적 우위성을 계산하는 훨씬 간단한 방법을 실현할 수 있습니다.두 개의 스프로킷 P1(더 큰)과 P2(더 작은)의 포켓 수를 호출합니다.

부하를 들어 올릴 때, 이중 스프로킷 어셈블리가 완전히 회전할 때마다 P1 체인 링크 쌍(포켓 사이에 끼워지는 직각 링크)이 큰 스프로킷에 의해 채워지는 반면, P2 체인 링크 쌍은 작은 스프로킷에 의해 해제되어 P1-P2 체인 링크 쌍의 순 이득을 얻습니다.

기계적 우위성은 각 회전수에 필요한 체인 링크 쌍의 비율과 체인 링크 쌍의 순이익이 같아집니다.바꿔 말하면 기계적 이점은 각 단위 게인 거리에 필요한 당김 거리입니다.디퍼렌셜 스프로킷 쌍의 기계적 이점은 P1/(P1-P2)와 동일합니다.

부하에 이동 중인 풀리가 있기 때문에 고정(앵커링) 스프로킷 어셈블리의 기계적 이점이 두 배로 증가하여 총 2 x P1/(P1-P2)의 기계적 이점을 얻을 수 있습니다.

예를 들어, 1톤의 디퍼렌셜 체인 낙하에는 15포켓과 14포켓의 스프로켓 세트가 있습니다.그러면 총 2 X 15/(15-14) 또는 30:1의 기계적 이점이 제공됩니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Macauley, David; Ardley, Neil (1998). The New Way Things Work. Boston, USA: Houghton Mifflin Company. p. 56. ISBN 0-395-93847-3.
  2. ^ a b "The history makers". Hoist Magazine. World Market Intelligence. 3 February 2003.
  3. ^ "Differential pulley block, large and small sheaves, 2 ton capacity, invented by T A Weston / made by Tangyes Ltd". Powerhouse Museum. Museum of Applied Arts & Sciences. Archived from the original on 2013-04-11. Retrieved 3 October 2021.{{cite web}}: CS1 유지보수: 부적합한 URL(링크)
  4. ^ Black, N. Henry; Davis, Harvey N. (1922). Practical physics, fundamental principles and applications to daily life (2nd ed.). New York: Macmillan. p. 39.
  5. ^ United States Bureau of Naval Personnel (1974). Basic machines and how they work. Dover Publications. pp. 10–15. ISBN 9780486217093.