이산 하틀리 변환
Discrete Hartley transform이산형 하틀리 변환(DHT)은 이산형 푸리에 변환(DFT)과 유사한 이산형 주기적 데이터의 푸리에 관련 변환으로 신호 처리 및 관련 분야에서 유사하게 응용된다.그것의 DFT와의 주요 차별점은 복잡한 숫자의 본질적인 관여 없이 실제 입력을 실제 출력으로 변환한다는 것이다.DFT가 연속 푸리에 변환(FT)의 이산 아날로그인 것처럼 DHT는 1942년 랄프 V. L. 하틀리가 도입한 연속 하틀리 변환(HT)의 이산 아날로그다.[1]
빠른 푸리에 변환(FFT)과 유사한 DHT에 대한 빠른 알고리즘이 있기 때문에, DHT는 원래[2] 1983년 Ronald N. Bracewell에 의해 데이터가 순수하게 실제인 일반적인 사례에서 보다 효율적인 계산 도구로 제안되었다.그러나 실제 입력 또는 출력에 대한 전문 FFT 알고리즘은 일반적으로 DHT에 대한 어떤 해당 알고리즘보다 약간 적은 조작으로 찾을 수 있다는 주장이 뒤따랐다.
정의
형식적으로 이산형 하틀리 변환은 선형, 반전성 함수 H: Rn → Rn (R은 실수의 집합을 의미한다)이다.N실수 x0, ..., x는N−1 공식에 따라 N실수 H0, ..., H로N−1 변환된다.
조합은 (z)+죄 (z) 정해{\displaystyle \cos(z)+\sin(z)}=2cos(z4π −){\displaystyle={\sqrt{2}}\cos \left(z-{\frac{\pi}{4}}\right)}는 가끔 표시된 cas(z),며 혼란과 cis(z))eiz = cos(z)+나는 sin(z), 또는 e−iz)cis(−z) 나타나는의 DFT 정의(제가 거기 있다.그상상의 단위).
DFT와 마찬가지로 변환 앞에 있는 전체 스케일 팩터와 사인 항의 부호는 관례에 따른 것이다.비록 이러한 관습들이 때때로 작가들마다 다르지만, 그것들은 변환의 본질적인 속성에 영향을 미치지 않는다.
특성.
변환은 N-by-N 매트릭스에 의한 벡터(x0, ...., xN−1)의 곱으로 해석될 수 있으므로 이산형 하틀리 변환은 선형 연산자다.행렬은 변위할 수 없다; H에서k x를n 회복할 수 있는 역변형은 단순히 H의k DHT에 1/N을 곱한 것이다.즉, DHT는 전체 척도계수까지 자체 역(부여)이다.
DHT는 DFT를 계산하는 데 사용될 수 있으며, 그 반대의 경우도 마찬가지다.실제 입력 x의n 경우 DFT 출력 X에는k 실제 부품(Hk + HN−k)/2와 가상 부품(HN−kk - H)/2가 있다.반대로 DHT는 x의n DFT에 1 + i를 곱한 다음 결과의 실제 부분을 취하는 것과 동등하다.
DFT와 마찬가지로, 길이 N인 벡터 z = (xn)와 y = (ynn) 두 벡터 x = (x)와 y = (y)의 주기적 콘볼루션 z는 DHT 이후 간단한 조작이 된다.특히 벡터 X, Y, Z가 각각 x, y, z의 DHT를 나타낸다고 가정하자.그런 다음 Z의 요소는 다음과 같다.
여기서 모든 벡터는 N(XN = X0, 등)으로 주기적이어야 한다.따라서, DFT가 복잡한 숫자의 점 곱하기(실제 부분과 가상 부분의 쌍)로 콘볼루션을 변환하는 것처럼, DHT는 콘볼루션을 실제 주파수 성분의 쌍의 단순한 조합으로 변환한다.그러면 역 DHT는 원하는 벡터 z를 산출한다.이러한 방식으로 DHT에 대한 빠른 알고리즘(아래 참조)은 콘볼루션에 대한 빠른 알고리즘을 산출한다.(이것은 DFT의 해당 절차보다 약간 비싸며, 아래 변환 비용은 포함하지 않는다. 위의 쌍방향 연산은 복합 곱셈의 6과 비교하여 8개의 실제 산술 연산을 요구하기 때문이다.이 카운트는 2로 나누기를 포함하지 않으며, 예를 들어 역 DHT의 1/N 정규화로 흡수될 수 있다.)
빠른 알고리즘
DFT와 마찬가지로 DHT 정의를 직접 평가하려면 O(N2) 산술 연산이 필요하다(Big O 표기법 참조).그러나 FFT와 유사한 빠른 알고리즘이 존재하지만, 동일한 결과를 오직 O(N 로그 N) 연산에서만 계산한다.거의 모든 FFT 알고리즘, 쿨리 알고리즘-원시 요인 투 위노그라드(1985)[3]에서 브루운(1993)까지 이산 하틀리 변환에 대한 직접적인 아날로그가 있다.[4] (그러나 QFT와 같은 좀 더 이국적인 FFT 알고리즘 중 몇 가지는 DHT의 맥락에서 아직 조사되지 않았다.)
특히 쿨리-의 DHT 아날로그는투키 알고리즘은 일반적으로 빠른 하틀리 변환(FHT) 알고리즘으로 알려져 있으며, 1984년 브레이스웰에 의해 처음 설명되었다.[5]이 FHT 알고리즘은 적어도 N 사이즈의 파워-of-size에 적용될 때, 1987년에 스탠포드 대학에 발행된 미국 특허 번호 4,646,256의 대상이다.스탠포드는 1994년에 이 특허를 공공영역에 넣었다(Bracewell, 1995).[6]
위에서 언급한 바와 같이 DHT 알고리즘은 실제 입력(또는 출력)에 특화된 해당 DFT 알고리즘(FFFT)보다 일반적으로 (부동점 연산 수로 볼 때) 약간 덜 효율적이다.이것은 소렌센 외 연구진(1987년)[7]과 뒤하멜 & 베테르리(1987년)에 의해 처음 주장되었다.[8]후자의 저자들은 길이 N의 DHT를 길이 N/2의 DHT와 길이 N/4의 DHT(DHT가 아닌 실제 투입 DFT)로 분해하는 분할 레이더 알고리즘(스플릿-라디 FFT와 유사함)을 채택하여 2개의 크기 중 DHT에 대해 가장 낮은 것으로 보이는 운영 카운트를 얻었다.이러한 방식으로, 그들은 길이가 두 개인 DHT는 실투입 DFT에 해당하는 산술 연산의 개수보다 기껏해야 두 개가 더 추가되어 계산될 수 있다고 주장했다.
오늘날의 컴퓨터에서는 성능이 엄격한 연산수보다 캐시 및 CPU 파이프라인 고려사항에 의해 결정되며, 약간의 산술 비용 차이는 크지 않을 것으로 보인다.FHT와 Real-input FFT 알고리즘은 유사한 계산 구조를 가지므로, 둘 다 상당한 선행 속도 이점을 가지고 있지 않은 것으로 보인다(포포비치[와 셰비치, 1994).[9]실무적으로, 고도로 최적화된 실시간 입력 FFT 라이브러리는 많은 소스(예: Intel과 같은 CPU 벤더)에서 이용할 수 있는 반면, 고도로 최적화된 DHT 라이브러리는 덜 흔하다.
반면에 실제 입력에 의한 FFT의 중복 계산은 그러한 경우에 대한 O(N 로그 N) 복합 데이터 알고리즘이 존재함에도 불구하고 그러한 알고리즘의 복잡한 순열 및/또는 위상 회전 뒤에 이중화가 숨겨지기 때문에 대형 원시 N의 경우 제거하기가 더 어렵다.이와는 대조적으로, 표준 프라임 사이즈 FFT 알고리즘인 Rader's 알고리즘은 등가 복합 FFT의 그것보다 대략 두 개의 적은 계산에 대해 실제 데이터의 DHT에 직접 적용할 수 있다(Frigo and Johnson, 2005).[10]한편, Real-input DFT에 대한 Rader의 알고리즘의 비 DHT 기반 적응도 가능하다(Chu & Burrus, 1982년).[11]
다차원 이산하틀리 변환(MD-DHT)
rD-DHT("r" 치수가 있는 MD-DHT)는 다음을 통해 제공된다.
= , i - }- 여기서 (x)는 x )+ sin {이다.
1-D 사례와 유사하게, 실제적이고 대칭적인 변환으로서 MD-DHT는 MD-DFT보다 간단하다.첫 번째의 경우, 역 DHT는 스케일링 계수가 추가된 전방 변환과 동일하다.
둘째, 커널은 실제적이기 때문에 복잡한 숫자의 계산 복잡성을 피한다.또한 DFT는 간단한 부가 연산을 통해 DHT로부터 직접 얻을 수 있다(Bracewell, 1983).[2]
MD-DHT는 영상 및 광학 신호 처리와 같은 분야에서 널리 사용된다.특정 애플리케이션에는 컴퓨터 비전, 고화질 텔레비전, 원격 회의, 모션 이미지를 처리하거나 분석하는 영역(Zeng, 2000)이 포함된다.[12]
MD-DHT를 위한 빠른 알고리즘
컴퓨팅 속도가 계속 증가함에 따라, 더 큰 다차원적 문제들은 계산적으로 실현 가능하게 되어 빠른 다차원 알고리즘의 필요성이 요구되고 있다.그러한 세 가지 알고리즘이 뒤따른다.
효율성에 대한 분리 가능성을 추구하기 위해, 우리는 다음과 같은 변환을 고려한다(Bracewell, 1983).[2]
보르트펠트(1995년)[13]에서 두 사람이 몇 가지 추가에 의해 연관될 수 있다는 것을 보여주었다.예를 들어, 3-D에서는
의 경우 행-열 알고리즘을 구현할 수 있다이 기법은 그러한 R-C 알고리즘의 단순성 때문에 일반적으로 사용되지만 일반적인 M-D 공간에 최적화되어 있지는 않다.
radix-2, radix-4, split radix와 같은 다른 빠른 알고리즘이 개발되었다.예를 들어, Boussakta(2000년)[14]는 3-D 벡터 레이디스를 개발했다.
또한 이 3D 벡터 레이더 알고리즘이(4 ) 로그 2 N{\을 취한다는 것이 Boussakta(2000)[14]에서도 제시되었다. 곱하기 및( ) 3 N 승수와 2 ) 3 nN + 2{\2}})와 하여 N}N . 행-열 접근방식의 추가.단점은 이러한 라딕스 유형의 알고리즘 구현이 임의 치수의 신호에 대해 일반화하기 어렵다는 점이다.
숫자 이론 변환은 매우 빠른 경련을 일으키기 때문에 MD-DHT를 해결하는 데도 사용되어 왔다.부삭타(1988)에서는 MD-DHT 변환을 경련으로 구성된 형태로 분해하는 방법을 보여 주었다.[15]
2-D 사례의 경우(3-D 사례도 명시된 참조에서 다룬다)
,
다음과 같이 1-D 및 2-D 원형 경련으로 분해할 수 있다.
어디에
을(를) 추가로 개발하면서
이 시점에서 FNT(Fermat number transform)를 제시한다.tth Fermat 번호는 = + 에 의해, = 2 t {\t잘 알려진 페르마트 숫자는 = , 2,,,, (0 1, 2, 3, 4, 5, 6 (0,\,3 에 대한 이다).[15]Fermat 번호 변환은 다음에 의해 주어진다.
with . and are roots of unity of order and respectively 스타일alpha }=\{2}^{
분해로 돌아가면 , ) 의 마지막 용어는 X , l) 그 다음으로 표시된다.
및 }}이 N 과({\ 과( }이 프라임일 경우 존재함을 보장함)의 원시 라면 g {\ map to So, mapping and to and 2 다음과 같은 것을 얻는다.
= , -
그것은 이제 순환적인 경합이다.With , , and 1개:
여기서 은 용어 곱셈을 기준으로 용어를 나타낸다.또한 (Boussakta, 1988)[15]에서는 이 알고리즘이 다른 DHT 알고리즘에 비해 8~20배수의 배율을 감소시키는 것으로, 배율보다 단순하다고 가정하는 시프트 및 추가 운용 횟수가 약간 증가하는 비용을 들였다.이 알고리즘의 단점은 변환의 각 차원이 원시적 루트를 갖는 제약조건이다.
참조
- ^ Hartley, Ralph V. L. (March 1942). "A More Symmetrical Fourier Analysis Applied to Transmission Problems". Proceedings of the IRE. 30 (3): 144–150. doi:10.1109/JRPROC.1942.234333.
- ^ a b c Bracewell, Ronald N. (1983). "Discrete Hartley Transform". Journal of the Optical Society of America. 73 (12): 1832–1835. doi:10.1364/josa.73.001832.
- ^ Sorensen, Henrik V.; Jones, Douglas L.; Burrus, Charles Sidney; Heideman, Michael T. (1985). "On computing the discrete Hartley transform". IEEE Transactions on Acoustics, Speech, and Signal Processing. ASSP-33 (4): 1231–1238.
- ^ Bini, Dario Andrea; Bozzo, Enrico (1993). "Fast discrete transform by means of eigenpolynomials". Computers & Mathematics with Applications. 26 (9): 35–52. doi:10.1016/0898-1221(93)90004-f.
- ^ Bracewell, Ronald N. (1984). "The Fast Hartley Transform". Proceedings of the IEEE. 72 (8): 1010–1018. doi:10.1109/proc.1984.12968.
- ^ Bracewell, Ronald N. (1995). "Computing with the Hartley Transform". Computers in Physics. 9 (4): 373–379. Bibcode:1995ComPh...9..373B. doi:10.1063/1.168534.
- ^ Sorensen, Henrik V.; Jones, Douglas L.; Heideman, Michael T.; Burrus, Charles Sidney (1987). "Real-valued fast Fourier transform algorithms". IEEE Transactions on Acoustics, Speech, and Signal Processing. ASSP-35 (6): 849–863.
- ^ Duhamel, Pierre; Vetterli, Martin (1987). "Improved Fourier and Hartley transform algorithms: application to cyclic convolution of real data". IEEE Transactions on Acoustics, Speech, and Signal Processing. ASSP-35: 818–824.
- ^ Поповић [Popović], Миодраг [Miodrag]; Šević, Dragutin (1994). "A new look at the comparison of the fast Hartley and Fourier transforms". IEEE Transactions on Signal Processing. 42 (8): 2178–2182. Bibcode:1994ITSP...42.2178P. doi:10.1109/78.301854.
- ^ Frigo, Matteo; Johnson, Steven G. (2005). "The Design and Implementation of FFTW3" (PDF). Proceedings of the IEEE. 93 (2): 216–231. CiteSeerX 10.1.1.66.3097. doi:10.1109/jproc.2004.840301.}
- ^ Chu, Shuni; Burrus, Charles Sidney (1982). "A prime factor FTT [sic] algorithm using distributed arithmetic". IEEE Transactions on Acoustics, Speech, and Signal Processing. 30 (2): 217–227. doi:10.1109/tassp.1982.1163875.
- ^ Zeng, Yonghang; Bi, Guoan; Leyman, Abdul Rahim (2000). "Polynomial Transform Algorithms for Multidimensional Discrete Hartley Transform". IEEE International Symposium on Circuits and Systems (V): 517–520.
- ^ Bortfeld, Thomas; Dinter, Wolfgang (1995). "Calculation of Multidimensional Hartley Transforms Using One-Dimensional Fourier Transforms". IEEE Transactions on Signal Processing. 43 (5): 1306–1310. Bibcode:1995ITSP...43.1306B. doi:10.1109/78.382424.
- ^ a b Boussakta, Said; Alshibami, Osama (2000). "Fast Algorithm for the 3-D Discrete Hartley Transform". International Conference on Acoustics, Speech, and Signal Processing '00 (4): 2302–2305.
- ^ a b c Boussakta, Said; Holt, Alan G. J. (1988). "Fast Multidimensional Discrete Hartley Transform using Fermat Number Transform". IEE Proceedings G - Electronic Circuits and Systems. 135 (6): 235–237. doi:10.1049/ip-g-1.1988.0036.
추가 읽기
- Bracewell, Ronald N. (1986). The Hartley Transform (1 ed.). Oxford University Press. ISBN 978-0-19503969-6.
- Boussakta, Said; Holt, Alan G. J. (1988). "Fast Multidimensional Discrete Hartley Transform using Fermat Number Transform". IEE Proceedings G - Electronic Circuits and Systems. 135 (6): 235–237. doi:10.1049/ip-g-1.1988.0036.
- Hong, Jonathan; Vetterli, Martin; Duhamel, Pierre (1994). "Basefield transforms with the convolution property" (PDF). Proceedings of the IEEE. 82 (3): 400–412. doi:10.1109/5.272145.
- O'Neill, Mark A. (1988). "Faster than Fast Fourier". BYTE. 13 (4): 293–300.
- Olnejniczak, Kraig J.; Heydt, Gerald T. (March 1994). "Scanning the Special Section on the Hartley transform". Proceedings of the IEEE. 82: 372–380. (NB. 광범위한 서지학 포함)
![{\displaystyle H_{k}=\sum _{n=0}^{N-1}x_{n}\operatorname {cas} \left({\frac {2\pi }{N}}nk\right)=\sum _{n=0}^{N-1}x_{n}\left[\cos \left({\frac {2\pi }{N}}nk\right)+\sin \left({\frac {2\pi }{N}}nk\right)\right]\quad \quad k=0,\dots ,N-1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73ba8d036230283b86eb38c9e498e214973d0a0d)
![{\begin{matrix}Z_{k}&=&\left[X_{k}\left(Y_{k}+Y_{{N-k}}\right)+X_{{N-k}}\left(Y_{k}-Y_{{N-k}}\right)\right]/2\\Z_{{N-k}}&=&\left[X_{{N-k}}\left(Y_{k}+Y_{{N-k}}\right)-X_{k}\left(Y_{k}-Y_{{N-k}}\right)\right]/2\end{matrix}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4fae2de8d1caaf64f2b6e5e1a877133bebe6a39)



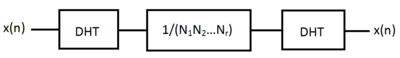

![{\displaystyle X(k_{1},k_{2},k_{3})={\frac {1}{2}}[{\hat {X}}(k_{1},k_{2},-k_{3})+{\hat {X}}(k_{1},-k_{2},k_{3})+{\hat {X}}(-k_{1},k_{2},k_{3})-{\hat {X}}(-k_{1},-k_{2},-k_{3})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee7357fed5235398b385ba6cb3b68e9a073e5704)


















 (를) 추가로 개발하면서
(를) 추가로 개발하면서





 대한
대한 
























![{\displaystyle Y(k,l)=FNT^{-1}\{FNT[y(n,m)]\otimes FNT[h(n,m)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eebe41901610887e540c58bc1d96b810eb607165)