거리 기하학

거리 기하학은 멤버 쌍 사이의 거리에 대한 주어진 값만을 기초로 한 점 집합의 특성화 및 연구다.^[1][2][3] 좀 더 추상적으로, 그것은 반모양 공간과 그 사이의 등축 변환에 대한 학문이다. 이 관점에서는, 일반 위상 내에서 주체로 간주할 수 있다.^[4]

역사적으로 거리 기하학의 첫 번째 결과는 AD 1세기 헤론의 공식이다. 현대 이론은 19세기에 아서 케일리의 연구로 시작되었고, 20세기에 칼 멩거 등의 보다 광범위한 발전이 뒤따랐다.

거리 기하학 문제는 생물학,^[4] 센서 네트워크,^[5] 측량, 항법, 지도학, 물리학과 같이 지점들 사이의 거리로부터 점들의 구성(상대 위치)의 형태를 유추할 필요가 있을 때마다 발생한다.

소개 및 정의

거리 기하학의 개념은 우선 두 가지 특정한 문제를 설명함으로써 설명될 것이다.

첫 번째 문제: 쌍곡선 탐색

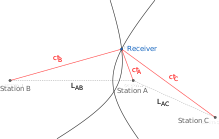
위치가 알려진 지상 라디오 방송국 A, B, C 3곳을 고려해 보십시오. 무선 수신기가 알 수 없는 위치에 있다. The times it takes for a radio signal to travel from the stations to the receiver, ${\displaystyle t_{A},t_{B},t_{C}}$, are unknown, but the time differences, ${\displaystyle t_{A}-t_{B}}$ and ${\displaystyle t_{A}-t_{C}}$, are known. 이들로부터 $c{\displaystyle ({}_{}}$ ${\displaystyle A_{}}$- t $){\displaystyle c(t_{A}-t_{B}}})$와 c${\displaystyle (t_{}}$ -${\displaystyle {}_{}{}_{}}$ ${\displaystyle C_{}}$)${\displaystyle c(t_{A}-t_{C})$의 거리 차이를 알 수 있으며$,$ 여기서 수신기의 위치를 찾을 수 있다.

두 번째 문제: 치수 축소

데이터 분석에서 벡터 $v{\displaystyle \mathbf{}}$=${\displaystyle }$( ${\displaystyle {x\mathrm{}}_{}}$ 1${\displaystyle }$,${\displaystyle }$… , ${\displaystyle {}_{}{n}_{}}$ )${\displaystyle }$∈ R ${\displaystyle {}^{}}$ ${\\$ =($x_{1},\ldots, x_{n}})$로 표현되는 데이터 목록이 종종 주어지며, $\mathb {R}$^{$n$에서 그것들이 저차원 아핀 하위 공간 내에 존재하는지 여부를 확인할 필요가 있다. 저차원적인 데이터 표현은 저장 공간 절약, 연산 시간 단축, 데이터에 대한 더 나은 통찰력 제공 등 많은 장점이 있다.

정의들

이제 우리는 우리의 문제를 고려하면서 자연스럽게 생기는 몇 가지 정의를 공식화한다.

반모양 공간

Given a list of points on ${\displaystyle R=\{P_{0},\ldots ,P_{n}\}}$, ${\displaystyle n\geq 0}$, we can arbitrarily specify the distances between pairs of points by a list of ${\displaystyle d_{ij}>0}$, ${\displaystyle 0\leq i<j\leq n}$. 이것은 삼각형 불평등이 없는 미터법 공간인 준측정학적 공간을 정의한다.

명시적으로, 세미메트릭 공간을 $세미메트릭$ $d{\displaystyle }$: ${\displaystyle R}$$$${\displaystyle \times }$ ${\displaystyle \mathrm{R}}$→${\displaystyle }$[ 0 ,${\displaystyle \mathrm{\infty }}$) ${\displaystyle d:$$R{\displaystyle }$$\time R\to [0,\fty )}$ 이렇게$$ 모든 x에 대해 ${\displaystyle y\in }$ R ${\displaystyle$ x$,y\in$ R$\},$

1. $긍정성{\displaystyle }$: d${\displaystyle }$( ${\displaystyle x}$, ${\displaystyle y}$)${\displaystyle }$= 0 ${\displaystyle d(x,y)=0}$인 경우에만$,$ ${\displaystyle x}$= y ${\displaystyle$ x$=y}$ .
2. 대칭: $d{\displaystyle }$( ${\displaystyle x}$, ${\displaystyle y}$)${\displaystyle }$= ${\displaystyle d}$( y${\displaystyle }$, ${\displaystyle x}$) ${\displaystyle d(x,y)=d(y,x)}$.

모든 미터법 공간은 반모양 공간이다. 특히 $R{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$ $k{\displaystyle }$ ${\displaystyle k}$ -차원$$ 유클리드 공간은 거리 기하학에서 표준 미터법 공간이다.

삼각형 불평등은 정의에서 생략되는데, $왜냐하면{\displaystyle {}_{}}$ 우리는 d ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$ 거리에 그것들이 양성이라는 단순한 요건보다$$ 더 많은 제약조건을 강요하고 싶지 않기 때문이다.

실제로 반모수 공간은 부정확한 측정으로 인해 자연스레 발생한다. ${\displaystyle {예}_{}}$를 들어, 선에$$ 점${\displaystyle }A{\displaystyle }$, ${\displaystyle B,}$ ${\displaystyle C}${\$displaystyle A,B,C}$이(가) 세 개 주어지며,${\displaystyle {}_{}}$d${\displaystyle {}_{}{A}_{}}$ ${\displaystyle \mathrm{B}}$ = 1,${\displaystyle {}_{}}$ ${\displaystyle B_{}{}_{}}$= ${\displaystyle 1}$,${\displaystyle {}_{}}$ A = 2 {\$displaystyle d_{$$AB}=1,d_{$$BC}=1,d_{$$AC}=2$ 부정확한 측정이 $d{\displaystyle {}_{}}$ ${\displaystyle A_{}}$ ${\displaystyle B_{}}$= 0${\displaystyle .99,}$ ${\displaystyle {}_{}}$ ${\displaystyle B_{}}$ ${\displaystyle C_{}}$= ${\displaystyle 0.98,}$ ${\displaystyle {}_{}}$ ${\displaystyle A_{}}$ ${\displaystyle C_{}}$=${\displaystyle 2.00}$ ${\displaystyle d_{$을 제공할 수 있음$AB}=0.99,d_{$$BC}=0.98,d_{$$AC}=2.00},$ 삼각형 불평등 위반$.$

등축 임베딩

$({\displaystyle }$R ,${\displaystyle d}$)${\displaystyle }$,${\displaystyle }$( ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$, ( ${\displaystyle {}^{}}$ ${\displaystyle )}$ , d ${\displaystyle {\prime }^{}}$ ) ${\displaystyle (R,d),(R',d')}$의 두 개의 반모수적 공간이 주어진 $경우{\displaystyle }$$,$ R$${\$displaystyle R$}에서 R${\displaystyle {}^{}}${$${\$displaystystyle$ $R}$까지 등축 포함은 지도$$ $f{\displaystyle }$: R${\displaystyle }$→ ${\displaystyle {}^{}}$ → R ${\displaystyle {\prime }^{}}$ ${\$모든 $x{\displaystyle }$, ${\displaystyle y}$ ${\displaystyle \in }$ ${\displaystyle R}$ ${\displaystyle$ x$,y\in R}$, $d{\displaystyle }$( x${\displaystyle }$, ${\displaystyle y}$)${\displaystyle }$= ${\displaystyle d}$ ${\displaystyle {\prime }^{}}$( f${\displaystyle }$( ${\displaystyle x}$)${\displaystyle }$, ${\displaystyle f}$( y${\displaystyle }$)${\displaystyle$d($x,y)=d$'($f(x),f(y)}$을 보존하는$$ $R\to R$$\text{'}\}.$

For example, given the finite semimetric space ${\displaystyle (R,d)}$ defined above, an isometric embedding into is defined by points ${\textstyle A_{0},A_{1},\ldots ,A_{n}\in \mathbb {R} ^{k}}$, such that ${\displaystyle d(A_{i},$$A_{j}=d_{ij}$ 모든 < $>[\displaystyle 0\leq i<j\leq n}$.

아핀 독립

iff 그들은 Rkm그리고 4.9초 만{\displaystyle \mathbb{R}^{k}의 단일 나는{나는\displaystyle}-dimensional 관계 부분 공간 안으로 들어갈 수 없는 지점 A0A1,…, ∈ Rk{\textstyle A_{0},A_{1},\ldots\mathbb{R}^{k},A_{n}\in n}그들은 affinely 독립적이 되도록}, 어떤ℓ<>;n{\disp 정의되어 있다.놓다$스타일{\displaystyle }$ $\ell <n$$},$ 만일 n {\$displaystyle n}$ -simplex$$ 이 범위, ${\displaystyle v_{}}$ $n{\displaystyle {}_{}}$ ${\$은$($는 양의 $n{\displaystyle }$ ${\displaystyle n$ $-volume$, >0 ${\style$\operatorname ${n} _${n}($v_{n$})을$({$n

일반적으로 $k{\displaystyle }$≥${\displaystyle n}$ ${\displaystyle k\geq n}$이$($가) 있을 때 일반 n-심플렉스(n-simplex)는 비감소성이기 때문에 그들은 친절하게 독립적이다. 예를 들어, 평면의 3개 점은 일반적으로 선분할로 변질되지 않기 때문에 선분할이 되지 않는다. 마찬가지로, 일반적으로 우주에서 4개의 지점은 공동행렬이 아니다. 왜냐하면 그것들이 가로지르는 사면체는 평평한 삼각형으로 변질되지 않기 때문이다.

> ${\displaystyle n>k}$일때, 그들은 친절하게 의존해야 한다. 이는 ${\displaystyle {}^{}}$ ${\$ 안에 들어갈 수 있는 $n{\displaystyle }$ ${\displaystyle n}$ -simplex는$$ 모두 "평평평한"이어야$$ 함을 참고하여 확인할 수 있다.

케이리-멘거 결정 요인

아서 케일리와 칼 멩거의 이름을 딴 케이리-멩거 결정요인은 점 집합 사이의 거리 행렬의 결정요인이다.

A ${0\mathrm{}}_{}$ ${}_{}$ ${1\mathrm{}}_{}$,$\dots ,$ $n_{}$ ${\$을(를) 반모양 공간에서 n + 1 포인트로$$ 두십시오. 이들의 Cayley-Menger 결정 인수는 다음과 같이 정의된다.

${\displaystyle \operatorname{CM}(A_{0}일 경우 ,\cdots ,A_{n})={\begin{vmatrix}0&, d_{01}^{2}&, d_{02}^{2}&, \cdots &, d_{중·소도시 택지 공급 사업}^{2}&, 1\\d_{01}^{2}&, 0&, d_{12}^{2}&, \cdots &, d_{1n}^{2}&, 1\\d_{02}^{2}&, d_{12}^{2}&, 0&, \cdots &, d_{2n}^{2}&, 1\\\vdots, \vdots, \vdots & &, \ddots & &, \vdots &, \vdots \\d_{중·소도시 택지 공급 사업}^{2}&.앰프, d_{1n}^{2}&, d_{2n}^{2}&, \cdots &, 0&, 1\\1&, 1&, 1&, \cdots &, 1&, 0\end{vmatrix}}}$

A0A1,…, An∈ Rk{\textstyle A_{0},A_{1},\ldots}, 그 때 그들은}Rkm그리고 4.9초 만{\displaystyle \mathbb{R}^{k}에}( 어쩌면 타락하다.)n-simplex vn{\displaystyle v_{n}의 vertices를 차지하고 있다. 그것은 보여 줄 수 있\mathbb{R}^{k},A_{n}\in that[6]은 심플렉스 v의 다차원 볼륨 n.${\displaystyle v_{n}$ 충족$$

${\displaystyle \operatorname {Vol} _{n}(v_{n})^{2}={\frac {(-1)^{n+1}:{n+1}{(n!)^{2}2^{n}}}\operatorname {CM}(A_{0},\ldots,A_{n}).}$

$n{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle n=0}$의 경우$$${\displaystyle {\mathrm{Vol}}_{}}$ ${\displaystyle {0\mathrm{}}_{}(\mathrm{v}{}_{}}$)${\displaystyle }$= 1 ${\displaystyle \operatorname {Vol} _{0}(v_{0}}=1})$이 있으며, 이는$$0-simplex의 "0차원 볼륨"이 1이라는 의미입니다.

A0A1,…, An{\textstyle A_{0},A_{1},\ldots ,A_{n}}은 affinely 독립 iff권 n⁡(vn)>0{\displaystyle \operatorname{권}_ᆲ(v_{n})>. 0}일 경우, 그것은,(− 1)n+1CM(A0,…, An)을 ⁡;0{\displaystyle())^{n+1}\operatorname{CM}(A_{0}일 경우 ,\ldots ,A_{n})>0}.따라서 Cayley–Men발아 결정요소는 확실한 독립성을 증명할 수 있는 계산적 방법을 제공한다.

만약 k <, n{\displaystyle k<, n}, 다음 포인트 affinely 의존하야 한다 CM⁡ 그것은=0((A_{0}일 경우 ,\ldots ,A_{n})=0}. 케일리의 1841년 종이 컵 k의 특별한 케이스 3, nx4{\displaystyle k=3,n=4}, 어떠한 5지점 A0,…, A4{\disp(A0,…, An).laysty3차원 공간의$$ $le A_{0},\ldots, A_{4$${\displaystyle {}_{}}$는 ${\displaystyle \mathrm{CM}}$⁡${\displaystyle }$(${\displaystyle {A\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$,${\displaystyle }$… ,${\displaystyle {}_{}}$) = ${\displaystyle 0}$ ${\displaystyle \operatorname {CM}(A_{0},\ldots ,A_{4}=0})$이 있어야 한다$.$

역사

거리 기하학의 첫 번째 결과는 AD 1세기부터 헤론의 공식으로, 3개의 꼭지점 사이의 거리에서 삼각형의 면적을 제공한다. AD 7세기부터 브라만구파의 공식은 그것을 주기적인 4차 측정법으로 일반화한다. AD 16세기부터 타르타글리아는 4정점 사이의 거리에서 4면체의 부피를 주기 위해 그것을 일반화했다.

현대적인 거리 기하학의 이론은 Authur Cayley와 Karl Menger로부터 시작되었다.^[7] Cayley는 1841년에 Cayley 결정인자를 발표했는데,^[8] 이것은 일반 Cayley-Menger 결정인자의 특별한 경우다. Menger는 1928년에 N-차원 유클리드 ${\displaystyle {}^{}}$ R n ${\$ ^{$n}}$에 등축 가능한 모든 반모수 공간의 특성화 정리를 증명하였다$.$^[9][10] 1931년에 Menger는 거리 관계를 이용하여 유클리드 기하학의 공리적인 처리를 하였다.^[11]

레오나드 블루멘탈의 책은^[12] 대학원 수준의 거리 기하학에 대한 전반적인 개요를 제시하는데, 이 중 상당 부분이 출간 당시 처음으로 영어로 다뤄진다.

멘거 특성화 정리

멩거는 반모양 공간의 다음과 같은 특성화 정리를 증명했다.^[2]

A semimetric space ${\displaystyle (R,d)}$ is isometrically embeddable in the ${\displaystyle n}$-dimensional Euclidean space ${\displaystyle \mathbb {R} ^{n}}$, but not in ${\displaystyle \mathbb {R} ^{m}}$ for any ${\displaystyle 0\leq m<n}$, if and only if:

1. ${\displaystyle R}$ ${\displaystyle R}$은(는) $({\displaystyle \mathrm{n}}$+ ${\displaystyle 1}$${\displaystyle }$${\displaystyle )}$ ${\$$displaystyle$($n$$+1)}$ -등각도$$ 부분 집합 $S{\displaystyle }$ ${\$$displaystyle$$S}$을(를$)$ 포함하며$,{\displaystyle }$ R ${\displaystyle {}^{}}$ ${\$^{$n}$; ;
2. any ${\displaystyle (n+3)}$-point subset ${\displaystyle S'}$, obtained by adding any two additional points of ${\displaystyle R}$ to ${\displaystyle S}$, is congruent to an ${\displaystyle (n+3)}$-point subset of ${\displaystyle \mathbb {R} ^{n}}$.

약간 약해진 형태의 이 정리의 증명(반모수 공간 대신 미터 공간)이 들어 있다.^[13]

Cayley-Menger 결정요인을 통한 특성화

블루메탈의 저서에서 다음과 같은 결과가 증명된다.^[12]

$R{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$에 ${\displaystyle \mathrm{n}}$+ 1 ${\displaystyle n+1}$ 포인트$$ 포함

S와 같이{20,…, Pn}{\displaystyle S=\{P_{0},\ldots ,P_{n}\}}, d(P나는, Pj))semimetric 공간(S, d){\displaystyle(S,d)}을 감안할 때 나는 ≥ 0{\displaystyle d(P_{나는},P_{j})=d_{ij}\geq 0}일 경우, 0i< ≤, j dj≤ n{\displaystyle 0\leq i<,j\leq n}, 등거맀던 1가지 이슈 때문이었습니다의(S, d ){)$displaystyle (S,d)}$ into ${\displaystyle \mathbb {R} ^{n}}$ is defined by ${\textstyle A_{0},A_{1},\ldots ,A_{n}\in \mathbb {R} ^{n}}$, such that ${\displaystyle d(A_{i},$$A_{j}=d_{ij}$ 모든 < $>[\displaystyle 0\leq i<j\leq n}$.

다시 한번, 그러한 등축 임베딩이${\displaystyle }$(${\displaystyle S}$, ${\displaystyle d}$) ${\디스플레이$ 스타일 $(S,d)}$ 에 존재하는지 묻는다$.$

필요한 조건은 쉽게 볼 수 있다: ${\displaystyle {모든}_{}}$ ${\displaystyle k}$ ${\displaystyle =}$ ${\displaystyle 1}$,${\displaystyle }$…${\displaystyle }$, n ${\displaystyle k=1,\ldots ,n$에 대해 v $k{\displaystyle {}_{}}$ ${\$를 ${A\mathrm{}}_{}$ 0${}_{}$, ${}_{}$ ${1\mathrm{}}_{}$,$$, , , $K_{}$ ${\$에 의해 형성된 k-s.

${\displaystyle(-1)^{k+1}\operatorname {CM}(P_{0},\ldots,P_{k})=(1-1)^{k+1}\opername {CM}(A_{0},\ldots,A_{k}}=2^{k}(k!)^{k}\operatorname {Vol} _{k}(v_{k})^{2}\geq 0}$

그 반대의 경우도 마찬가지다. 즉, 모든 $k{\displaystyle }$= ${\displaystyle 1}$,${\displaystyle }$…${\displaystyle }$, ${\displaystyle n}$ ${\displaystyle k=1,\ldots,n$

${\displaystyle(-1)^{k+1}\operatorname {CM}(P_{0},\ldots,P_{k})\geq 0,}$

그런 임베딩이 존재한다는 거지

Further, such embedding is unique up to isometry in ${\displaystyle \mathbb {R} ^{n}}$. That is, given any two isometric embeddings defined by ${\textstyle A_{0},A_{1},\ldots ,A_{n}}$, and ${\textstyle A'_{0},A'_{1},\ldots ,A'_{n}}$, there exists a (not 필수적으로 고유함) 등계법 $T{\displaystyle }$: ${\displaystyle {}^{}}$ ${\displaystyle {}^{}{}^{}}$→ R ${\displaystyle {\mathbb{}}^{}}$ ${\$ T$:\mathb {R} ^{n}\to \mathb {R} ^{n$ $T{\displaystyle }$(${\displaystyle {}_{}}$ ${\displaystyle k_{}}$)${\displaystyle }$= ${\displaystyle {}_{}^{}}$ ${\displaystyle k_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$$A'_{k}}$ for all ${\displaystyle k=0,\ldots ,n}$. Such ${\displaystyle T}$ is unique if and only if ${\displaystyle \operatorname {CM} (P_{0},\ldots ,P_{n})\neq 0}$, that is, ${\textstyle A_{0},A_{1},\ldots ,A_{n}}$ are affinely independent.

$n{\displaystyle }$${\displaystyle }$+ ${\displaystyle 2}$ ${\displaystyle n+2}$ ${\displaystyle \mathrm{및<img\; alt="n+2"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/aaf4207e44c00a9312fe3e8710efbefcd6eafdc0"\; style="vertical-align:\; -0.505ex;\; width:5.398ex;\; height:2.343ex;">}}$ n${\displaystyle }$+ 3 ${\displaystyle n+3}$ 포인트$$ 포함

If ${\displaystyle n+2}$ points ${\displaystyle P_{0},\ldots ,P_{n+1}}$ can be embedded in ${\displaystyle \mathbb {R} ^{n}}$ as ${\displaystyle A_{0},\ldots ,A_{n+1}}$, then other than the conditions above, an additional necessary condition is that the $$${\displaystyle }$$($${\displaystyle n}$+ $){\displaystyle (n+1)}$ -A ${}_{}$,${}_{}{}_{}$ ${1\mathrm{}}_{}$,$\dots ,$ $n_{}$+ $1_{}$ ${\$$,$${n$${\displaystyle +}$$1$}에 의해 형성된 심플렉스에는${\displaystyle }$(${\displaystyle n}$+ 1 ) {\$displaystystyle (n+1)$-차원$$ 볼륨이 있어야 한다. 즉, ${\displaystyle \mathrm{CM}}$ ${\displaystyle }$(${\displaystyle {P\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$,${\displaystyle }$… ,${\displaystyle P_{}}$ ${\displaystyle {}_{}}$, ${\displaystyle P_{}}$ n${\displaystyle {}_{}}$+ ${\displaystyle 1_{}}$)${\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle \operatorname {CM}(P_{0},\ldots, P_{n}, P_{n+1}=0$

그 반대의 경우도 마찬가지다. 즉, 모든 $k{\displaystyle }$= ${\displaystyle 1}$,${\displaystyle }$…${\displaystyle }$, ${\displaystyle n}$ ${\displaystyle k=1,\ldots,n$

${\displaystyle(-1)^{k+1}\operatorname {CM}(P_{0},\ldots,P_{k})\geq 0,}$

그리고

${\displaystyle \operatorname {CM}(P_{0},\ldots ,P_{n},P_{n+1}=0,}$

그런 임베딩이 존재한다는 거지

${\displaystyle {}^{}}$ ${\$에 $n{\displaystyle }$+ ${\displaystyle 3}$ ${\displaystyle n+3}$ 포인트를 내장하는$$ 경우 필요한 조건과 충분한 조건이 유사하다$.$

1. ${\displaystyle \mathrm{모든}}$ $k{\displaystyle }$= ${\displaystyle 1}$,${\displaystyle }$…${\displaystyle }$, n ${\displaystyle k=1,\$${\displaystyle \mathrm{ldots}}$$,n}$,${\displaystyle }$(${\displaystyle }$- 1${\displaystyle {}^{}}$)${\displaystyle k^{}}$ + ${\displaystyle 1^{}}$ ${\displaystyle \mathrm{CM}}$ ${\displaystyle }$ ${\displaystyle ({P\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$,${\displaystyle }$,${\displaystyle }$, ${\displaystyle P_{}}$ )${\displaystyle 0}$ 0 ${\displaystyle(-1)^{k+1}\operatorname {CM}(P_{0$$ldots,P_{k}}})\geq 0}}$
2. ${\displaystyle \operatorname {CM}(P_{0},\ldots ,P_{n},P_{n+1}=0;}$
3. ${\displaystyle \operatorname {CM}(P_{0},\ldots ,P_{n},P_{n+2}=0;}$
4. ${\displaystyle \operatorname {CM}(P_{0},\ldots ,P_{n},P_{n+1},P_{n+2}=0.}$

임의로 많은 포인트 포함

$일반적$으로 n${\displaystyle }$+ ${\displaystyle 3}$ ${\displaystyle n+3}$ 사례가$$ 충분한 것으로 나타났다.

In general, given a semimetric space ${\displaystyle (R,d)}$, it can be isometrically embedded in ${\displaystyle \mathbb {R} ^{n}}$ if and only if there exists ${\displaystyle P_{0},\ldots ,P_{n}\in R}$, such that, for all ${\displaystyle k=1,\ldots ,n}$, ${\displaystyle (-1}$${\displaystyle (-1)^{k+1}\operatorname {CM} (P_{0},\ldots ,P_{k})\geq 0}$, and for any ${\displaystyle P_{n+1},P_{n+2}\in R}$,

1. ${\displaystyle \operatorname {CM}(P_{0},\ldots ,P_{n},P_{n+1}=0;}$
2. ${\displaystyle \operatorname {CM}(P_{0},\ldots ,P_{n},P_{n+2}=0;}$
3. ${\displaystyle \operatorname {CM}(P_{0},\ldots ,P_{n},P_{n+1},P_{n+2}=0.}$

그리고 그러한 임베딩은 ${\displaystyle {}^{}}$ ${\$에 있는 등소계까지 고유하다$.$

Further, if ${\displaystyle \operatorname {CM} (P_{0},\ldots ,P_{n})\neq 0}$, then it cannot be isometrically embedded in any ${\displaystyle \mathbb {R} ^{m},m<n}$. And such embedding is unique up to unique isometry in ${\displaystyle \mathbb {R} ^{n}}$.

따라서 Cayley-Menger 결정요인은 ${\displaystyle {}^{}}$한 $n{\displaystyle }$ ${\displaystyle$ $\$$mathb$${R}$$$^{$n}$에 반모수 공간을 삽입할 수 있는지, 그리고 만약 그렇다면 최소 $n{\displaystyle }$ ${\displaystyle n}$은 무엇인지 계산할 수 있는 구체적인 방법을 제공한다$.$

적용들

거리 기하학에는 많은 응용이 있다.^[3]

GPS와 같은 통신망에서는 일부 센서의 위치가 알려져 있고(앵커라고 불리며), 센서 간 거리도 일부 알려져 있는데, 문제는 모든 센서의 위치를 파악하는 것이다.^[5] 쌍곡선 항법술은 신호가 앵커에 도달하는 데 걸리는 시간을 기준으로 선박 위치 파악에 거리 형상을 이용하는 GPS 전 기술이다.

화학에는 많은 응용이 있다.^[4][12] NMR과 같은 기술은 주어진 분자의 원자 쌍 사이의 거리를 측정할 수 있는데 문제는 그 거리에서 분자의 3차원 형태를 유추하는 것이다.

애플리케이션용 소프트웨어 패키지:

• DGSOL. 고분자 모델링에서 장거리 기하학적 문제를 해결한다.
• Xplor-NIH. X-PLOR을 기반으로 NMR 실험의 데이터를 기반으로 분자의 구조를 결정한다. 그것은 (시뮬레이션 어닐링과 같은) 경험적 방법 및 국소적 검색 방법(결합 구배 최소화 등)으로 거리 기하학적 문제를 해결한다.
• 팅커. 분자 모델링과 디자인. 그것은 거리 기하학 문제를 해결할 수 있다.
• SNLSDPclique. 센서 간 거리를 기준으로 센서 네트워크에서 센서를 찾는 MATLAB 코드.

참고 항목

• 유클리드 거리 행렬
• 다차원 스케일링(임의의 오차로 거리를 측정할 때 사용되는 통계 기법)
• 미터법 공간
• 타르타글리아의 공식
• 삼각측량
• 삼각측량

참조