치수 축소

Dimensionality reduction
물리학의 치수 축소는 치수 축소를 참조하십시오.

차원 축소 또는 차원 축소는 데이터를 고차원 공간에서 저차원 공간으로 변환하는 것으로, 저차원 표현이 본래의 차원에 가까운 의미 있는 데이터를 유지하는 것이 이상적입니다.고차원 공간에서 작업하는 것은 여러 가지 이유로 바람직하지 않을 수 있습니다. 즉, 원시 데이터는 종종 차원성의 저주의 결과로 희박하며, 데이터 분석은 일반적으로 계산적으로 다루기 어렵습니다(제어 또는 처리하기가 어렵습니다).차원성 감소는 신호 처리, 음성 인식, 신경 정보학 및 생물 정보학 [1]등 다수의 관측치 및/또는 변수를 다루는 분야에서 일반적이다.

방법은 일반적으로 선형 [1]접근법과 비선형 접근법으로 나뉜다.접근법은 피쳐 선택과 피쳐 [2]추출로 나눌 수도 있습니다.차원 축소는 소음 감소, 데이터 시각화, 클러스터 분석 또는 다른 분석을 용이하게 하기 위한 중간 단계로 사용할 수 있다.

기능 선택

주요 기사:기능 선택
다음 항목도 참조하십시오.조합 최적화

피쳐 선택 접근법은 입력 변수의 서브셋(기능 또는 속성이라고도 함)을 찾으려고 합니다.세 가지 전략은 필터 전략(예: 정보 획득), 래퍼 전략(예: 정확도에 따라 검색) 및 임베디드 전략(예: 예측 오류를 기반으로 모델을 구축하는 동안 선택된 기능이 추가 또는 제거됨)입니다.

원래 [3]공간보다 축소된 공간에서 회귀나 분류와 같은 데이터 분석을 더 정확하게 수행할 수 있습니다.

특징 투영

주요 기사:기능 추출

피쳐 투영(피처 추출이라고도 함)은 데이터를 고차원 공간에서 더 적은 차원의 공간으로 변환합니다.데이터 변환은 주성분 분석(PCA)과 같이 선형적일 수 있지만 많은 비선형 차원 축소 기법도 존재합니다.[4][5]다차원 데이터의 경우, 텐서 표현은 다선형 부분 공간 [6]학습을 통한 차원 감소에 사용될 수 있다.

A scatterplot showing two groups points. An axis runs through the groups. They transition into a histogram showing where each point lands in the PCA projection.
2D 점 세트에 대한 결과 PCA 투영을 시각적으로 표현한 것입니다.

주성분분석(PCA)

주요 기사 : 주성분 분석

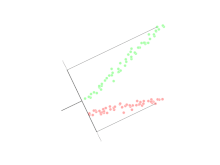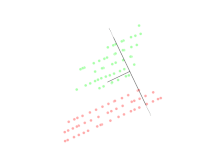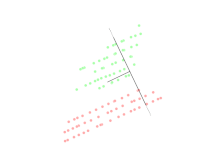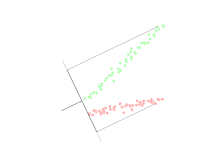
차원 축소를 위한 주요 선형 기술인 주성분 분석은 저차원 표현에서 데이터의 분산을 최대화하는 방식으로 저차원 공간에 대한 데이터의 선형 매핑을 수행합니다.실제로 데이터의 공분산 행렬(때로는 상관 관계)이 구성되고 이 행렬의 고유 벡터가 계산됩니다.이제 가장 큰 고유값(주성분)에 해당하는 고유 벡터를 사용하여 원래 데이터의 분산 중 큰 부분을 재구성할 수 있습니다.더욱이, 처음 몇 개의 고유 벡터는 종종 시스템의 대규모 물리적 동작의 관점에서 해석될 수 있다. 왜냐하면 그것들은 종종 특히 저차원 시스템에서 시스템 에너지의 대부분을 기여하기 때문이다.다만, 이 동작은, 모든 시스템에서 발생하는 것은 아니기 때문에, 케이스 바이 케이스로 실증할 필요가 있습니다.원래 공간(포인트 수의 차원 포함)은 몇 개의 고유 [citation needed]벡터가 걸쳐 있는 공간으로 축소되었습니다(데이터 손실이 있지만 가장 중요한 분산을 유지하는 것이 바람직합니다).

NMF(Non--negative Matrix Factoration(NMF)

주요 기사: 음이 아닌 행렬 인수분해

NMF는 음이 아닌 행렬을 음이 아닌 두 행렬의 곱으로 분해합니다.[9][10] 이는 천문학처럼 음이 아닌 신호만 [7][8]존재하는 분야에서 유망한 도구였습니다.NMF 잘 리 및이 곱셈 업데이트 규칙부터 알려져 있Seung,[7]하고 있는 지속적으로 개발되:포함 uncertainties,[9]의 배려의 손실 데이터와 병열 computation,[11]순차 construction[11]는 것은 안정성과 선형성의 NMF,[10]뿐만 아니라 다른 업데이트를 포함한 처리 전화가 왔어요디지털 imag에 데이터e 처리.[12]

건설 중 안정적인 성분 기반과 선형 모델링 과정을 통해 순차적[11] NMF는 특히 별 주위의 원반을 직접 촬영하기 위한 외부행성을 검출하는 방법 중 하나로 [10]천문학에서 별 주위의 구조를 직접 촬영할 때 플럭스를 보존할 수 있다.PCA와 비교하여 NMF는 매트릭스의 평균을 제거하지 않으며, 이는 비물리적 비음성 플럭스로 이어집니다. 따라서 NMF는 Ren [10]등이 증명한 것처럼 PCA보다 더 많은 정보를 보존할 수 있습니다.

커널 PCA

주요 기사: 커널 주성분 분석

주성분 분석은 커널 트릭에 의해 비선형 방식으로 사용될 수 있다.결과 기법은 데이터의 분산을 최대화하는 비선형 매핑을 구성할 수 있습니다.그 결과 발생하는 기술을 커널 PCA라고 합니다.

그래프 기반 커널 PCA

다른 눈에 띄는 비선형 기술에는 Isomap, 국소 선형 매립([13]LLE), Hessian LLE, Laplacian 고유 맵 및 접선 공간 [14][15]분석에 기반한 방법과 같은 다양체 학습 기술이 포함된다.이러한 기술은 데이터의 로컬 속성을 유지하는 비용 함수를 사용하여 저차원 데이터 표현을 구성하며 커널 PCA를 위한 그래프 기반 커널을 정의하는 것으로 볼 수 있습니다.

최근에는 고정 커널을 정의하는 대신 반확정 프로그래밍을 사용하여 커널을 학습하는 기술이 제안되었다.이러한 기술의 가장 두드러진 예는 최대 분산 전개(MVU)입니다.MVU의 중심 아이디어는 (내부 제품 공간에서) 가장 가까운 이웃들 사이의 모든 쌍별 거리를 정확하게 유지하면서 가장 가까운 이웃들이 아닌 점들 사이의 거리를 최대화하는 것이다.

근린보존에 대한 대안적 접근법은 입력공간과 출력공간 사이의 거리 차이를 측정하는 비용함수를 최소화하는 것이다.그러한 기법의 중요한 예로는 PCA와 동일한 고전적인 다차원 스케일링, 데이터 공간에서 측지학적 거리를 사용하는 이소맵, 데이터 공간에서 확산 거리를 사용하는 확산 맵, 쌍에 걸친 분포 간의 차이를 최소화하는 t-분산 확률적 인접 임베딩(t-SNE) 등이 있다.그리고 곡선 성분 분석.

비선형 차원 축소에 대한 다른 접근법은 보틀넥 숨겨진 레이어가 [16]있는 특수한 피드포워드 뉴럴 네트워크인 자동 인코더를 사용하는 것이다.딥 인코더의 훈련은 일반적으로 탐욕적인 레이어별 사전 훈련(예: 제한된 볼츠만 기계 스택 사용)을 사용하여 수행되며, 그 후 역전파에 기초한 미세 조정 단계가 뒤따른다.

2D 점 세트에 대한 결과 LDA 투영을 시각적으로 표현한 것입니다.

선형 판별 분석(LDA)

주요 기사 : 선형 판별 분석

선형 판별 분석(LDA)은 피셔의 선형 판별 분석의 일반화로서, 통계, 패턴 인식 및 기계 학습에서 두 개 이상의 객체 또는 이벤트의 클래스를 특성화하거나 분리하는 기능의 선형 조합을 찾는 데 사용됩니다.

일반 판별 분석(GDA)

GDA는 커널 함수 연산자를 이용한 비선형 판별 분석을 다룬다.기본 이론은 GDA 방법이 입력 벡터를 고차원 피쳐 [17][18]공간에 매핑하는 한 SVM(support-vector machine)에 가깝습니다.LDA와 마찬가지로 GDA의 목적은 클래스 간 산란 대 클래스 내 산란 비율을 최대화하여 더 낮은 차원 공간에 대한 특징에 대한 투영을 찾는 것이다.

자동 인코더

주요 기사:자동 인코더

자동 인코더는 부호화에서 원래 표현까지의 역함수와 함께 비선형 치수 축소 함수 및 부호화를 학습하기 위해 사용할 수 있다.

t-SNE

주요 기사: t-분포 확률적 인접 매입

T-분산 확률 인접 임베딩(t-SNE)은 고차원 데이터 세트의 시각화에 유용한 비선형 차원 축소 기법이다.클러스터링이나 특이치 검출 등의 분석에는 사용하지 않는 것이 좋습니다.밀도와 거리가 반드시 [19]잘 유지되는 것은 아니기 때문입니다.

UMAP

주요 기사:균일한 매니폴드 근사 및 투영

균일 매니폴드 근사 및 투영(UMAP)은 비선형 치수 감소 기법입니다.시각적으로는 t-SNE와 비슷하지만, 데이터가 국소적으로 연결된 리만 다양체에 균일하게 분포되어 있고 리만 메트릭이 국소적으로 일정하거나 거의 국소적으로 일정하다고 가정한다.

치수 축소

고차원 데이터 세트(즉, 10개 이상의 치수)의 경우,[20] 차원 저주의 영향을 피하기 위해 일반적으로 K-근접 이웃 알고리즘(k-NN)을 적용하기 전에 차원 축소가 수행된다.

특징 추출과 차원 축소는 전처리 단계로서 주성분 분석(PCA), 선형 판별 분석(LDA), 표준 상관 분석(CCA), 또는 NMF(non-negative matrix factorization) 기술을 사용하여 한 단계로 결합할 수 있으며, 이어서 축소 차원 공간에서의 특징 벡터에 대한 K-NN에 의한 클러스터링이 이루어진다.기계학습에서는 이 과정을 저차원 [21]매립이라고도 합니다.

very-high-dimensional 데이터 셋을 들어(예를 들어 때 라이브 비디오 스트림, DNA나high-dimensional 시간 시리즈에 유사성 검색을 수행하는)은 VLDB 회의 도구 상자에서locality-sensitive 해시, 무작위 projection,[22]"스케치"[23]또는 다른high-dimensional 유사 검색 기법을 사용하여 빠른 대략적인 K-NN 검색을 실행하는 t. 수 있그가 겨우실행 가능한 옵션

적용들

신경과학에서 가끔 사용되는 차원 축소 기법은 가능한 한 많은 원본 데이터에 대한 정보가 보존되도록 데이터셋의 저차원적 표현을 찾는 최대 정보 [citation needed]차원입니다.

「 」를 참조해 주세요.

추천 시스템
개념
방법과 과제
실장
조사.

메모들

  1. ^ a b van der Maaten, Laurens; Postma, Eric; van den Herik, Jaap (October 26, 2009). "Dimensionality Reduction: A Comparative Review" (PDF). J Mach Learn Res. 10: 66–71.
  2. ^ Pudil, P.; Novovičová, J. (1998). "Novel Methods for Feature Subset Selection with Respect to Problem Knowledge". In Liu, Huan; Motoda, Hiroshi (eds.). Feature Extraction, Construction and Selection. p. 101. doi:10.1007/978-1-4615-5725-8_7. ISBN 978-1-4613-7622-4.
  3. ^ Rico-Sulayes, Antonio (2017). "Reducing Vector Space Dimensionality in Automatic Classification for Authorship Attribution". Revista Ingeniería Electrónica, Automática y Comunicaciones. 38 (3): 26–35. ISSN 1815-5928.
  4. ^ Samet, H. (2006) 다차원 및 미터법 데이터 구조의 기초.모건 카우프만입니다ISBN 0-12-369446-9
  5. ^ C. 딩, X.H. Zha, H.D. Simon, Adaptive Dimension Reduction for Clustering High Dimension Data, Proceedings of International Conference on Data Mining, 2002
  6. ^ Lu, Haiping; Plataniotis, K.N.; Venetsanopoulos, A.N. (2011). "A Survey of Multilinear Subspace Learning for Tensor Data" (PDF). Pattern Recognition. 44 (7): 1540–1551. doi:10.1016/j.patcog.2011.01.004.
  7. ^ a b Daniel D. Lee & H. Sebastian Seung (1999). "Learning the parts of objects by non-negative matrix factorization". Nature. 401 (6755): 788–791. Bibcode:1999Natur.401..788L. doi:10.1038/44565. PMID 10548103. S2CID 4428232.
  8. ^ Daniel D. Lee & H. Sebastian Seung (2001). Algorithms for Non-negative Matrix Factorization (PDF). Advances in Neural Information Processing Systems 13: Proceedings of the 2000 Conference. MIT Press. pp. 556–562.
  9. ^ a b Blanton, Michael R.; Roweis, Sam (2007). "K-corrections and filter transformations in the ultraviolet, optical, and near infrared". The Astronomical Journal. 133 (2): 734–754. arXiv:astro-ph/0606170. Bibcode:2007AJ....133..734B. doi:10.1086/510127. S2CID 18561804.
  10. ^ a b c d Ren, Bin; Pueyo, Laurent; Zhu, Guangtun B.; Duchêne, Gaspard (2018). "Non-negative Matrix Factorization: Robust Extraction of Extended Structures". The Astrophysical Journal. 852 (2): 104. arXiv:1712.10317. Bibcode:2018ApJ...852..104R. doi:10.3847/1538-4357/aaa1f2. S2CID 3966513.
  11. ^ a b c Zhu, Guangtun B. (2016-12-19). "Nonnegative Matrix Factorization (NMF) with Heteroscedastic Uncertainties and Missing data". arXiv:1612.06037 [astro-ph.IM].
  12. ^ Ren, Bin; Pueyo, Laurent; Chen, Christine; Choquet, Elodie; Debes, John H.; Duechene, Gaspard; Menard, Francois; Perrin, Marshall D. (2020). "Using Data Imputation for Signal Separation in High Contrast Imaging". The Astrophysical Journal. 892 (2): 74. arXiv:2001.00563. Bibcode:2020ApJ...892...74R. doi:10.3847/1538-4357/ab7024. S2CID 209531731.
  13. ^ Roweis, S. T.; Saul, L. K. (2000). "Nonlinear Dimensionality Reduction by Locally Linear Embedding". Science. 290 (5500): 2323–2326. Bibcode:2000Sci...290.2323R. CiteSeerX 10.1.1.111.3313. doi:10.1126/science.290.5500.2323. PMID 11125150.
  14. ^ Zhang, Zhenyue; Zha, Hongyuan (2004). "Principal Manifolds and Nonlinear Dimensionality Reduction via Tangent Space Alignment". SIAM Journal on Scientific Computing. 26 (1): 313–338. doi:10.1137/s1064827502419154.
  15. ^ Bengio, Yoshua; Monperrus, Martin; Larochelle, Hugo (2006). "Nonlocal Estimation of Manifold Structure". Neural Computation. 18 (10): 2509–2528. CiteSeerX 10.1.1.116.4230. doi:10.1162/neco.2006.18.10.2509. PMID 16907635. S2CID 1416595.
  16. ^ Hongbing Hu, Stephen A. Zahorian, (2010) "HMM 음성 인식을 위한 차원 감소 방법", ICASSP 2010, 댈러스, 텍사스 주
  17. ^ Baudat, G.; Anouar, F. (2000). "Generalized Discriminant Analysis Using a Kernel Approach". Neural Computation. 12 (10): 2385–2404. CiteSeerX 10.1.1.412.760. doi:10.1162/089976600300014980. PMID 11032039. S2CID 7036341.
  18. ^ Haghighat, Mohammad; Zonouz, Saman; Abdel-Mottaleb, Mohamed (2015). "CloudID: Trustworthy cloud-based and cross-enterprise biometric identification". Expert Systems with Applications. 42 (21): 7905–7916. doi:10.1016/j.eswa.2015.06.025.
  19. ^ Schubert, Erich; Gertz, Michael (2017). Beecks, Christian; Borutta, Felix; Kröger, Peer; Seidl, Thomas (eds.). "Intrinsic t-Stochastic Neighbor Embedding for Visualization and Outlier Detection". Similarity Search and Applications. Lecture Notes in Computer Science. Cham: Springer International Publishing. 10609: 188–203. doi:10.1007/978-3-319-68474-1_13. ISBN 978-3-319-68474-1.
  20. ^ 케빈 베이어, 조나단 골드스타인, 라구 라마크리슈난, 우리샤프트(1999년) "가장 가까운 이웃"은 언제 의미가 있을까?데이터베이스 이론:ICDT99, 217–235
  21. ^ Shaw, B.; Jebara, T. (2009). "Structure preserving embedding" (PDF). Proceedings of the 26th Annual International Conference on Machine Learning – ICML '09. p. 1. CiteSeerX 10.1.1.161.451. doi:10.1145/1553374.1553494. ISBN 9781605585161. S2CID 8522279.
  22. ^ Bingham, E.; Mannila, H. (2001). "Random projection in dimensionality reduction". Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining – KDD '01. p. 245. doi:10.1145/502512.502546. ISBN 978-1581133912. S2CID 1854295.
  23. ^ Shasha, D High (2004) 타임 시리즈 베를린에서의 퍼포먼스 디스커버리: Springer.ISBN 0-387-00857-8

레퍼런스

외부 링크