초급 모드

이 섹션은 확인을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2022년 8월) (이 템플릿메시지를 삭제하는 방법과 타이밍에 대해 알아보기)

기본^[1] 모드는 안정된 상태를 유지할 수 있는 생화학적 네트워크를 통해 실현 가능한 최소한의 흐름 패턴으로 간주할 수 있습니다.이는 기본 모드를 더 단순한 경로로 분해할 수 없음을 의미한다.네트워크를 통과하는 모든 가능한 흐름은 기본 모드의 선형 조합에서 구성할 수 있습니다.

특정 네트워크의 기본 모드 세트는 고유합니다(임의 스케일링 팩터까지).고유성 및 비분해성과 관련된 기본 모드의 기본적 성질을 감안할 때, "패스웨이"라는 용어는 기본 모드로 정의될 수 있다.한 세포 상태에서 다른 세포 상태로 전환되는 동안 발현된 효소 세트가 변화함에 따라 기본 모드의 집합이 변경됩니다.수학적으로 기본 모드 집합은 정상 상태 조건을 만족시키는 플럭스 벡터 $집합{\displaystyle \mathbf{}}$ v$\$로 정의됩니다.

$\displaystyle \mathbf {N} \mathbf {v} (\mathbf {x} ,\mathbf {p} )=0}$

$여기$서$$N(\$displaystyle \mathbf {N})$은 화학측정 행렬,$v{\displaystyle \mathbf{}}$(\$displaystyle \mathbf {v})$는 비율 벡터,$x{\displaystyle \mathbf{}}$(\$displaystyle \mathbf {x}$는 정상 상태 부동(또는 내부) 종의 벡터, $(\$는 시스템 파라미터의 fector)이다$.$

중요한 조건은 각 불가역 반응의 속도가 음이 아닌 $vi{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle r_{}0}$0({$displaystyle \mathbf {v}_{irr}\geq$0$\})$이어야 한다는 것입니다.

보다 공식적인 정의는 다음과 같습니다.^[2]

기본 모드 ${\displaystyle \mathbf {v} _{$i$\}\}$는 플럭스의 벡터${\displaystyle {}_{}{}_{}}$, $…(\displaystyle v_{1$},$v_{$2},\$ldots$로 정의되어 다음 기준에 나열된 세 가지 조건을 충족합니다.

1. ${\displaystyle$ \$mathbf {v} _{i$}} 벡터는 ${\displaystyle N{\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ $=$ {\$displaystyle \mathbf {N}$ \$mathbf {v} _{i$}=$0$ 즉 정상 상태 조건을 충족해야 합니다.
2. 되돌릴 수 없는 모든 반응의 경우: $v{\displaystyle {}_{}}$ ${\displaystyle i_{}0}$0 { $displaystyle v$_ { $i$} \ $geq$ 0$$}즉, 모든 흐름 패턴은 가장 자연스러운 방향으로 진행되는 반응을 사용해야 합니다.이것은 기초 모드에 의해 설명되는 경로를 열역학적으로 실현 가능한 경로로 만든다.
3. $벡터{\displaystyle {\mathbf{}}_{}}$ $(\displaystyle$ \$mathbf$ {$v} _{$i$$})는 기본 값이어야 합니다.즉, $\$에서 0이 아닌 엔트리로 나타나는 동일한 효소 세트를 사용하여 첫 번째 및 두 번째 요건을 충족하는 다른 두 개의 벡터를 결합하여 $\$를 $생성$할 수 없습니다. 즉,${$를 정상 상태를 유지할 수 있는 다른 두 가지 경로로 분해할 수 $없습니다{\displaystyle {\mathbf{}}_{}}$.이것을 요소라고 합니다.보다 공식적인 테스트는 $(\$의 반응만을 포함하는 N$(\$의 서브매트릭스의 null 공간이 1차원이며 ^[2]엔트리가 0이 아니라는 것이다.

예

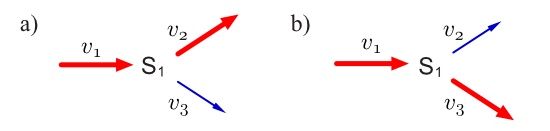
세 단계를 모두 되돌릴 수 없는 단순한 분기 경로를 고려합니다.이러한 경로에는 두꺼운(또는 빨간색) 반응 라인으로 표시된 두 가지 기본 모드가 허용된다.

${\displaystyle {v2\mathrm{}}_{}}$$({$ $v_$${$$2$}})와$v3({displaystyle$ v_{3})는 둘 다 되돌릴 수 없고, 둘 다 기본 모드는 열역학적 방향에 반하는 하나의 반응을 의미하기 때문에 불가능합니다.이 시스템의 각 모드는 위에서 설명한 세 가지 조건을 충족합니다.첫 번째 조건은 정상 상태, 즉 각 ${\displaystyle {}_{}}$ v\$displaystyle \mathbf {v}$ _{$i$에 대해 ${\displaystyle N{\mathbf{}}_{}}$ ${\displaystyle {}_{}}$$$$=$ ${\displaystyle 0}$ ${\displaystyle \mathbf {N}$ \$mathbf {v} _{i$}=$0$인 $것$이어야 합니다.

대수적으로 두 가지 모드는 다음과 같이 제공됩니다.

${\displaystyle \mathbf {v} _{1}=param {bmatrix}1\\1\\0\end{bmatrix}\param \mathbf {v}_{2}=param {bmatrix}1\0\1\end{bmatrix}$

이러한 각 벡터를 ${\displaystyle N{\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ i $=$ {\$displaystyle \mathbf {N}$ \$mathbf {v} _{i$}=$0$으)로 대입하면 조건 1이 충족되었음을 쉽게 알 수 있다.조건 2의 경우, 우리는 되돌릴 수 없는 모든 반응이 기본 모드의 해당 요소에서 양의 엔트리를 가지고 있는지 확인해야 한다.브런치 내의 3가지 반응은 모두 되돌릴 수 없고, 초등 모드의 모든 엔트리가 양의 것이므로 조건 2가 충족됩니다.

마지막으로 조건 3을 만족시키기 위해 2개의 기본 모드를 기본 모드에서 0이 아닌 동일한 엔트리를 사용하면서 안정된 상태를 유지할 수 있는 다른 경로로 분해할 수 있는지 여부를 확인해야 합니다.이 예에서는 정상 상태를 유지하는 기능을 중단하지 않고는 기본 모드를 더 이상 분해할 수 없습니다.따라서 세 가지 조건이 모두 충족되면 위의 두 벡터는 기본 모드라고 결론을 내릴 수 있습니다.

네트워크를 통과할 수 있는 모든 흐름은 기본 모드의 선형 조합으로 구성할 수 있습니다.즉, 다음과 같습니다.

${\displaystyle {displaystyle} \mathbf {v} &= \sum \mathbda _{i} \\mbox {where} \ \ \ \ mbox { where } \ \ \ \ \ mathbf { aligned } }$

네트워크를 통과하는 흐름의 전체 공간을 설명할 수 있습니다.$§$ $i\displaystyle$ \$displayda _{$i$$}}은(는) 0보다 크거나 같아야 합니다.반대할 수 없는 스텝이 실수로 역방향으로 진행되지 않도록 합니다.예를 들어 분기 경로에서 생각할 수 있는 정상 상태 흐름은 다음과 같습니다.

$({displaystyle v=2.5gc{bmatrix}1\\1\\0\end{bmatrix}}+0).5gc{bmatrix}1\\0\1\end{bmatrix}=gc{bmatrix}3.0\\2.5\\0.5\end{bmatrix}}$

단순 분기 경로의 유출 단계 중 하나가 가역화되면 두 유출 지점 간의 흐름을 나타내는 추가 기본 모드를 사용할 수 있게 된다.스케일링 팩터 "$\$는 음수일 수 없기 때문에 처음 2개의 모드만으로 2개의 브랜치 간의 플로우를 나타낼 수 없기 때문에 추가 모드가 나타납니다.

경로의 정의

Wikipedia 페이지 Metabrate path(대사 경로)는 경로를 "대사 경로는 세포 내에서 일어나는 일련의 화학 반응"으로 정의한다.이것은 어떤 일련의 반응도 대사 경로로 분류될 수 있다는 것을 의미한다.그러나 신진대사가 밝혀짐에 따라 해당과정, 크렙스 사이클 또는 세린 생합성 등과 같은 특정 라벨이 반응 그룹에 할당되었다.대부분의 경우 분류는 공통의 화학작용 또는 입력과 출력의 식별에 기초했다.예를 들어, 세린 생합성은 3-포스포글리세린산염에서 시작하여 세린에서 끝난다.이는 특히 경로가 동적 구조인 경우 유전자 발현에 환경적 결과로 변화하는 경로를 정의하기 위한 다소 임시 수단이다.예를 들어, 크레브 사이클은 교과서에 설명된 것처럼 순환적이지 않은 경우가 많습니다.대장균과 다른 박테리아에서는 아세테이트나 지방산의 ^[3]유산소 성장 중에만 순환한다.대신 혐기성 이하에서 효소는 숙시닐-CoA와 α-케토글루타르산염을 생성하는 두 개의 뚜렷한 생합성 경로로 기능한다.

따라서 경로를 단일 기본 모드 또는 일부 기본 모드의 조합으로 정의하는 것이 제안되었다^[4].추가된 장점은 기본 모드 세트가 고유하고 단순한 경로로 분해할 수 없다는 것이다.따라서 단일 기본 모드는 기본 경로로 간주할 수 있습니다.한 세포 상태에서 다른 세포 상태로 전환되는 동안 발현된 효소 세트가 변화함에 따라 기본 모드의 집합이 변경됩니다.

따라서 기본 모드는 경로에 대한 명확한 정의를 제공합니다.

조건 3에 대한 코멘트

조건 3은 초등 모드의 비분해성과 관련되며, 이것이 초등 모드의 관심을 끄는 부분이기도 하다.앞에서 설명한 것처럼 다른 두 가지 중요한 특징은 경로의 고유성과 열역학적 신뢰성입니다.분해는 모드를 두 개 이상의 다른 모드의 조합으로 나타낼 수 있음을 의미합니다.$예$를 들어 모드 $(\$은 $(\$ _${2})$와 $(\$ _${3$의 두 가지 다른 모드로 구성할 수 있습니다.

${\displaystyle \mathbf {e} _{1} \mathbf {e} _{2} + \mathbf {e} _{3}$

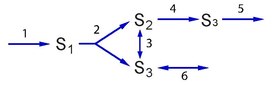
모드를 분해할 수 있다는 것은 모드가 초급 모드가 아님을 의미합니까?조건 3은 분해가 특정 모드가 기본 모드인지 여부를 결정하는 규칙을 제공합니다.해당 모드에서 사용되지 않는 효소를 도입하여 특정 모드를 분해하는 것만이 가능한 경우 해당 모드는 기본 모드입니다.즉, 현재 모드에서 사용되는 효소로 경로(즉, 안정된 상태를 유지할 수 있는 것)를 생성하는 방법이 하나 이상 있는가?이 경우 모드는 기본 모드가 아닙니다.이 미묘한 상태를 설명하기 위해 아래 표시된 경로를 고려하십시오.

이 경로는 해당과정의 정형화된 표현을 나타낸다.3단계 및 6단계는 가역성이 있으며 각각 트리오스인산 이성질화효소 및 글리세롤 3-인산탈수소효소에 해당한다.

네트워크에는 4개의 기본 플럭스모드가 있습니다.이러한 모드는 아래 그림에 나타나 있습니다.

기본 플럭스 모드 벡터는 다음과 같습니다.

${n1}:{pq}:{p}:{n1}:{n1}:{n2}}:{n2}}:{n2}}:{n2}}:{Num}:{n2} {: 1&{p;{-}:{-&{-&{namp;{p;{p;{-}:0}:0}:0}:0:{-}1&{\facebook {-}0&{\facebook {-}}2&{\facebook {-}}1&{\facebook {-}}0&{\facebook {-}}1&{\facebook {-}}1&{-}1&{\facebook {-}}{-}}}}1&{\facebook {-}}{-}}{-}}}}{\facebook {-}}}}{-}}}}}}}{\facebook {-$

기본 모드 세트에 음의 엔트리가 있는 것은, 이러한 엔트리가 가역 스텝에 대응하고 있기 때문입니다.주목되는 것은 제4 벡터 ${\displaystyle \mathrm{e4}}$ $=$ ${\displaystyle [}$ ${\displaystyle \text{1}\mathrm{}}$ ${\displaystyle \text{1}\mathrm{}}$ 0 ${\displaystyle \text{1}\mathrm{}}$ 1${\displaystyle {}^{}}$]${\displaystyle T^{}}${\$display e_{4$}=[$1\$1\ 0$\ 1\$1$\$ ]^{$T}($$여기$서$$T {\$display T}$는 전치)가 제1 및 제2 벡터의 합에서 형성될 수 있다는 관측이다.이는 네 번째 벡터가 기본 모드가 아님을 나타냅니다.

$\displaystyle \mathbf {e} _{\display {bmatrix} {\display {-}} \{\display {-}} {-}} \ {\display {-} {-}} {-}} {-}} {-}} {-}} {-}}} {-}} {-}}}} {-} {-}}}}: {\\displaystylash {-} {-} {-}}} {-}}}} {-} {-} {-}}}}}}}}}{-}\{\matrix {-}}\{\matrix {-}}\{\matrix {-}}\{\matrix}\\\\mathbf {e}_{\matrix}+{\matrix}_{\matrix}\matrix}\matrix {-}\matrix}\{-}\matrix}\matrix}\mat {-}\matrix}\mat {-}}}\mat {-}: {-}}\matrix}\matrix}{-}{-{-}}\\end {bmatrix}}$

단, 이 분해는 $(\$ _${4$에는 사용되지 않는 새로운 $효소{\displaystyle {}_{}}$ $(\$를 도입했기 때문에만 작동합니다.실제로 $($기본 모드에서 사용되는 ${\displaystyle {e1\mathrm{}}_{}}$ ${\displaystyle {e2\mathrm{}}_{}}$ ${\displaystyle {e4\mathrm{}}_{}}$ ${\displaystyle \text{e5}{}_{}}$, $($ e_${1}, e_{2}, e_{4}, e_{5}\mbox{and}}\{6$의 5단계만으로 e4($표시$ 스타일 $\mathbf {e}_{4})$를 정상 상태를 유지할 수 있는 경로로 $분해$하는 것은 불가능합니다.따라서 e $(\$는 초급 모드라고 결론짓습니다.

「 」를 참조해 주세요.

• 계산 시스템 생물학
• 대사조절분석
• 대사망
• 대사 경로
• 메타노믹스

레퍼런스