익스텐더블 해싱

Extendable 해싱은 해시를 비트 문자열로 처리하고 버킷 조회 시 트라이어를 사용하는 해시 시스템의 일종이다.^[1]시스템의 계층적 특성 때문에 재해싱은 증분 연산(필요에 따라 버킷을 한 번에 하나씩 수행)이다.즉, 시간에 민감한 애플리케이션은 표준 전체 테이블 재시도에 비해 테이블 증가의 영향을 덜 받는다는 것을 의미한다.

확장 가능한 해싱은 1979년 로널드 파긴에 의해 설명되었다.사실상 모든 최신 파일 시스템은 확장 가능한 해싱 또는 B-tree를 사용한다.특히 Global File System, ZFS 및 SpadFS 파일 시스템은 확장 가능한 해싱을 사용한다.^[2]

예

해시 함수 h (${\displaystyle k}$ )${\displaystyle h(k)}$이(가) 비트 문자열을 반환한다고$$ 가정하십시오.각 문자열의 첫 번째 i비트는 "디렉토리"(해시 테이블)에서 그것들이 어디로 갈지 알아내는 인덱스로 사용될 것이다.또한 표에 있는 모든 항목의 색인이 고유할 정도로 나는 가장 작은 숫자다.

사용할 키:

${\displaystyle {\progress}h(k_{1})=100100\\\h(k_{2})=010110\h(k_{3})=110\end{aigned}}}}}}$

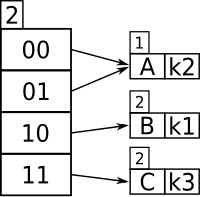
이 특정 예제의 경우 버킷 크기가 1이라고 가정해 봅시다.처음 삽입되는 두 개의 키(k와₁ k₂)는 가장 중요한 비트로 구별할 수 있으며 다음과 같이 표에 삽입된다.

이제, 만약₃ k를 테이블로 해시한다면, 세 개의 키를 모두 1비트(k와 k 모두 1을 그들의 가장 왼쪽₃ 비트로₁ 가지고 있기 때문에)로 구별하기에는 충분하지 않을 것이다.또한, 버킷 크기가 하나이기 때문에 테이블이 넘칠 것이다.처음 두 개의 가장 중요한 비트를 비교하면 각 키에 고유한 위치를 제공할 수 있기 때문에 디렉토리 크기는 다음과 같이 두 배가 된다.

그래서 이제 k와₁ k는₃ 처음 두 개의 왼쪽 비트로 구별되는 독특한 위치를 갖게 되었다.k는₂ 테이블의 위쪽 절반에 있기 때문에 0으로 시작하는 그것과 비교할 다른 키가 없기 때문에 00와 01 모두 그것을 가리킨다.

위의 예는 파긴 외 연구진(1979)에서 나온 것이다.

추가상세부

${\displaystyle h(k_{4}=011110}$

이제 k를₄ 삽입해야 하는데, 처음 두 비트는 01로 되어 있다.(1110), 그리고 디렉토리의 2비트 깊이를 사용하여 01에서 버킷 A로 매핑한다.버킷 A가 가득 찼으므로(최대 크기 1) 분할해야 하며, 버킷 A에 대한 포인터가 두 개 이상 있으므로 디렉토리 크기를 늘릴 필요가 없다.

필요한 것은 다음에 대한 정보다.

1. 디렉토리를 매핑하는 키 크기(전역 깊이)
2. 버킷을 이전에 매핑한 키 크기(로컬 깊이)

두 가지 조치 사례를 구별하기 위해:

1. 버킷이 가득 찰 때 디렉터리 배가
2. 새 버킷 생성 및 이전 버킷과 새 버킷 간에 항목 재분배

확장 가능한 해시 구조의 초기 사례를 살펴보면, 각 디렉토리 항목이 하나의 버킷을 가리킬 경우, 로컬 깊이는 글로벌 깊이와 같아야 한다.

디렉터리 항목 수는 2개^{global depth}, 초기 버킷 수는 2개다^{local depth}.

따라서 전역 깊이가 로컬 깊이 = 0이면 2⁰ = 1이므로 하나의 포인터로 된 초기 디렉터리가 하나의 버킷에 표시된다.

버킷이 가득 찬 경우 다음 두 작업 사례로 돌아가십시오.

1. 로컬 깊이가 글로벌 깊이와 같을 경우 버킷에 포인터가 하나만 있고 버킷에 매핑할 수 있는 다른 디렉터리 포인터가 없으므로 디렉터리를 두 배로 늘려야 한다.
2. 로컬 깊이가 글로벌 깊이보다 작으면 디렉터리에서 버킷으로 가는 포인터가 두 개 이상 존재하며 버킷을 분할할 수 있다.

키 01은 버킷 A를 가리키고 버킷 A의 로컬 깊이 1은 디렉터리의 전역 깊이 2보다 작으므로 버킷 A로 해싱된 키는 1비트 접두사(즉 0)만 사용했으며 버킷의 콘텐츠는 키 1 + 1 = 2비트를 사용하여 분할해야 한다. 일반적으로 d가 글로벌 깊이 D보다 작은 모든 로컬 깊이 d를 대상으로 한다.d는 버킷 분할 후 증가되어야 하며, 이전 버킷의 항목을 새 버킷으로 재배포하기 위해 각 항목 키의 비트 수로 사용되는 새로운 d.

지금

${\displaystyle h(k_{4}=011110}$

2비트 01..로 다시 시도되며, 이제 키 ${\displaystyle {01}_{}}$은 새 버킷을 가리키지만, 여전히$$ $k{\displaystyle {}_{}}$ 2 ${\$}}개가 들어 있으며(${\displaystyle {}_{}}$( ${\displaystyle {k\mathrm{}}_{}}$)${\displaystyle }$= ${\displaystyle 010110}$ ${\displaysty h(k_{2}=010110})$로 시작됨$$).

$k{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$}}개가$$ 키 00과 함께 000110이었다면, ${\displaystyle {k\mathrm{}}_{}}$ 2$${\$displaystyle k_{2$}}개는 새 버킷 A'에 남아 있었을 것이고$$, 버킷 D는 비어 있었을 것이기 때문에 문제가 없었을 것이다.

(이것은 버킷의 크기가 1보다 크고 새로 분할된 버킷이 넘치지 않는 한 모든 항목이 한 버킷에 다시 연결되지 않는 한, 지금까지 가장 가능성이 높은 경우였을 것이다.그러나 심층정보의 역할을 강조하기 위해서 그 예는 끝까지 논리적으로 추진될 것이다.)

따라서 버킷 D는 분할해야 하지만, 2인 로컬 깊이 확인은 글로벌 깊이인 2와 동일하므로, 충분한 세부사항(예: 3비트)의 키를 보유하기 위해서는 디렉토리를 다시 분할해야 한다.

1. 버킷 D는 꽉 차서 분리해야 한다.
2. D의 로컬 깊이 = 글로벌 깊이로서, 키의 비트 디테일을 증가시키려면 디렉토리가 두 배가 되어야 한다.
3. 디렉토리가 3으로 분할된 후 전역 깊이가 증가함
4. 새로운 엔트리 $k{\displaystyle {}_{}}$ ${\$는 글로벌 깊이 3비트로 다시 키핑되어$$ 국부 깊이 2가 있는 D로 종료되며, 현재 3으로 증가하여 D와 E로 분할할 수 있다.
5. 스플릿 버킷 D의 ${\displaystyle {내용}_{}}$인 k$$2 {\$displaystyle k_{$2}}개의 내용이 3비트로 재키팅되어 D'로 끝난다$.$
6. K4는 재시도되고 결국 스페어 슬롯이 있는 E로 끝난다.

Now, ${\displaystyle h(k_{2})=010110}$ is in D and ${\displaystyle h(k_{4})=011110}$ is tried again, with 3 bits 011.., and it points to bucket D which already contains ${\displaystyle k_{2}}$ so is full; D's local depth is 2 but now the global depth is 3 after the directory doubling, so now D can be split into bucket's D' and E, the contents of D, ${\displaystyle k_{2}}$ has its ${\displaystyle h(k_{2})}$ retried with a new global depth bitmask of 3 and ${\displaystyle k_{2}}$ ends up in D', then the new entry ${\displaystyle k_{4}}$ is retried with ${\displaystyle h(}$${\displaystyle k_{}}$ ${\displaystyle {4\mathrm{}}_{}}$) ${\displaystyle h(k_{4}}}$비트 마스크가$$ 3의 새로운 전역 깊이 비트 카운트를 사용하며 011이 제공되고 이 비트 마스크는 이제 비어 있는 새 버킷 E를 가리킨다.그래서 $k{\displaystyle {}_{}}$ ${\$는 버킷 E로 들어간다$$.

구현 예

아래는 Python의 확장 가능한 해싱 알고리즘으로 디스크 블록/메모리 페이지 연결, 캐싱 및 일관성 문제가 제거되었다.깊이가 정수의 비트 크기를 초과하면 디렉터리를 두 배로 늘리거나 버킷을 분할하면 항목이 다른 버킷으로 다시 삭제되지 않기 때문에 문제가 있다는 점에 유의하십시오.

코드는 최하위 비트를 사용하므로 전체 디렉토리를 하나의 블록으로 복사할 수 있어 테이블 확장이 더욱 효율적이다(Ramakrishnan & Gehrke(2003)).

파이톤 예

페이지_SZ = 10  계급 페이지:     반항하다 __init___(자아의) -> 없음:         자아의.지도를 그리다 = []         자아의.local_deep = 0      반항하다 가득 찬(자아의) -> 바가지 긁다:         돌아오다 렌(자아의.지도를 그리다) >= 페이지_SZ      반항하다 놓다(자아의, k, v) -> 없음:         을 위해 i, (핵심을, 가치를 매기다) 에 열거하다(자아의.지도를 그리다):             만일 핵심을 == k:                 굴을 파다 자아의.지도를 그리다[i]                 부숴뜨리다         자아의.지도를 그리다.덧셈을((k, v))      반항하다 얻다(자아의, k):         을 위해 핵심을, 가치를 매기다 에 자아의.지도를 그리다:             만일 핵심을 == k:                 돌아오다 가치를 매기다      반항하다 get_local_high_bit(자아의):       돌아오다 1 << 자아의.local_deep  계급 익스텐더블 해싱:     반항하다 __init___(자아의) -> 없음:         자아의.global = 0         자아의.전화번호부 = [페이지()]      반항하다 get_page(자아의, k):         h = 해시하다(k)         돌아오다 자아의.전화번호부[h & ((1 << 자아의.global) - 1)]      반항하다 놓다(자아의, k, v) -> 없음:         p = 자아의.get_page(k)         가득 찬 = p.가득 찬()         p.놓다(k, v)         만일 가득 찬:             만일 p.local_deep == 자아의.global:                 자아의.전화번호부 *= 2                 자아의.global += 1              p0 = 페이지()             p1 = 페이지()             p0.local_deep = p1.local_deep = p.local_deep + 1             high_bit = p.get_local_high_bit()             을 위해 k2, v2 에 p.지도를 그리다:                 h = 해시하다(k2)                 new_p = p1 만일 h & high_bit 다른 p0                 new_p.놓다(k2, v2)              을 위해 i 에 범위(해시하다(k) & (high_bit - 1), 렌(자아의.전화번호부), high_bit):                 자아의.전화번호부[i] = p1 만일 i & high_bit 다른 p0      반항하다 얻다(자아의, k):         돌아오다 자아의.get_page(k).얻다(k)  만일 __name__ == "__main__":     에 = 익스텐더블 해싱()     N = 10088     l = 리스트를 작성하다(범위(N))      수입하다 무작위의     무작위의.섞다(l)     을 위해 x 에 l:         에.놓다(x, x)     인쇄하다(l)      을 위해 i 에 범위(N):         인쇄하다(에.얻다(i)) 

메모들

참고 항목

• 트라이
• 해시 테이블
• 스테이블 해싱
• 일관된 해싱
• 선형 해싱

참조

• Fagin, R.; Nievergelt, J.; Pippenger, N.; Strong, H. R. (September 1979), "Extendible Hashing - A Fast Access Method for Dynamic Files", ACM Transactions on Database Systems, 4 (3): 315–344, doi:10.1145/320083.320092, S2CID 2723596
• Ramakrishnan, R.; Gehrke, J. (2003), Database Management Systems, 3rd Edition: Chapter 11, Hash-Based Indexing, pp. 373–378
• Silberschatz, Abraham; Korth, Henry; Sudarshan, S., Database System Concepts, Sixth Edition: Chapter 11.7, Dynamic Hashing

외부 링크

• 이 문서에는 NIST 문서의 공용 도메인 자료가 포함되어 있다.
• 아칸소 주립 대학교의 확장 가능한 해싱 노트
• 확장 가능한 해싱 노트
• 해시 기반 동적 지수에 대한 확장 가능한 해싱에 대한 데이터베이스 시스템 개념 도서 슬라이드