자유 스펙트럼 범위 (FSR )는 간섭계 또는 확산 광 소자 의 두 연속 반사 또는 전달 광 강도 최대치 또는 최소치 사이의 광 주파수 또는 파장 간격 이다.[1]
FSR은 항상 Δ ν {\displaystyle \Delta \nu Δ displaystyle \Delta \lambda } , 그 이유는 이러한 서로 다른 용어들이 각각 방출된 소스의 대역폭이나 선폭을 가리키기 때문이다.
일반적으로 일반적으로 공동의 자유 스펙트럼 범위(FSR)는 다음과 같다.
Δ λ FSR = 2 π L ( ∂ β ∂ λ ) − 1 {\displaystyle \left \Delta \lambda _{\text{ FSR}\오른쪽 ={\frac {2\pi }{L}\왼쪽({\frac {\partial \beta }{\partial \beta }{\partial \lambda }\오른쪽)^{-1} 또는 동등하게
Δ ν FSR = 2 π L ( ∂ β ∂ ν ) − 1 {\displaystyle \left \Delta \nu _{\text{ FSR}\오른쪽 ={\frac {2\pi }{L}\왼쪽({\frac {\partial \beta }{\partial \beta }{\partial \nu }\오른쪽)^{-1} 이러한 표현은 테일러 시리즈에서Δ β β 2 β \\displaystyle \Delta L=2\pi } Δ \\delta \beta } Here, β = k 0 n ( λ ) = 2 π λ n ( λ ) {\displaystyle \beta =k_{0}n(\lambda )={\frac {2\pi }{\lambda }}n(\lambda )} k 0 {\displaystyle k_{0}} λ {\displaystyle \lambda } n {\displaystyle n} 공동의 e 인덱스 및 L {\displaystyle L} displaystyle L}
Given that ( ∂ β ∂ λ ) = 2 π λ 2 [ n ( λ ) − λ ∂ n ∂ λ ] = 2 π λ 2 n g {\displaystyle \left \left({\frac {\partial \beta }{\partial \lambda }}\right)\right ={\frac {2\pi }{\lambda ^{2}}}\left[n(\lambda )-\lambda {\frac {\partial n}{\partial \lambda }}\right]={\frac {2\pi }{\lambda ^{2}}}n_{g }}},
Δ λ FSR = λ 2 n g L , {\displaystyle \Delta \lambda _{\text{ FSR}}={\frac {\lambda ^{2}}:{n_{\text{g}}} L}},} n g {\ displaystyle n_{\text{g}} 그룹 색인 이다또는 동등하게
Δ ν FSR = c n g L , {\displaystyle \Delta \nu _{\text{ FSR}={\frac {c}{n_{\text{g}}}} L}},} 여기서 c {\displaystyle c}
재료의 산포가 무시해도 될 정도라면(예: ∂n λ ≈ 0 displaystyle {\frac partial n}{\partial \lambda }}}\ 0 위
Δ λ FSR ≈ λ 2 n ( λ ) L , {\displaystyle \Delta \lambda _{\text{ FSR}}\ 약 {\frac {\lambda ^{2}}{n(\lambda )L},} 그리고
Δ ν FSR ≈ c n ( λ ) L . {\displaystyle \Delta \nu _{\text{ FSR}}\ 약 {\frac {c}{n(\lambda )L}. } FSR의 단순한 직관적인 해석은 왕복 시간 T R {\ 디스플레이 T_{R} .
T R = n g L c = 1 Δ ν FSR . {\displaystyle T_{R}={\frac {n_{\text{g}}} L}{c}}={\frac {1}{\Delta \nu _{\text{ FSR}}}.} 파장에서는 FSR이 에 의해 주어진다.
Δ λ FSR = λ 2 n g L , {\displaystyle \Delta \lambda _{\text{ FSR}}={\frac {\lambda ^{2}}:{n_{\text{g}}} L}},} 여기서 λ {\displaystyle \lambda } 아래에서 설명하는 Fabry-Pérot interferometer 와[3] L l {\displaystyle L=2l}, 여기 {\displaystyle L} l {\displaystyle l}
회절 그라팅 회절 그링 의 자유 스펙트럼 범위는 인접한 순서에서 동일한 범위와 겹치지 않는 주어진 순서에 대해 가장 큰 파장 범위다.(m + 1)번째 순서인 λ {\displaystyle \lambda } (λ Δ λ ){\displaystyle (\lambda +\Delta \lambda
Δ λ = λ m . {\displaystyle \Delta \lambda ={\frac {\lambda }{m}}. } 파브리-페로트 간섭계 Fabry-Pérot interferometer [3]
Δ λ = λ 0 2 2 n l cas θ + λ 0 ≈ λ 0 2 2 n l cas θ , {\displaystyle \delta \lambda ={\frac {\lambda _{0}}}}{2nl\cos \theta +\lambda _{0}}}}\cos \cos{2nl\cos \coses },},} 여기서 λ은0 가장 가까운 전송 피크의 중심 파장, n 굴절 지수 , , {\displaystyle \theta} {\displaystyle l} FSR은 파장 단위보다는 주파수로 인용되는 경우가 더 많다.
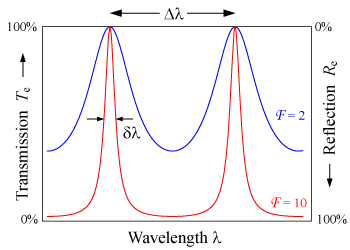
Δ f ≈ c 2 n l cas θ . {\displaystyle \Delta f\ 약 {\frac {c}{2nl\cos \theta}}. } 파장의 함수로서 에탈론의 전송. 하이파이네스 에탈론(빨간색 선)은 로우파이네스 에탈론(파란색)보다 더 날카로운 피크와 낮은 전송 미니마를 보여준다. 자유 스펙트럼 범위는 Δλ (그래프 위에 표시)이다.
FSR은 한 전송 대역 의 전체 너비 반최대 Δ³과 관련된다.
F = Δ λ δ λ = π 2 아크신 ( 1 / F ) , {\displaystyle {\mathcal{F}={\fraca \lambda }}{\delta \lambda }}}={\pi }{2\arcsin(1/{\sqrt{F})}},},},},} 여기서 F 4 R R 2 {\ displaystyle F={\frac {4R}{1-R)^{2 , R은 거울 의 반사율이다.
이 값은 일반적으로 (R > 0.5)에 의해 근사치된다.
F ≈ π F 2 = π R 1 / 2 ( 1 − R ) . {\displaystyle {\mathcal {F}\pi {\pi {\sqrt{F}}{2}}={\frac {\pi R^{1/2}}{(1-R)}}}}}}}}} } 참조 ^ Hecht, Eugene (2017). Optics (5th ed.). pp. 431–433, 614. ISBN 9780133977226 OCLC 953709783 . ^ Rabus, Dominik.G. (26 April 2007). Integrated Ring Resonators . ISBN 978-3-540-68788-7 OCLC 123893382 . ^ a b Ismail, N.; Kores, C. C.; Geskus, D.; Pollnau, M. (2016). "Fabry-Pérot resonator: spectral line shapes, generic and related Airy distributions, linewidths, finesses, and performance at low or frequency-dependent reflectivity" . Optics Express . 24 (15): 16366–16389. Bibcode :2016OExpr..2416366I . doi :10.1364/OE.24.016366 PMID 27464090 . 









 (서 있는 파형 공동의 경우 L
(서 있는 파형 공동의 경우 L![{\displaystyle \left|\left({\frac {\partial \beta }{\partial \lambda }}\right)\right|={\frac {2\pi }{\lambda ^{2}}}\left[n(\lambda )-\lambda {\frac {\partial n}{\partial \lambda }}\right]={\frac {2\pi }{\lambda ^{2}}}n_{g}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94bc7f13a49a62045f7002396deacd797e7fa47d)

 .또는 동등하게
.또는 동등하게
 (는) 진공에서 빛의 속도다.
(는) 진공에서 빛의 속도다. 





 공동의 길이.
공동의 길이. 


 발생 각도, l
발생 각도, l